/*
* Copyright (c)2015,煙台大學計算機與控制工程學院
* All rights reserved.
* 檔案名稱:項目4.cbp
* 作 者:朱希康
* 完成日期:2015年12月11日
* 版 本 号:v1.0
* 問題描述:Floyd算法
* 輸入描述:無
* 程式輸出:最小生成樹
*/
#ifndef GRAPH_H_INCLUDED
#define GRAPH_H_INCLUDED
#define MAXV 100 //最大頂點個數
#define INF 32767 //INF表示∞
typedef int InfoType;
//以下定義鄰接矩陣類型
typedef struct
{
int no; //頂點編号
InfoType info; //頂點其他資訊,在此存放帶權圖權值
} VertexType; //頂點類型
typedef struct //圖的定義
{
int edges[MAXV][MAXV]; //鄰接矩陣
int n,e; //頂點數,弧數
VertexType vexs[MAXV]; //存放頂點資訊
} MGraph; //圖的鄰接矩陣類型
//以下定義鄰接表類型
typedef struct ANode //弧的結點結構類型
{
int adjvex; //該弧的終點位置
struct ANode *nextarc; //指向下一條弧的指針
InfoType info; //該弧的相關資訊,這裡用于存放權值
} ArcNode;
typedef int Vertex;
typedef struct Vnode //鄰接表頭結點的類型
{
Vertex data; //頂點資訊
int count; //存放頂點入度,隻在拓撲排序中用
ArcNode *firstarc; //指向第一條弧
} VNode;
typedef VNode AdjList[MAXV]; //AdjList是鄰接表類型
typedef struct
{
AdjList adjlist; //鄰接表
int n,e; //圖中頂點數n和邊數e
} ALGraph; //圖的鄰接表類型
//功能:由一個反映圖中頂點鄰接關系的二維數組,構造出用鄰接矩陣存儲的圖
//參數:Arr - 數組名,由于形式參數為二維數組時必須給出每行的元素個數,在此将參數Arr聲明為一維數組名(指向int的指針)
// n - 矩陣的階數
// g - 要構造出來的鄰接矩陣資料結構
void ArrayToMat(int *Arr, int n, MGraph &g); //用普通數組構造圖的鄰接矩陣
void ArrayToList(int *Arr, int n, ALGraph *&); //用普通數組構造圖的鄰接表
void MatToList(MGraph g,ALGraph *&G);//将鄰接矩陣g轉換成鄰接表G
void ListToMat(ALGraph *G,MGraph &g);//将鄰接表G轉換成鄰接矩陣g
void DispMat(MGraph g);//輸出鄰接矩陣g
void DispAdj(ALGraph *G);//輸出鄰接表G
void Ppath(int path[][MAXV],int i,int j);
void Dispath(int A[][MAXV],int path[][MAXV],int n);
void Floyd(MGraph g);
#endif // GRAPH_H_INCLUDED
#include<stdio.h>
#include "head.h"
int main()
{
MGraph g;
int A[4][4]=
{
{0, 5,INF,7},
{INF,0, 4,2},
{3, 3, 0,2},
{INF,INF,1,0}
};
ArrayToMat(A[0], 4, g);
Floyd(g);
return 0;
}
#include <stdio.h>
#include <malloc.h>
#include "head.h"
//功能:由一個反映圖中頂點鄰接關系的二維數組,構造出用鄰接矩陣存儲的圖
//參數:Arr - 數組名,由于形式參數為二維數組時必須給出每行的元素個數,在此将參數Arr聲明為一維數組名(指向int的指針)
// n - 矩陣的階數
// g - 要構造出來的鄰接矩陣資料結構
void ArrayToMat(int *Arr, int n, MGraph &g)
{
int i,j,count=0; //count用于統計邊數,即矩陣中非0元素個數
g.n=n;
for (i=0; i<g.n; i++)
for (j=0; j<g.n; j++)
{
g.edges[i][j]=Arr[i*n+j]; //将Arr看作n×n的二維數組,Arr[i*n+j]即是Arr[i][j],計算存儲位置的功夫在此應用
if(g.edges[i][j]!=0 && g.edges[i][j]!=INF)
count++;
}
g.e=count;
}
void ArrayToList(int *Arr, int n, ALGraph *&G)
{
int i,j,count=0; //count用于統計邊數,即矩陣中非0元素個數
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
G->n=n;
for (i=0; i<n; i++) //給鄰接表中所有頭節點的指針域置初值
G->adjlist[i].firstarc=NULL;
for (i=0; i<n; i++) //檢查鄰接矩陣中每個元素
for (j=n-1; j>=0; j--)
if (Arr[i*n+j]!=0) //存在一條邊,将Arr看作n×n的二維數組,Arr[i*n+j]即是Arr[i][j]
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //建立一個節點*p
p->adjvex=j;
p->info=Arr[i*n+j];
p->nextarc=G->adjlist[i].firstarc; //采用頭插法插入*p
G->adjlist[i].firstarc=p;
}
G->e=count;
}
void MatToList(MGraph g, ALGraph *&G)
//将鄰接矩陣g轉換成鄰接表G
{
int i,j;
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
for (i=0; i<g.n; i++) //給鄰接表中所有頭節點的指針域置初值
G->adjlist[i].firstarc=NULL;
for (i=0; i<g.n; i++) //檢查鄰接矩陣中每個元素
for (j=g.n-1; j>=0; j--)
if (g.edges[i][j]!=0) //存在一條邊
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //建立一個節點*p
p->adjvex=j;
p->info=g.edges[i][j];
p->nextarc=G->adjlist[i].firstarc; //采用頭插法插入*p
G->adjlist[i].firstarc=p;
}
G->n=g.n;
G->e=g.e;
}
void ListToMat(ALGraph *G,MGraph &g)
//将鄰接表G轉換成鄰接矩陣g
{
int i,j;
ArcNode *p;
g.n=G->n; //根據一樓同學“舉報”改的。g.n未指派,下面的初始化不起作用
g.e=G->e;
for (i=0; i<g.n; i++) //先初始化鄰接矩陣
for (j=0; j<g.n; j++)
g.edges[i][j]=0;
for (i=0; i<G->n; i++) //根據鄰接表,為鄰接矩陣指派
{
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
g.edges[i][p->adjvex]=p->info;
p=p->nextarc;
}
}
}
void DispMat(MGraph g)
//輸出鄰接矩陣g
{
int i,j;
for (i=0; i<g.n; i++)
{
for (j=0; j<g.n; j++)
if (g.edges[i][j]==INF)
printf("%3s","∞");
else
printf("%3d",g.edges[i][j]);
printf("\n");
}
}
void DispAdj(ALGraph *G)
//輸出鄰接表G
{
int i;
ArcNode *p;
for (i=0; i<G->n; i++)
{
p=G->adjlist[i].firstarc;
printf("%3d: ",i);
while (p!=NULL)
{
printf("-->%d/%d ",p->adjvex,p->info);
p=p->nextarc;
}
printf("\n");
}
}
void Ppath(int path[][MAXV],int i,int j) //前向遞歸查找路徑上的頂點
{
int k;
k=path[i][j];
if (k==-1) return; //找到了起點則傳回
Ppath(path,i,k); //找頂點i的前一個頂點k
printf("%d,",k);
Ppath(path,k,j); //找頂點k的前一個頂點j
}
void Dispath(int A[][MAXV],int path[][MAXV],int n)
{
int i,j;
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (A[i][j]==INF)
{
if (i!=j)
printf("從%d到%d沒有路徑\n",i,j);
}
else
{
printf(" 從%d到%d=>路徑長度:%d 路徑:",i,j,A[i][j]);
printf("%d,",i); //輸出路徑上的起點
Ppath(path,i,j); //輸出路徑上的中間點
printf("%d\n",j); //輸出路徑上的終點
}
}
}
void Floyd(MGraph g)
{
int A[MAXV][MAXV],path[MAXV][MAXV];
int i,j,k;
for (i=0; i<g.n; i++)
for (j=0; j<g.n; j++)
{
A[i][j]=g.edges[i][j];
path[i][j]=-1;
}
for (k=0; k<g.n; k++)
{
for (i=0; i<g.n; i++)
for (j=0; j<g.n; j++)
if (A[i][j]>A[i][k]+A[k][j])
{
A[i][j]=A[i][k]+A[k][j];
path[i][j]=k;
}
}
Dispath(A,path,g.n); //輸出最短路徑
}
運作結果:
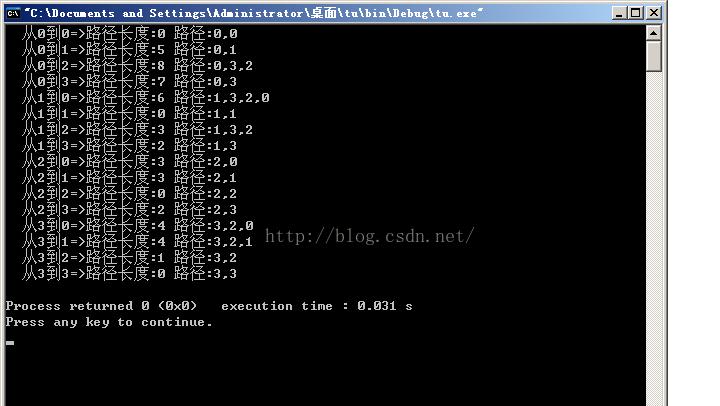
知識點總結:
1.從任意一條單邊路徑開始。所有兩點之間的距離是邊的權,如果兩點之間沒有邊相連,則權為無窮大。 2.對于每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比已知的路徑更短。如果是更新它。 把圖用鄰接矩陣G表示出來,如果從Vi到Vj有路可達,則G[i,j]=d,d表示該路的長度;否則G[i,j]=無窮大。定義一個矩陣D用來記錄所插入點的資訊,D[i,j]表示從Vi到Vj需要經過的點,初始化D[i,j]=j。把各個頂點插入圖中,比較插點後的距離與原來的距離,G[i,j] = min( G[i,j], G[i,k]+G[k,j] ),如果G[i,j]的值變小,則D[i,j]=k。在G中包含有兩點之間最短道路的資訊,而在D中則包含了最短通路徑的資訊。