文章目錄
-
-
- 遞歸與搜尋部分知識點小結
- 搜尋部分學習小結
- 背包問題知識總結
- 動态規劃部分知識點總結
- 貪心算法部分知識點
- 貪心算法部分題目及知識點總結
- 知識補充:
-
- 遞歸:
-
-
- 循環,疊代,遞推,遞歸的差別:
- 遞歸的三大元素(思路步驟):
- 遞歸的優化思路:
- 遞歸轉疊代:
-
- 動态規劃:
-
-
- 分治政策:
- 動态規劃:
- 動态規劃的三大步驟:
-
- 參考文章:
-
-
- 為什麼你學不會遞歸?告别遞歸,談談我的一些經驗
- 再談循環&疊代&回溯&遞歸&遞推這些基本概念
- 遞歸與疊代的差別
- 尾遞歸
- 尾調用優化
- 為什麼你學不過動态規劃?告别動态規劃,談談我的經驗
-
- 作業一:
-
-
- 數字三角形算法:
- 小朋友上台階(斐波那契數列):
- 輸油管道問題:
- 最大子段和問題:
- 0-1背包動态規劃:
- 背包問題的貪心算法:
- 木棒的加工:
- 魚塘釣魚問題:
-
- 實驗一:
-
-
- 楊輝三角形:
- 字元串對比:
- 攔截飛彈(LIS,貪心,動态規劃):
- 八(n)(2n)皇後問題:
-
- 實驗二:
-
-
- Fibonacci數列:
- 校門外的樹:
- 奪寶奇兵:
- 分解質因數:
-
- 寫在最後:
-
-
- 算法的學習有兩個困難的地方(參考文章:[算法之美(豆瓣讀書)](https://book.douban.com/review/1325850/)):
- 算法是一門很奇妙的課程,做算法需要靜下心來去堅持,隻有那樣才能發現其中的樂趣與美妙,才會有所收獲,加油!
-
-
遞歸與搜尋部分知識點小結
搜尋部分學習小結
背包問題知識總結
動态規劃部分知識點總結
貪心算法部分知識點
貪心算法部分題目及知識點總結
知識補充:
遞歸:
循環,疊代,遞推,遞歸的差別:
循環:不斷重複進行某一運算、操作。
疊代(A重複調用B):不斷對前一舊值運算得到新值直到達到精度。一般用于得到近似目标值,反複循環同一運算式(函數),并且總是把前一 次運算結果反代會運算式進行下一次運算
遞推:從初值出發反複進行某一運算得到所需結果。-----從已知到未知,從小到達(比如每年長高9cm,20年180,30後270)
回溯:遞歸時經曆的一個過程。
遞歸(A調用A):從所需結果出發不斷回溯前一運算直到回到初值再遞推得到所需結果----從未知到已知,從大到小,再從小到大(你想進bat,那麼程式設計就的牛逼,就得解除安裝玩者農藥,努力學習)。遞歸(Recursion)是從歸納法(Induction)衍生出來的。
遞歸的三大元素(思路步驟):
1、明确函數想要幹什麼
2、尋找遞歸結束條件
3、找出函數的等價關系式
注意:當我們第三步找出等價函數之後,還得再傳回去第二步,根據第三步函數的調用關系,看看會不會出現一些漏掉的結束條件(避免出錯或者死循環等問題(遞歸結束條件考慮的少,循環一直無法結束))。
遞歸的優化思路:
1.考慮是否有重複計算:當一個遞歸調用開始時,可能存在很多子問題的重複計算,這樣在做這些重複計算時會花費更多的時間,造成不必要的時間浪費,當然一個程式想要做到完美是非常困難的,我們也不可能超越程式應該有的時間複雜度和空間複雜度去直接給出結果,這裡對于時間的優化,我們給出以空間換取時間的思路,用備忘錄的方式去記錄那些可能存在重複計算的子問題的結果,當遇到已經計算出結果的子問題時,我們采取直接取出結果代替重複計算的方式去進行優化。
//設這裡遞歸函數的等價關系為f(n)=f(n-1)+f(n-2)
int f(int n){
if(n <= 1){
return n;
}
//先判斷有沒計算過(假定初始數組元素為-1)
if(arr[n] != -1){
//計算過,直接傳回
return arr[n];
}else{
// 沒有計算過,遞歸計算,并且把結果儲存到 arr數組裡
arr[n] = f(n-1) + f(n-2);
reutrn arr[n];
}
}
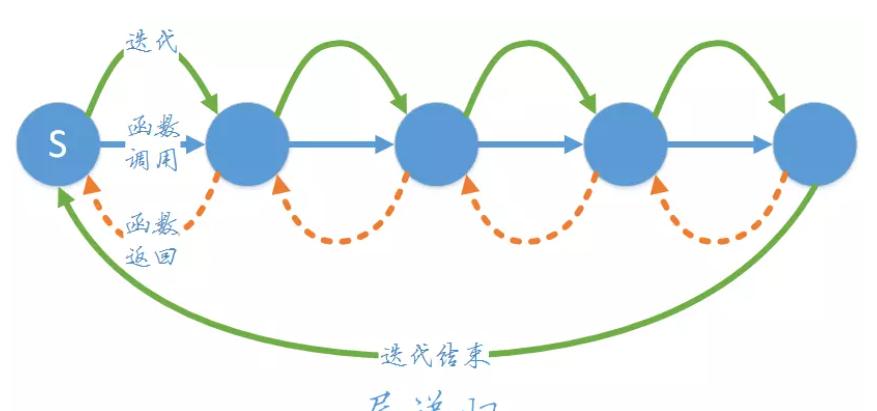
遞歸轉疊代:
理論上遞歸和疊代可以互相轉換,但實際從算法結構來說,遞歸聲明的結構并不總能轉換為疊代結構,即疊代可以轉換為遞歸,但遞歸不一定能轉換為疊代。一般來說能用疊代的就不用遞歸,遞歸調用函數,浪費空間,并且遞歸太深容易造成堆棧的溢出(尾遞歸可以解決堆棧的溢出,但是仍然避免不了函數調用的開銷)。
将遞歸算法轉換為非遞歸算法有兩種方法,一種是直接求值(疊代),不需要回溯;另一種是不能直接求值,需要回溯。前者使用一些變量儲存中間結果,稱為直接轉換法,後者使用棧儲存中間結果,稱為間接轉換法。
直接轉換法:
直接轉換法通常用來消除尾遞歸(tail recursion)和單向遞歸,将遞歸結構用疊代結構來替代。(單向遞歸 → 尾遞歸 → 疊代)
間接轉換法:
遞歸實際上利用了系統堆棧實作自身調用,我們通過使用棧儲存中間結果模拟遞歸過程,将其轉為非遞歸形式。
尾遞歸函數遞歸調用傳回時正好是函數的結尾,是以遞歸調用時就不需要保留目前棧幀,可以直接将目前棧幀覆寫掉。
//這是遞歸
int funcA(int n)
{
if(n > 1)
return n+funcA(n-1);
else
return 1;
}
//這是疊代
int funcB(int n)
{
int i,s=0;
for(i=1;i<n;i++)
s+=i;
return s;
}
對于尾調用、尾遞歸等概念可以參考以下文章:
尾遞歸
尾調用優化
動态規劃:
介紹動态規劃之前先介紹一下分治政策。
分治政策:
将原問題分解為若幹個規模較小但類似于原問題的子問題(Divide),「遞歸」的求解這些子問題(Conquer),然後再合并這些子問題的解來建立原問題的解。
因為在求解大問題時,需要遞歸的求小問題,是以一般用「遞歸」的方法實作,即自頂向下。
動态規劃:
動态規劃其實和分治政策是類似的,也是将一個原問題分解為若幹個規模較小的子問題,遞歸的求解這些子問題,然後合并子問題的解得到原問題的解。
差別在于這些子問題會有重疊,一個子問題在求解後,可能會再次求解,于是我們想到将這些子問題的解存儲起來,當下次再次求解這個子問題時,直接拿過來就是。
其實就是說,動态規劃所解決的問題是分治政策所解決問題的一個子集,隻是這個子集更适合用動态規劃來解決進而得到更小的運作時間。
即用動态規劃能解決的問題分治政策肯定能解決,隻是運作時間長了。是以,分治政策一般用來解決子問題互相對立的問題,稱為标準分治,而動态規劃用來解決子問題重疊的問題。
将「動态規劃」的概念關鍵點抽離出來描述就是這樣的:
- 1.動态規劃法試圖隻解決每個子問題一次
- 2.一旦某個給定子問題的解已經算出,則将其記憶化存儲,以便下次需要同一個子問題解之時直接查表。
為什麼你學不過動态規劃?告别動态規劃,談談我的經驗
動态規劃的三大步驟:
動态規劃,無非就是利用曆史記錄,來避免我們的重複計算。而這些曆史記錄,我們得需要一些變量來儲存,一般是用一維數組或者二維數組來儲存。下面我們先來講下做動态規劃題很重要的三個步驟:
第一步:定義數組元素的含義,上面說了,我們會用一個數組,來儲存曆史數組,假設用一維數組 dp[] 吧。這個時候有一個非常非常重要的點,就是規定你這個數組元素的含義,例如你的 dp[i] 是代表什麼意思?
第二步: 找出數組元素之間的關系式,我覺得動态規劃,還是有一點類似于我們高中學習時的歸納法的,當我們要計算 dp[n] 時,是可以利用 dp[n-1],dp[n-2]…dp[1],來推出 dp[n] 的,也就是可以利用曆史資料來推出新的元素值,是以我們要找出數組元素之間的關系式,例如 dp[n] = dp[n-1] + dp[n-2],這個就是他們的關系式了。而這一步,也是最難的一步,後面我會講幾種類型的題來說。
第三步: 找出初始值。學過數學歸納法的都知道,雖然我們知道了數組元素之間的關系式,例如 dp[n] = dp[n-1] + dp[n-2],我們可以通過 dp[n-1] 和 dp[n-2] 來計算 dp[n],但是,我們得知道初始值啊,例如一直推下去的話,會由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了,是以我們必須要能夠直接獲得 dp[2] 和 dp[1] 的值,而這就是所謂的初始值。
有了初始值,并且有了數組元素之間的關系式,那麼我們就可以得到 dp[n] 的值了,而 dp[n] 的含義是由你來定義的,你想求什麼,就定義它是什麼,這樣,這道題也就解出來了。
參考文章:
為什麼你學不會遞歸?告别遞歸,談談我的一些經驗
再談循環&疊代&回溯&遞歸&遞推這些基本概念
遞歸與疊代的差別
尾遞歸
尾調用優化
為什麼你學不過動态規劃?告别動态規劃,談談我的經驗
作業一:
數字三角形算法:
#include<iostream>
int a[1001][1001];
using namespace std;
int main()
{
int n,i,j;
//int a[1001][1001]; //得出一個結論:當數組在主函數内部時不宜開太大,否則導緻程式崩潰(這裡a[1001][1001]太大,a[101][101]OK)
cin>>n;
for (i=1; i<=n; i++)
for (j=1; j<=i; j++)
cin>>a[i][j];
for (i=n-1; i>=1; i--){
for (j=1; j<=i; j++)
{
if (a[i+1][j]>=a[i+1][j+1])
a[i][j]+=a[i+1][j];
else
a[i][j]+=a[i+1][j+1];
}
}
cout<<a[1][1]<<endl;
return 0;
}
小朋友上台階(斐波那契數列):
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
int f1=1,f2=2,f;
int n;
cin>>n;
for (int i=3; i<=n; ++i)
{
f=f1+f2;
f1=f2;
f2=f;
}
if(n==1) cout<<1<<endl;
else if(n==2) cout<<2<<endl;
else cout<<f<<endl;
return 0;
}
輸油管道問題:
#include<stdio.h>
#include<stdlib.h> //abs函數對浮點數操作會報錯
#include<math.h>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
int a[1000]; //記錄y坐标
int select(int left, int right, int k)
{
//找到了第k小的元素:
if (left >= right) return a[left];
int i = left;
int j = right+1;
int pivot = a[left];
while (true)
{
do {
i = i+1; //從第i+1位置向右掃描,找出a[i]>pivot的值停止
} while (a[i] < pivot);
do {
j = j-1; //從第j-1位置向左掃描(實際第一次是原來位置的right(right+1-1),直到a[j]<pivot停止
} while (a[j] > pivot);
if (i >= j) break; //表示沒有可交換的對象了
swap(a[i], a[j]); //交換完畢後指針i繼續從i+1位置繼續向右掃描,指針j繼續從j+1位置向左掃描
}
if (j-left+1 == k) return pivot;
//此時的a[j]比a[left](pivot)小,是以互相交換一下,此時a[j]左邊比a[j]小,右邊比a[j]大,完成一次排序劃分
//對于a[j]左邊的資料進行二次劃分則以第一次的a[j]為pivot(a[left])
//這樣數組的資料沒有丢失且完成了對pivot的一次劃分
a[left] = a[j];
a[j] = pivot;
if (j-left+1 < k)
return select(j+1, right, k-j+left-1);
else return select(left, j-1, k);
}
int main()
{
int n; //油井的數量
int x; //x坐标,讀取後丢棄
cin>>n;
for(int k=0; k<n; k++)
cin>>x>>a[k];
sort(a,a+n); //按升序排序
//計算各油井到主管道之間的輸油管道最小長度總和
int min=0;
for(int i=0; i<n; i++)
min += (int)fabs(a[i]-a[n/2]); //abs函數與fabs函數差別
cout<<"采用對數組a排序,取中間的元素的算法求解: "<<min<<endl;
//abs函數與fabs函數差別:
//C語言中:
//abs函數包含在<stdlib.h>頭檔案中,隻對整型求絕對值,對浮點數求整會報錯
//fabs函數包含在<math.h>頭檔案中,對浮點數求絕對值,對整數求絕對值會出現問題
//是以在C語言中一定要選對函數
/*
// 使用fabs求一個整數的絕對值
printf("fabs(-3)(%%d): %d\n", fabs(-3));
printf("fabs(-3)(%%f): %f\n\n", fabs(-3));
// 使用abs求一個浮點數的絕對值
printf("abs(-3.14)(%%d): %d\n", abs(-3.14));
printf("abs(-3.14)(%%f): %f\n", abs(-3.14));
*/
//C++中二者沒有差別,都包含在<cmath>頭檔案中,都可以對浮點數進行操作
/*
double a=10;
double b=-90;
cout<<abs(a)<<" "<<fabs(b)<<endl;
*/
// int n; //油井的數量
// int x; //x坐标,讀取後丢棄
cin>>n;
for (int i=0; i<n; i++)
cin>>x>>a[i];
int y = select(0, n-1, n/2); //采用分治算法計算中位數(選擇數組中第n/2小的數,即中位數)
//計算各油井到主管道之間的輸油管道最小長度總和
min=0;
for(int i=0; i<n; i++)
min += (int)fabs(a[i]-y);
cout<<"采用分治政策求中位數的算法求解: "<<min<<endl;
/*
快速排序算法是分治政策的典型應用,不過不是對問題進行等份分解(二分法),
而是通過分界資料(支點)将問題分解成獨立的子問題。
記一趟快速排序後,分解出左子集中元素個數為 nleft,則選擇問題可能是以下幾種情況之一:
nleft =k﹣1,則分界資料就是選擇問題的答案。
nleft >k﹣1,則選擇問題的答案繼續在左子集中找,問題規模變小了。
nleft <k﹣1,則選擇問題的答案繼續在右子集中找,問題變為選擇第k-nleft-1 小的數,問題的規模變小了。
此算法在最壞情況時間複雜度為 O(n2) ,此時nleft總是為0,左子集為空,即第k小元素總是位于right子集中。
平均時間複雜度為 O(n )。
*/
/*
result:
5
1 2
2 2
1 3
3 -2
3 3
采用對數組a排序,取中間的元素的算法求解: 6
5
1 2
2 2
1 3
3 -2
3 3
采用分治政策求中位數的算法求解: 6
*/
}
最大子段和問題:
#include<iostream>
using namespace std;
#define NUM 1001
int a[NUM];
int MaxSum(int n, int &besti, int &bestj)
{
int sum=0;
int b=0;
int begin=0;
for(int i=1;i<=n;i++)
{
if(b>0)
b+=a[i];
else{
b=a[i];
begin = i;
}
if (b>sum) //得到新的最優值時,更新最優解
{
sum = b;
besti = begin;
bestj = i;
}
}
return sum;
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int besti=0;
int bestj=0;
int sum=MaxSum(n,besti,bestj);
cout<<sum<<" "<<"首位址:"<<besti<<" 尾位址:"<<bestj<<endl;
return 0;
}
0-1背包動态規劃:
#include <iostream>
using namespace std;
int w[105], val[105]; //用w[]和val[]數組分别表示每件物品的重量和價值
int dp[105][1005]; //利用dp[][]來記錄輸入m項物品和t容量時的最大價值
int main()
{
int m, t;
cin >> m >> t;
for(int i=1; i<=m; i++)
cin >> w[i] >> val[i];
/*
//初始化或者置零等操作(這裡無需初始化,數組預設值為零)
for(int i=1; i<=m; i++) //物品
{
for(int j=t; j>=0; j--) //容量
{
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
*/
for(int i=1; i<=m; i++) //物品
for(int j=t; j>=0; j--) //容量
{
if(j >= w[i]) //容量大于物品品質的時候,表示物品可以裝,這時候選擇裝或者不裝兩個狀态
dp[i][j] = max(dp[i-1][j-w[i]]+val[i], dp[i-1][j]);
else //容量小于物品品質的時候,裝不下
dp[i][j] = dp[i-1][j];
}
cout << dp[m][t] << endl;
/*
//test_cout
for(int i=1; i<=m; i++) //物品
{
for(int j=t; j>=0; j--) //容量
{
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
*/
return 0;
}
//優化(将二維數組轉換成一維數組實作空間優化):
//f[j]=max(f[j-w[i]]+v[i],f[j]);
/*
//求解将哪些物品裝入背包可使這些物品的重量總和不超過背包承重量t,且價值總和最大。
#include <stdio.h>
#include <string.h>
int f[1010],w[1010],v[1010];//f記錄不同承重量背包的總價值,w記錄不同物品的重量,v記錄不同物品的價值
int max(int x,int y){//傳回x,y的最大值
if(x>y) return x;
return y;
}
int main(){
int t,m,i,j;
memset(f,0,sizeof(f)); //總價值初始化為0
scanf("%d %d",&t,&m); //輸入背包承重量t、物品的數目m
for(i=1;i<=m;i++)
scanf("%d %d",&w[i],&v[i]); //輸入m組物品的重量w[i]和價值v[i]
for(i=1;i<=m;i++){ //嘗試放置每一個物品
for(j=t;j>=w[i];j--){//倒叙是為了保證每個物品都使用一次
f[j]=max(f[j-w[i]]+v[i],f[j]);
//在放入第i個物品前後,檢驗不同j承重量背包的總價值,如果放入第i個物品後比放入前的價值提高了,則修改j承重量背包的價值,否則不變
}
}
printf("%d\n",f[t]); //輸出承重量為t的背包的總價值
return 0;
}
*/
/*
輸入:
4 5
1 2
2 4
3 4
4 5
輸出:
8
*/
背包問題的貪心算法:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
struct Pair{ //每個物品的機關價值(機關價值如果沒說的話,可以采用總價值除以總品質擷取機關價值)和總重量
int cost;
int weight;
};
bool cmp( const Pair &x,const Pair &y) //預設排序方式是按機關品質的價值高低進行排序,價值高者優先放(貪心政策)
{
return x.cost > y.cost;
}
int n, s, m, v, w; //s件物品,v和m表示輸入的價值和品質,n表示執行n次
const int maxn=100001;
Pair pack[maxn];
int sum=0;
int main()
{
cin>>n; //表示執行次數
while(n--)
{
scanf("%d%d",&s,&m);
sum=0;
for(int i=1;i<=s;i++)
{
pack[i].cost=0;
pack[i].weight=0;
}
for(int i=1;i<=s;i++)
{
scanf("%d%d",&v,&w);
pack[i].cost=v;
pack[i].weight=w;
}
sort( pack+1,pack+s+1,cmp);
//開時裝包
int i;
for(i=1;i<=s;i++) //從第一件物品(價值高者)開始裝,這樣按照價值高者的優先政策依次裝入背包
{
//如果某一件物品的總量超過了該背包的剩餘總量,
//也就是可以按照将該物品瓜分的政策進行裝取:
//sum+=pack[i].cost*m;方式進行,然後跳出循環(背包已滿)
if(pack[i].weight > m)
{
sum+=pack[i].cost*m;
break;
}
else //全裝下背包也不滿,那就全裝下,然後總價值增加,容量減少
{
sum+=pack[i].cost*pack[i].weight;
m-=pack[i].weight;
}
}
printf("%d\n",sum);
}
return 0;
}
/*
//test:
//輸入:
1
3 15
5 10
2 8
3 9
//輸出:
65
*/
木棒的加工:
//每一次加工,開頭第一個長度序列的先加工完,之後,再在長度不同的序列,
//找出重量比最後加工的木棒重量還要大的木棒,進行加工,直至找不到為止。
//(這就變成了長度比較确定後尋找品質最長單調遞增子序列的個數。)
#include<bits/stdc++.h>
using namespace std;
#define maxN 5001
struct stick
{
int l; //木棒的長度
int w; //木棒的重量
}data[maxN]; //所存放的木棒
int cmp(stick a,stick b)
{
if(a.l==b.l)return a.w<b.w; //長度相同時,按重量排序
else if(a.l<b.l)return true; //優先按長度排序
return false;
}
int LIS(int n,stick a[])//木棒數量 木棒參數的數組
{
int b[maxN];//木棒分組的序号
memset(b,0,sizeof(b));//給b賦初值為0,長度為maxN
int i,j,k;
b[0]=1; //邊界條件
for(i=1;i<n;i++)
{//計算第i個木棒的分組序号
k=0;
for(j=0;j<i;j++)
if(a[i].w<a[j].w&&k<b[j])k=b[j]; //關系式
b[i]=k+1;
}
//查找最大的分組序号(數組b中的最大值)
int max=0;
for(i=0;i<n;i++)
if(b[i]>max)max=b[i];
return max;
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>data[i].l>>data[i].w;//4 9 5 2 2 1 3 5 1 4
}
sort(data,data+n,cmp);
int bb=LIS(n,data);
cout<<bb;
}
魚塘釣魚問題:
#include <cstdio>
using namespace std;
int t[101],f[101],d[101],f1[101],la,n,m,max;
int main(){
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&f[i]);
for (int i=1;i<=n;i++) scanf("%d",&d[i]);
for (int i=1;i<n;i++) scanf("%d",&t[i]);
scanf("%d",&m);
for (int k=1;k<=n;k++){
int ti=m-la,ans=0,j=0;
for (int i=1;i<=k;i++) f1[i]=f[i];
for (int i=1;i<=k;i++) if (f1[i]>f1[j]) j=i;//找最大值
while (ti>0&&f1[j]>0){
if (f1[j]>0) ans+=f1[j];
f1[j]-=d[j];
for (int i=1;i<=k;i++) if (f1[i]>f1[j]) j=i;//更新
ti--;
}
max=(max>ans)?max:ans;
la+=t[k];
}
printf("%d",max);
return 0;
}
/*
test:
輸入:
5
10 14 20 16 9
2 4 6 5 3
3 5 4 4
14
輸出:
76
*/
實驗一:
楊輝三角形:
#include <stdio.h>
int main()
{
int i, j, n, a[34][34];
scanf("%d", &n);
for (i = 0; i < n; i++)
{
a[i][0] = 1;
a[i][i] = 1;
for (j = 1; j < i; j++)
a[i][j] = a[i-1][j-1] + a[i-1][j];
}
for (i = 0; i < n; i++)
{
for (j = 0; j <= i; j++)
printf("%d ", a[i][j]);
printf("\n");
}
return 0;
}
字元串對比:
#include<stdio.h>
#include<string.h>
int main()
{
int len1,len2;
char ch1[10],ch2[10];//定義字元串數組
scanf("%s%s",ch1,ch2);
len1=strlen(ch1);//求字元串長度
len2=strlen(ch2);
if(len1==len2)//判斷字元串長度是否相等
{
int flag=1;//定義一個辨別符
for(int i=0;i<len1;i++)
if(ch1[i]!=ch2[i])//判斷如果不相同
flag=0;//使辨別符變化
if(flag) printf("2");//判斷,如果辨別符沒有改變,則符合條件2
else
{
flag=1;//重新定義辨別符
for(int i=0;i<len1;i++)//判斷,如果在忽略大小寫的情況下是否還是不同
if(ch1[i]+32!=ch2[i]&&ch1[i]-32!=ch2[i]&&ch1[i]!=ch2[i])
flag=0;//使辨別符改變
if(flag) printf("3");//如果辨別符沒有改變 ,則符合條件3
else printf("4");//否則符合條件4
}
}
else printf("1");//否則符合條件1
}
攔截飛彈(LIS,貪心,動态規劃):
//LIS解法,将飛彈攔截問題轉化為最長上升子序列問題(最長不遞增子序列)
#include<stdio.h>
#include<string.h>
int Height[101]; //發射過來的飛彈高度
int MaxLen[101]; //發射第i顆飛彈處記錄的最大不上升子序列的個數
int Maxint[101]; //用來記錄發射第i顆飛彈需要的最大攔截飛彈系統的個數
void LIS(int k){ //攔截飛彈問題即找出最長不上升子序列問題
memset(MaxLen,0,sizeof(MaxLen));
memset(Maxint,0,sizeof(Maxint));
for(int i = 1;i <= k; i++){
MaxLen[i] = 1;
Maxint[i]=1;
//周遊其前所有飛彈高度
for(int j = 1;j < i;j++){
//如果目前飛彈高度小于等于j号飛彈
if(Height[i] <= Height[j]){
//把目前飛彈放在j号飛彈後,其最長不增子序列長度為j号飛彈結尾的最長不增子序列長度 + 1
int preMax = MaxLen[j] + 1;
if(preMax > MaxLen[i]){
MaxLen[i] = preMax;
}
}
else{ //如果目前飛彈高度大于j号飛彈高度,那麼我們就需要增加飛彈系統攔截
int preMaxint = Maxint[j] + 1;
if(preMaxint > Maxint[i]){
Maxint[i] = preMaxint;
}
}
}
}
}
int main()
{
int N,i; //N表示發射過來的飛彈數量
while(scanf("%d",&N)!=EOF){
//輸入飛彈高度
for(i = 1;i <= N;i++){
scanf("%d",&Height[i]);
}
LIS(N);
int Max = -1;
int ans = -1;
//輸出最長不增子序列的長度即能攔截的飛彈數
for(i = 1;i <= N;i++){
if(Max < MaxLen[i]){
Max = MaxLen[i];
}
if(ans < Maxint[i]){
ans = Maxint[i];
}
}
if(N != 0){
printf("%d %d\n",Max,ans);
}
}
return 0;
}
/*
//用于解此題的還有動态規劃和貪心算法求解:
//動态規劃求解:
for(int i=1; i<=n; i++)
{
for(int j=0; j<i; j++) //與前面每一個比較一次
{
if(a[j]<a[i]) //需要多加1個系統 (a[]數組用于存放飛彈高度)
dp[i]=max(dp[i],dp[j]+1); //選出需要最少系統的最大值 (dp[]初始值為1)
//将待求解問題分解成若幹個子問題,先求解子問題,然後從這些子問題的解得到原問題的解。(展現了動态規劃的思想)
}
}
sort(dp,dp+n);
cout<<dp[n-1]<<endl;
//貪心算法求解:
while(~scanf("%d",&n)) //n表示飛彈個數
{
int x,sum=0;
dp[maxn]={0};
for(int i=0;i<n;i++)
{
cin>>x;int j; //x表示飛彈高度
//利用sum表示目前至少有多少系統,并在每次飛彈發射時周遊這些系統所能攔截的最大高度,
//進行比較後如果能攔截,即x<=dp[j]則更新該系統的最大攔截高度值,否則則周遊下一個最大攔截高度值,
//如果都沒有,那麼就是周遊到了最後,此時j=sum+1>sum,則增加一個新系統去攔截該飛彈
//這裡每次都拿已有的最大高度值去和新發射的飛彈高度值進行比較,
//即從問題的初始狀态出發,直接去求每一步的最優解,
//通過若幹次的貪心選擇,最終得出整個問題的最優解(展現了貪心算法的思想)
for(j=1;j<=sum;j++)
{
if(x<=dp[j]) //這裡的dp[j]表示該系統在j處能攔截的最大高度
{
dp[j]=x; //更新該系統下一個能攔截的最大高度
break;
}
}
if(j>sum) //前面的系統不能攔截
{
dp[++sum]=x;//新加一個系統并且指派下一次能攔截的高度
}
}
cout<<sum<<endl;
}
*/
/*
//test:
//輸入:
8
389 207 155 300 299 170 158 65
//輸出:
6 2
*/
八(n)(2n)皇後問題:
#include<iostream>
#include <cstdio>
using namespace std;
int arry[10][10];
int count=0; //存儲方案結果數量
bool check(int k,int j){ //判斷節點是否合适(k代表行,j代表列)
for(int i=0;i<8;i++){ //檢查行列沖突(其實這裡隻檢查列沖突即可,行是周遊來的,是不會産生沖突的)
if(arry[i][j]==1){
return false;
}
}
for(int i=k-1,m=j-1; i>=0 && m>=0; i--,m--){ //檢查左對角線
if(arry[i][m]==1){
return false;
}
}
for(int i=k-1,m=j+1; i>=0 && m<=7; i--,m++){ //檢查右對角線
if(arry[i][m]==1){
return false;
}
}
return true;
}
void print(){ //列印結果
cout<<"方案"<<count<<":"<<endl;
for(int i=0;i<8;i++){
for(int m=0;m<8;m++){
if(arry[i][m]==1){
cout<<"o ";
}
else{
cout<<"+ ";
}
}
cout<<endl;
}
cout<<endl;
}
void findQueen(int i){//尋找皇後節點
if(i>7){//八皇後的解
count++;
print();//列印八皇後的解
return;
}
for(int m=0;m<8;m++){ //深度回溯,遞歸算法
if(check(i,m)){ //檢查皇後擺放是否合适
arry[i][m]=1;
findQueen(i+1); //合适則置一,并往下遞歸調用求解
arry[i][m]=0; //清零,以免回溯的時候出現髒資料(這一步是找到結果之後進行的操作,防止影響下一個結果,恢複到上一步的初始狀态)
}
}
}
int main() {
findQueen(0); //從第0行開始,如果是i,則表示前i行沒有擺放的皇後,不會影響後面的排列,變成8-i個皇後在沒有限制的8-i行尋找位置
cout<<"八皇後問題共有:"<<count<<"種可能"<<endl;
}
實驗二:
Fibonacci數列:
#include <stdio.h>
int F(int n)
{
int i, s1 = 1, s2 = 1, s3 = 1;
for (i = 3; i <= n; i++)
{
s3 = s1 + s2;
if (s3 > 10007)
s3 -= 10007;
s1 = s2;
s2 = s3;
}
return s3;
}
int main()
{
int n;
scanf("%d", &n);
printf("%d", F(n));
return 0;
}
校門外的樹:
#include <iostream>
using namespace std;
int main()
{
int L,M;
int num[10001]={0};
int n=0;
cin>>L>>M;
int a[100],b[100];
for(int i=0;i<M;i++)
{
cin>>a[i]>>b[i];
for(int j=a[i];j<=b[i];j++)
{
num[j]=1;
}
}
for(int i=0;i<=L;i++)
{
if(num[i]==0)
{
n++;
}
}
cout<<n;
return 0;
}
奪寶奇兵:
#include <iostream>
#include<algorithm>
using namespace std;
int arr[101][101], dp[101][101];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j <= i; j++)
cin >> arr[i][j];
for (int i = n - 1; i >= 0; i--)
for (int j = 0; j <= i; j++)
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + arr[i][j]; //動态規劃,狀态轉移方程
//dp[0][0]位置縮小正好是[0][0]位置,從底部回溯到頂部結果
cout << dp[0][0];
/*
從頂部推到底部(結果在底部位置,但是不能确定,要通過比較篩選确定)
int maxnum=0;
for(i=1;i<=n;i++){
for(j=1;j<=i;j++){
dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+mountain[i-1][j-1];
if(maxnum<dp[i][j])
maxnum=dp[i][j];
}
}
cout <<maxnum<<endl;
*/
return 0;
}
/*
test:
輸入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
輸出:
30
*/
分解質因數:
#include<stdio.h>
int main()
{
int a,b,i,d,c,j;
scanf("%d%d",&a,&b);
if(a<=b&&a>=2&&a<=10000&&b<=10000)
{
for(i=a;i<=b;i++)
{
d=1;
for(j=2;j<i;j++)
if(i%j==0)
{
d=0;
break;
}
if(d==1)
printf("%d=%d\n",i,i);
else if(d==0)
{
printf("%d=",i);
j=2;
c=i;
while(1)
{
while(c%j==0)
{
printf("%d",j);
c=c/j;
if(c!=1)
printf("*");
}
if(c==1)
{
printf("\n");
break;
}
j++;
}
}
}
}
return 0;
}
寫在最後:
算法的學習有兩個困難的地方(參考文章:算法之美(豆瓣讀書)):
其一,我們學習了那些經典的算法,除了贊歎一下設計的巧思,但總難免問上一句:怎麼想到的?對學生來說,這可能是最費解、也最讓人窩火的地方。我們下再多的功夫去記憶書上的算法、去分析這些算法的效率,卻終究不能理喻得到這些算法的過程。心理盤算着:給我一個新問題,讓我設計個算法出來,我能行嗎?答案是:不知道。
可這偏偏又是極重要的,無論作研究還是實際工作,一個計算機專業人士最重要的能力,就是解決問題——解決那些不斷從理論模型、或者從實際應用中冒出來的新問題。
其二,算法作為一門學問,有兩條正交的線索。一個是算法處理的對象:數、矩陣、集合、串(strings)、排列(permutations)、圖(graphs)、表達式(formula)、分布(distributions),等等。另一個是算法的設計思想:貪婪、分治、動态規劃、線性規劃、局部搜尋(local search),等等。這兩條線索幾乎是互相獨立的:同一個離散對象,例如圖,稍有不同的問題,例如single-source shortest path和all-pair shortest path,就可以用到不同的設計思想,如貪婪和動态規劃;而完全不同的離散對象上的問題,例如排序和整數乘法,也許就會用到相同的思想,例如分治。
兩條線索交織在一起,該如何表述。對學生而言,不同離散對象的差别是直覺的——我們已經慣于在一章裡面完全講排序、而在另一章裡面完全講圖論算法;可是對算法而言,設計思想的差别是根本的,因為這是從問題的結構來的:不同離散對象上面定義的問題,可以展現出類似的結構,而這結構特征,就是支援一類算法的根本,也是我們設計算法的依據。
很多時候我們會為算法的複雜難想或者滿滿套路而煩惱,但是在思考過後又會覺得還蠻有意思,學到了很多,很有成就感,或許這就是算法的魅力吧。