二叉樹

一、樹
- 1、定義與特點
- 2、相關術語
- 3、性質
- 4、樹節點與度之間的關系
二、二叉樹
- 1、定義
- 2、與度為 2 的有序樹的差別
- 3、特殊二叉樹
- - 3.1、滿二叉樹
  - 3.2、完全二叉樹
  - 3.3、二叉排序樹
  - 3.4、平衡二叉樹
- 4、性質
- 5、存儲結構
- 6、基本操作
三、二叉樹實作
四、二叉樹的周遊
- 1、先序周遊
- 2、中序周遊
- 3、後序周遊
- 4、三序周遊的非遞歸算法
- 5、層次周遊
- 6、周遊序列的應用
- - 6.1、确定二叉樹
  - 6.3、其他應用

一、樹

1、定義與特點

樹， 是 n 個節點的有限集，或為空樹（n=0），或為非空樹 。
對于任何一棵非空樹：

1）有且僅有一個稱之為
根
的節點；

2）除根節點外，其餘節點可分為 m 個互不相交的有限集 T1，T2……Tm，其中每個集合本身又是一棵樹，稱為
根的子樹 。
樹的定義是遞歸的，樹的資料結構也是遞歸的。作為一種邏輯結構和分層結構，具有如下特點：

1）
根節點無前驅
，根節點外的節點有且隻有一個前驅；

2）樹中所有結點可以有
零個或多個後繼 。

2、相關術語

1）祖先與子孫：對于樹中的任何一個節點B，從根節點 通往該節點B的路徑上的所有經過節點都是其祖先 ，反過來， B 是該路徑上任意節點的子孫 。
2）雙親與孩子：樹中某結點B，與其 直接相連的前驅節點 為B的 雙親節點 ，而B的 直接後繼為其孩子節點 。
3）兄弟節點：具有 相同雙親節點 的節點稱為兄弟節點。
4）節點度與樹的度：節點度，指 節點的孩子數 ；而所有結點的節點度中最大值稱為樹的度。
5）分支節點與葉子節點： 度大于 0 的節點稱為分支節點，也稱非終端節點； 度為 0 的節點稱為葉子節點，也叫終端節點。
6）節點的深度、高度和層次：節點的層次是從 根 開始定義的，根節點為第一層，由根節點往葉子節點依次增加，同一層節點非相同雙親的節點可稱為堂兄弟。節點深度是 從根節點開始自頂向下逐層累加 ，節點的高度是 從葉子節點開始自底向上逐層累加的 。樹的高度或深度就是樹中結點的最大層數。
7）有序樹和無序樹： 樹中結點的各子樹從左到右是有次序的，不能互換的 ，稱該樹是有序的，否則就是無序樹。
8）路徑和路徑長度：樹中兩個節點之間的路徑， 由這兩個節點之間所經過的節點序列 構成，路徑長度 是指路徑上所經過的邊的個數。
9）森林： m 棵互補相交的樹的集合 。

3、性質

樹具有如下性質：

1）樹中的
節點數 等于 所有節點的度數加1
2）度為 m 的樹中第 i 層上至多有 m(i-1) 個節點（i>=1）

3）高度為 h 的 m 叉樹至多有(mh-1)/(m-1)個節點。

4）具有 n 個節點的 m 叉樹的最小高度為 logm(n(m-1)+1) 向上取整

4、樹節點與度之間的關系

1）總節點數 = n0+n1+n2+……+nm，ni 表示度為 i 的節點的個數

2）總分支數 = 1n1+2n2+……+mnm，度為 m 的節點引出 m 條分支

3）總結點數 = 總分支數 + 1。

二、二叉樹

1、定義

Binary Tree 是 n 個節點所構成的集合，或為空樹，或為非空樹。
任意非空樹：

1）有且僅有一個根節點。

2）根節點以外的節點分為兩個互不相交的子集 T1和T2，分别稱為左子樹和右子樹，且左子樹和右子樹本身也是二叉樹。
二叉樹 是有序樹，不可随便調換左右子樹的順序 。

2、與度為 2 的有序樹的差別

差別有兩個：

1）度為 2 的樹，
至少有 3個節點
，而二叉樹可以為空；

2）度為 2 的有序樹的孩子的左右次序是相對另一個孩子而言的，若某結點隻有一個孩子，則這個孩子無需分左右次序；而二叉樹無論孩子數是1還是2，均需确定左右次序，即二叉樹的節點順序不是相對另一個節點而言的，而是确定的。

3、特殊二叉樹

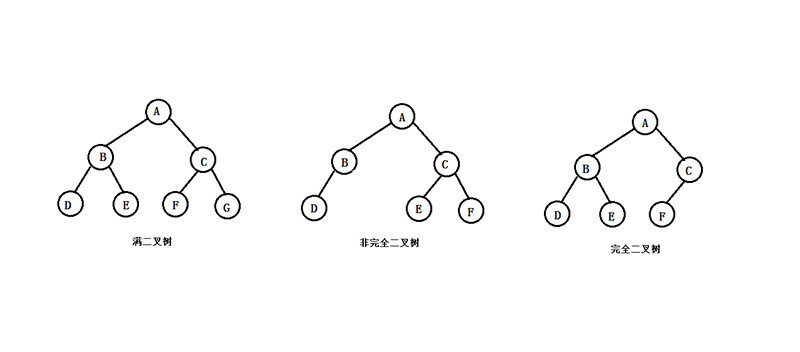
3.1、滿二叉樹

指 高度為 h 的二叉樹，含有 2^h - 1 個節點 ，也即每層都含有最多的節點。
對于滿二叉樹，若從根節點到葉子，從左向右，依次編号，即根節點為 1，根節點的左孩子為 2，根節點右孩子為 3，以此類推……則編号為 i 的節點， 其雙親為 i/2 向下取整 ， 左孩子為 2i ， 右孩子為 2i+1 .

3.2、完全二叉樹

指 樹高為 h，節點數為 n 的二叉樹，當且僅當每個結點都與高度為 h 的滿二叉樹中編号為 1~n 的節點一一對應的二叉樹 。

資料結構學習筆記之C++實作二叉樹一、樹二、二叉樹三、二叉樹實作四、二叉樹的周遊
滿二叉樹有如下特點：

1）若
i<=|n/2| ，則 節點 i 為分支節點，否則為葉子節點
。

2）
葉子節點 隻可能在 層次最大的兩層上 出現。對于 最大層次中的葉子節點 ，都依次排列在該層 最左邊的位置
上。

3）
度為 1 的節點隻可能有一個，且該節點隻有左孩子
。

4）按層次編号，編号為
i 的節點為葉子節點或隻有左孩子 ，則編号 大于 i 的節點均為葉子節點
。

5）
n 為奇數 ，則每個 分支節點都有左孩子和有孩子 ； n 為偶數 ，則編号最大的分支節點—— 編号為 n/2 的節點隻有左孩子 、沒有有孩子， 其餘節點都有左右孩子 。

3.3、二叉排序樹

左子樹上所有結點的關鍵字均小于根節點的關鍵字，右子樹上的所有結點的關鍵字均大于根節點的關鍵字 ，左子樹和右子樹各是一棵二叉排序樹。

3.4、平衡二叉樹

樹上任意一結點的左子樹和右子樹的深度之差不超過 1 。

4、性質

二叉樹有如下獨特的性質：
1）非空二叉樹的葉子節點樹等于度為 2 的節點數加一，即 n0=n1+1。
2）非空二叉樹在第 k 層上至多有 2k-1個結點（k>=1)
3）高度為 h 的二叉樹至多有 2h-1個節點（h>=1)
4）完全二叉樹，從上到下、從左到右順序編号1,2,3……n，則有以下關系：
- ① 當 i>1 時，節點 i 的雙親編号為⌊i/2⌋，即 i%2==0 時，其雙親編号為 i/2，反之則其雙親編号為（i-1)/2。
- ② 當 2i<= n 時，節點為 i 的左孩子編号為 2i，否則無左孩子。
- ③ 當 2i+1<=n 時，節點 i 的右孩子為 2i+1，否則無右孩子。
- ④ 節點 i 所在的層次為 ⌊log2n⌋+1
5）具有 n 個節點的完全二叉樹的高度為 ⌈log2(n+1)⌉ 或 ⌊log2n⌋+1。

5、存儲結構

二叉樹的實作同樣有兩種存儲結構：順序存儲和鍊式存儲。
二叉樹的順序存儲是指用一組連續的存儲單元依次自上而下、自左向右存儲節點元素 ，即節點編号為 i 的元素存儲在數組下标為 i-1 的存儲單元中。順序存儲适用于完全二叉樹和滿二叉樹，一般二叉樹的話，為了能讓數組下标反映二叉樹中節點之間的邏輯關系，需要添加一些并不存在的空節點，是以最壞情況下：高為 h，節點數為 h 的單支樹需要占據近 2h-1 個存儲單元。值得注意的是， 應當從下标為 1 的地方開始存儲二叉樹的元素。
二叉樹一般采用鍊式存儲，即用連結清單節點來存儲二叉樹中的每個節點。

6、基本操作

二叉樹的基本操作如下：

1）Create()：建立一個根節點為預設值的二叉樹。

2）Init(array)：用數組初始化一個二叉樹。

3）IsEmpty()：判空操作。

4）Depth()：傳回二叉樹的深度。

5）Root()：傳回二叉樹的根節點。

6）Value(e)：傳回e節點值。

7）Assign(&e,value)：将 value 指派給節點 i。

8）Parent(e)：若e是非根節點，傳回 e 節點的父結點。

9）LeftChild(e)：傳回 e 的左子樹。

10）RightChild(e)：傳回 e 的右子樹。

11）LeftSibling(e)：傳回 e 的左兄弟，否則傳回空。

12）RightSibling(e)：傳回 e 的右兄弟。

13）InsertChild(p,LR,C)：根據 LR 為 0或1，在 p 所指節點處插入 c，使 c 成為 p 所指節點的左或右子樹，p 所指節點的原有左或右子樹則成為 c 的右子樹。

14）DeleteChild(p,LR)：删除 p 所指的節點的左右子樹。

15）PreOrderTraverse()：先序周遊，對每個結點通路一次。

16）PostOrderTraverse()：後序周遊，對每個結點通路一次。

17）LevelOrderTraverse()：層次周遊，對每個結點通路一次。

18）Clear()：将二叉樹清空，留下根節點，并将根節點置為 0.

19）Destroy()：銷毀二叉樹。

三、二叉樹實作

二叉樹實作代碼如下：

#pragma once
#include<iostream>
using namespace std;

// 樹結點
typedef struct BitNode
{
	int data;
	BitNode* lchild, * rchild;
	BitNode* parent;
}*BTree;

// 輔助構造二叉樹的連結清單節點
typedef struct StackNode
{
	BitNode* nodePtr;
	// 用于判斷建立右子樹還是左子樹
	char flag;
	StackNode* next; //連結清單下一節點
	StackNode* pre; //連結清單前一節點
}*StackPtr;
//==============鍊棧相關操作
//鍊棧
typedef struct LStack
{
	BTree elem; //資料域
	LStack* next; //指針域
}*LinkStack;
//鍊棧初始化
void InitLS(LinkStack& ls)
{
	ls = new LStack;
	ls->next = NULL;
}
//壓棧
void push(LinkStack& ls, BTree e)
{
	LinkStack p = new LStack; //申請新節點
	p->elem = new BitNode;
	p->elem = e; //将将要壓棧的資料放入新節點資料域
	p->next = ls; //将新節點壓入棧中
	ls = p; //将棧的頭指針移到新節點，以達到更新棧的操作
}
//彈棧
void pop(LinkStack& ls, BTree& e)
{
	if (ls == NULL)
	{
		cout << "空棧，錯誤，無法彈棧！" << endl;
		exit(0);
	}
	else
	{
		e = ls->elem; //将棧頂元素彈出
		LinkStack t = new LStack; //臨時節點存放棧頂元素的位址以待後續步奏釋放該節點
		t = ls;
		ls = ls->next; //更新棧，棧表元素向棧頂方向前移一個機關
		delete t; //釋放原棧頂元素的記憶體空間
	}
}
//擷取棧頂元素
void gettop(LinkStack ls, BTree& e)
{
	if (ls != NULL)
	{
		e = ls->elem;
	}
}
//判斷棧是否是空棧
bool stackempty(LinkStack ls)
{
	if (ls == NULL)
		return true;
	return false;
}
//清空棧表
void free(LinkStack ls)
{
	delete ls;
}
//==========================
//連結清單頭結點
StackPtr S, Head;
//初始化連結清單
void InitStack(StackPtr& s)
{
	s = new StackNode;
	s->flag = 'L';
	s->next = NULL;
	s->pre = NULL;
}
//連結清單操作器
StackNode* r = new StackNode;
//二叉樹根節點，便于子樹建構完畢需要回到根節點的操作
BTree root;
//添加二叉樹節點，使用先序規則
void addNode(BTree& treeHead, int num)
{
	if (S == NULL)
	{
		cout << "錯誤，棧未初始化!" << endl;
		exit(0);
	}
	else
	{
		if (S->next == NULL)
		{
			r = S;//将連結清單訓示器與連結清單連結
		}
		if (treeHead == NULL)
		{
			StackNode* newS = new StackNode; //建立連結清單一個頭節點
			newS->next = NULL;
			newS->pre = r;//頭節點的前一個節點為連結清單位址
			r->next = newS; //将節點添加到連結清單中
			r = newS;
			treeHead = new BitNode; //初始化二叉樹根節點，并将二叉樹根節點的位址存在在連結清單頭結點中
			root = new BitNode;
			root = treeHead;
			treeHead->lchild = NULL;
			treeHead->rchild = NULL;
			treeHead->parent = NULL;
			r->nodePtr = new BitNode;
			r->nodePtr = treeHead;
			r->nodePtr->data = num; //往根節點資料域添加資料
			r->flag = 'L'; //訓示下一步構造左子樹
		}
		else if (treeHead != NULL)
		{
			BTree newnode = new BitNode;  //建立一個二叉樹節點
			newnode->data = num; //往二叉樹節點資料域添加資料
			newnode->lchild = NULL;
			newnode->rchild = NULL;
			if (r->flag == 'L') //判斷目前連結清單中的二叉樹節點是否需要構造左子樹
			{
				r->nodePtr->lchild = new BitNode;
				r->nodePtr->lchild = newnode; //将新節點添加到二叉樹的左子樹中
				newnode->parent = r->nodePtr; //左子樹的父節點為目前節點
				StackNode* newS = new StackNode; //建立連結清單新節點，用于存放二叉樹下一步的構造資訊
				newS->next = NULL;
				newS->pre = r;//連結清單新節點的前一個節點為連結清單操作器的所停留的目前節點
				newS->nodePtr = new BitNode;
				newS->nodePtr = r->nodePtr->lchild; //将連結清單新節點的二叉樹節點勾連到已構造好的左子樹中
				newS->flag = 'L';
				r->next = newS; //使用連結清單操作器将新的連結清單節點添加到連結清單中
				r = newS; //移動連結清單操作器的位置
			}
			else if (r->flag == 'R')//判斷目前連結清單中的二叉樹節點是否需要構造右子樹
			{
				if (r->nodePtr == root) //如果要構造的是根節點的右子樹
				{
					r->nodePtr->rchild = new BitNode;
					r->nodePtr->rchild = newnode;//将新節點添加到二叉樹的右子樹中
					r->nodePtr->rchild->parent = r->nodePtr;//右子樹的父節點為目前節點
				}
				else //構造普通右子樹
				{
					r->nodePtr->rchild = new BitNode;
					r->nodePtr->rchild = newnode;//将新節點添加到二叉樹的右子樹中
					newnode->parent = r->nodePtr;//右子樹的父節點為目前節點
				}
				StackNode* newS = new StackNode; // 建立連結清單新節點，用于存放二叉樹下一步的構造資訊
				newS->next = NULL;
				newS->pre = r;//連結清單新節點的前一個節點為連結清單操作器的所停留的目前節點
				newS->nodePtr = new BitNode;
				newS->nodePtr = r->nodePtr->rchild;//将連結清單新節點的二叉樹節點勾連到已構造好的右子樹中
				newS->flag = 'L';
				r->next = newS;//使用連結清單操作器将新的連結清單節點添加到連結清單中
				r = newS;//移動連結清單操作器的位置
			}
		}
	}
}
//判斷二叉樹節點是否為葉子節點，是傳回True，否則傳回false
bool IsLeaf(BTree t)
{
	if (t->lchild == NULL && t->rchild == NULL)
	{
		return true;
	}
	return false;
}
//處理二叉樹不需要構造左子樹或右子樹
void processEmptyData()
{
	if (r->flag == 'L') //如果是左子樹不需要構造，隻需将構造标志改為右子樹
	{
		r->flag = 'R';
	}
	else if (r->flag == 'R')//如果是右子樹不需要構造
	{
		if (r->nodePtr->parent->rchild != NULL)
		{
			if (IsLeaf(r->nodePtr->parent->lchild)) //兩個if語句形成判斷目前遊離二叉樹節點是處于左子樹的右葉子處
			{
				r->pre = S->next;//将目前連結清單節點的前一個節點更改為頭結點
				r->nodePtr = root; //将目前遊離二叉樹節點移動到二叉樹根節點處
			}
		}
		r->nodePtr = r->pre->nodePtr; //普通情況下，當右子樹不需要構造時，将連結清單操作器前移一位，
										//使遊離二叉樹節點順着以構造的二叉樹前移一個節點
	}
}
//二叉樹各個節點已構造完畢時所要進行的操作
void processEndData()
{
	StackNode* end = r;
	S = Head; //避免連結清單首元節點意外移動
	r = S; //将連結清單操作器停放會連結清單首元結點
	delete end;//釋放對于連結清單節點
}
//以先序規則構造二叉樹
void createBiTreeNonRecursive(BTree& treeHead)
{
	int num;
	bool keepRun = true;
	treeHead = NULL;
	InitStack(S);//初始化連結清單
	Head = new StackNode;
	Head = S;//标志連結清單首元節點位址
	cout << "請按照構造規則輸入二叉樹的結點資料：" << endl;
	while (keepRun)
	{
		cin >> num; //輸入即将添加到二叉樹節點中的資料
		switch (num) //判斷輸入的數值
		{
		case -1://如果是-1，則轉到不需要構造左子樹或右子樹的操作
			processEmptyData();
			continue;
		case 0://如果是0,則轉到二叉樹構造完畢的操作
			processEndData();
			keepRun = false; //終止循環
			break;
		default: //0和-1以外的其他數值，轉到構造二叉樹節點的操作
			addNode(treeHead, num);
		}
	}
}
//求葉子數
int leaf = 0;
//求葉子數
void leafCount(BTree rt)
{
	if (rt != NULL)
	{
		leafCount(rt->lchild);
		leafCount(rt->rchild);
		if (rt->lchild == NULL && rt->rchild == NULL)//如果目前二叉樹節點是葉子，則葉子數加一
			leaf++;
	}
}
//求二叉樹節點數
int node(BTree rt)
{
	if (rt == NULL)
		return 0;
	int leftcount = node(rt->lchild);
	int rightcount = node(rt->rchild);
	int ret = leftcount + rightcount + 1;
	return ret;
}
//==============先序遞歸周遊==============
void rDLR(BTree rt)
{
	if (rt)
	{
		cout << rt->data << " "; //先輸出根節點
		rDLR(rt->lchild); //再周遊左子樹
		rDLR(rt->rchild);//最後周遊右子樹
	}
}
//========================================
//===========非遞歸先序周遊
void DLR(BTree rt)
{
	LinkStack ls;
	BTree p = new BitNode;
	BTree q = new BitNode;
	p = rt;
	int count = 0;
	InitLS(ls);
	if (p == NULL)
	{
		cout << "樹空" << endl;
		return;
	}
	while (p || !stackempty(ls))
	{
		if (count == leaf)  //當目前二叉樹節點是二叉樹最後一個葉子節點時 ，無需後續操作，結束函數調用
		{
			free(ls);
			return;
		}
		if (p)
		{
			if (p != NULL)
			{
				push(ls, p); //将二叉樹的非空節點壓入棧中
			}
			cout << p->data << " "; //先輸出根節點
			p = p->lchild; //再周遊左子樹
		}
		else
		{
			pop(ls, q); //彈出棧中的非空二叉樹節點
			p = q->rchild; //最後周遊右子樹
		}
		if (IsLeaf(q)) //累計葉子數
		{
			count++;
		}
	}
}
//========中序遞歸算法
void rLDR(BTree rt)
{
	if (rt)
	{
		rLDR(rt->lchild);//先周遊左子樹
		cout << rt->data << " ";//再輸出根節點
		rLDR(rt->rchild);//最後周遊右子樹
	}
}
//中序非遞歸算法
int size2 = 0;
void LDR(BTree rt)
{
	LinkStack ls;
	BTree p = new BitNode;
	BTree q = new BitNode;
	p = rt;
	size2 = node(rt);
	int nodecount = 0;
	int count = 0;//周遊節點計數
	InitLS(ls);
	if (p == NULL)
	{
		cout << "樹空" << endl;
		return;
	}
	while (p || !stackempty(ls))
	{
		if (leaf != 1) //當二叉樹不是隻有左子樹或右子樹的情況
		{
			if (count == leaf && nodecount == size2)//當目前二叉樹節點是二叉樹最後一個葉子節點且已經周遊完所有的節點時 ，
												//無需後續操作，結束函數調用
			{
				free(ls);
				return;
			}
			if (p)
			{
				if (p != NULL)
				{
					push(ls, p);//将二叉樹的非空節點壓入棧中
				}
				p = p->lchild; //先周遊左子樹
			}
			else
			{
				pop(ls, q);//彈出棧中的非空二叉樹節點
				cout << q->data << " "; //再輸出根節點
				nodecount++;//累計已經周遊的節點數目
				if (q->rchild != NULL)
				{
					p = q->rchild; //最後周遊右子樹
				}
			}
			if (IsLeaf(q))//累計葉子數
			{
				count++;
			}
		}
		else if (leaf == 1) //當二叉樹隻有右子樹或左子樹
		{
			if (rt->lchild != NULL && rt->rchild == NULL) //隻有左子樹
			{
				if (p)
				{
					if (p != NULL)
					{
						push(ls, p);//将二叉樹的非空節點壓入棧中
					}
					p = p->lchild;//周遊左子樹
				}
				else
				{
					pop(ls, q);//彈出棧中的非空二叉樹節點
					cout << q->data << " "; //輸出彈出的二叉樹節點的資料
					if (q == root) //回到根節點時結束函數調用
					{
						free(ls);
						return;
					}
				}
			}
			else if (rt->rchild != NULL && rt->lchild == NULL) //隻有右子樹
			{
				if (p)
				{
					if (p != NULL)
					{
						push(ls, p);//将二叉樹的非空節點壓入棧中
					}
					p = p->rchild;//周遊右子樹
				}
				else
				{
					pop(ls, q);//彈出棧中的非空二叉樹節點
					cout << q->data << " ";//輸出彈出的二叉樹節點的資料
					if (q == root)//回到根節點時結束函數調用
					{
						free(ls);
						return;
					}
				}
			}
		}
	}
}
//後序遞歸算法
void rLRD(BTree rt)
{
	if (rt)
	{
		rLRD(rt->lchild);//先周遊左子樹
		rLRD(rt->rchild);//在周遊右子樹
		cout << rt->data << " "; //最後輸出根節點
	}
}
//後序非遞歸算法
void LRD(BTree rt)
{
	LinkStack ls;
	BTree cur, pre;
	InitLS(ls);
	if (rt == NULL)
	{
		cout << "樹為空" << endl;
		return;
	}
	//二叉樹前一個節點
	pre = NULL;
	//二叉樹目前節點
	cur = NULL;
	push(ls, rt);//先把根節點壓入棧中
	while (!stackempty(ls))
	{
		cur = NULL;
		gettop(ls, cur);
		if ((cur->lchild == NULL && cur->rchild == NULL) || (pre != NULL && (pre == cur->lchild || pre == cur->rchild)))
		{
			cout << cur->data << " "; //按照彈棧次序輸出目前二叉樹節點的資料
			if (cur == root)//如果已到根節點，結束函數調用
			{
				free(ls);
				return;
			}
			pre = cur;
			pop(ls, cur);
		}
		else
		{
			if (cur->rchild != NULL)
			{
				push(ls, cur->rchild);//再周遊右子樹，将右子樹節點壓棧
			}
			if (cur->lchild != NULL)
			{
				push(ls, cur->lchild);//最後周遊左子樹，将左子樹節點壓棧
			}
		}
	}
}
//使用遞歸求二叉樹的深度
int Depth(BTree rt)
{
	int deep = 0;
	if (rt)
	{
		int leftdeep = Depth(rt->lchild);
		int rightdeep = Depth(rt->rchild);
		deep = leftdeep >= rightdeep ? leftdeep + 1 : rightdeep + 1;
	}
	return deep;
}
//=======================================
int main()
{
	//int a[] = { 21, 2, 3, 4, 27, 8, 10 };
	cout << "===============================================================" << endl;
	cout << "\t\t二叉樹構造規則" << endl;
	cout << "采用先序規則構造二叉樹，先根節點後左節點在右節點" << endl;
	cout << "如果輸入的是整數 -1， \n則表示其前面剛輸入的正整數的左或右子樹為空。"
		<< "\n數組裡最後出現的數字0 \n表示構成該樹的所有正整數已輸入完畢。" << endl;
	cout << "============================================================" << endl;
	BTree tree = new BitNode;
	createBiTreeNonRecursive(tree);
	if (tree != NULL)
	{
		int size1 = node(tree);
		leafCount(tree);
		cout << "先序遞歸周遊二叉樹：" << endl;
		rDLR(tree);
		cout << endl;
		cout << "先序非遞歸周遊二叉樹：" << endl;
		DLR(tree);
		cout << endl;
		cout << "中序遞歸周遊二叉樹：" << endl;
		rLDR(tree);
		cout << endl;
		cout << "中序非遞歸周遊二叉樹：" << endl;
		LDR(tree);
		cout << endl;
		cout << "後序遞歸周遊二叉樹:" << endl;
		rLRD(tree);
		cout << endl;
		cout << "後序非遞歸周遊二叉樹：" << endl;
		LRD(tree);
		cout << endl;
		cout << "該二叉樹的葉子結點的數目：";
		cout << leaf << endl;
		int depth = Depth(tree);
		cout << "該二叉樹的深度：" << depth << endl;
		cout << "該二叉樹總節點數目：" << size1 << endl;
	}
	else
	{
		cout << "樹建立失敗！" << endl;
	}
	return 0;
}

輸出如下：

===============================================================
                二叉樹構造規則
采用先序規則構造二叉樹，先根節點後左節點在右節點
如果輸入的是整數 -1，
則表示其前面剛輸入的正整數的左或右子樹為空。
數組裡最後出現的數字0
表示構成該樹的所有正整數已輸入完畢。
============================================================
請按照構造規則輸入二叉樹的結點資料：
5 4 -1 3 2 -1 -1 1 -1 -1 6 -1 7 8 -1 -1 9 -1 -1 0
先序遞歸周遊二叉樹：
5 4 3 2 1 6 7 8 9
先序非遞歸周遊二叉樹：
5 4 3 2 1 6 7 8 9
中序遞歸周遊二叉樹：
4 2 3 1 5 6 8 7 9
中序非遞歸周遊二叉樹：
4 2 3 1 5 6 8 7 9
後序遞歸周遊二叉樹:
2 1 3 4 8 9 7 6 5
後序非遞歸周遊二叉樹：
2 1 3 4 8 9 7 6 5
該二叉樹的葉子結點的數目：4
該二叉樹的深度：4
該二叉樹總節點數目：9

四、二叉樹的周遊

二叉樹的周遊有 先序周遊、中序周遊、後序周遊和層次周遊。 其中，前三者的命名是根據什麼時候通路根節點而命名的。

1、先序周遊

所謂先序周遊，是指逐個通路二叉樹的節點時， 先通路根節點 ，然後 先序周遊左子樹 ，最後 先序周遊右子樹
。歸納起來就是三個不斷循環的步驟：

1）通路根節點；

2）先序周遊左子樹；

3）先序周遊右子樹。

用代碼描述如下：

void rDLR(BTree rt)
{
	if (rt)
	{
		cout << rt->data << " "; //先輸出根節點
		rDLR(rt->lchild); //再周遊左子樹
		rDLR(rt->rchild);//最後周遊右子樹
	}
}

這裡先用最容易實作的遞歸算法進行先序周遊。

2、中序周遊

顧名思義，此種周遊并沒有一開始就通路根節點，而是先左，再根，最後右。

1）中序周遊左子樹；

2）通路根節點；

3）中序周遊右子樹。

用遞歸算法描述如下：

void rLDR(BTree rt)
{
	if (rt)
	{
		rLDR(rt->lchild);//先周遊左子樹
		cout << rt->data << " ";//再輸出根節點
		rLDR(rt->rchild);//最後周遊右子樹
	}
}

3、後序周遊

後序周遊的步驟如下：

1）後序周遊左子樹；

2）後序周遊右子樹；

3）通路根節點。

算法函數如下：

//後序遞歸算法
void rLRD(BTree rt)
{
	if (rt)
	{
		rLRD(rt->lchild);//先周遊左子樹
		rLRD(rt->rchild);//在周遊右子樹
		cout << rt->data << " "; //最後輸出根節點
	}
}

4、三序周遊的非遞歸算法

前面所用的都是通過遞歸函數實作先序周遊、中序周遊和後序周遊，所有遞歸算法都可以利用棧進行解遞歸，以先序周遊為例進行解遞歸。

//===========非遞歸先序周遊
void DLR(BTree rt)
{
	LinkStack ls;
	BTree p = new BitNode;
	BTree q = new BitNode;
	p = rt;
	int count = 0;
	InitLS(ls);
	if (p == NULL)
	{
		cout << "樹空" << endl;
		return;
	}
	while (p || !stackempty(ls))
	{
		if (count == leaf)  //當目前二叉樹節點是二叉樹最後一個葉子節點時 ，無需後續操作，結束函數調用
		{
			free(ls);
			return;
		}
		if (p)
		{
			if (p != NULL)
			{
				push(ls, p); //将二叉樹的非空節點壓入棧中
			}
			cout << p->data << " "; //先輸出根節點
			p = p->lchild; //再周遊左子樹
		}
		else
		{
			pop(ls, q); //彈出棧中的非空二叉樹節點
			p = q->rchild; //最後周遊右子樹
		}
		if (IsLeaf(q)) //累計葉子數
		{
			count++;
		}
	}
}

首先建立一個節點為二叉樹結點的鍊棧。
目前節點或鍊棧非空時循環以下步驟：

1）如果目前節點非空，輸出目前節點的資料值，并壓入棧中；

2）如果目前節點為空，從棧中彈出棧頂元素，并将剛剛彈出的棧頂元素的右孩子賦為目前節點。
中序周遊和後序周遊的解遞歸也差不多是這個步驟，訓示通路目前節點的時間不一樣。

5、層次周遊

層次周遊，即 從根節點到葉子節點按層次增序方向從上到下、從左到右通路二叉樹的每個結點。
進行層次周遊需要借助隊列，算法步驟如下：

1）先将根節點入隊，然後出隊，通路出隊節點；

2）若有左子樹，則将左子樹根節點入隊；若有右子樹，則将右子樹根節點入隊；

3）然後出隊，通路出隊節點

4）重複上述步驟。

層次周遊的代碼如下：

//=======================================
// 層次周遊
typedef struct QueueNode
{
	BTree elem;
	QueueNode* next;
};
typedef struct LinkQueue
{
	QueueNode* front, * rear;
};
bool initQueue(LinkQueue& q)
{
	q.front = q.rear = new QueueNode;
	q.front->next = NULL;
	return true;
}
void EnQueue(LinkQueue& q, BTree e)
{
	QueueNode* s = new QueueNode;
	s->elem = e;
	s->next = NULL;
	q.rear->next = s;
	q.rear = s;
}
bool DeQueue(LinkQueue& q, BTree& e)
{
	if (q.front == q.rear) return false;
	QueueNode* p = q.front->next;
	e = p->elem;
	q.front->next = p->next;
	if (q.rear == p)
		q.rear = q.front;
	free(p);
	return true;
}
bool IsEmpty(LinkQueue q)
{
	if (q.rear == q.front)
		return true;
	return false;
}
void vist(BTree e)
{
	cout << e->data << " ";
}
void LevelOrder(BTree T)
{
	LinkQueue Q;
	initQueue(Q);
	BTree p;
	EnQueue(Q, T);
	while (!IsEmpty(Q))
	{
		DeQueue(Q, p);
		vist(p);
		if (p->lchild != NULL)
			EnQueue(Q, p->lchild);
		if (p->rchild != NULL)
			EnQueue(Q, p->rchild);
	}
}

6、周遊序列的應用

6.1、确定二叉樹

由二叉樹的先序周遊序列和中序周遊序列可以唯一确定一棵二叉樹。
由二叉樹的後序周遊序列和中序周遊序列可以唯一确定一棵二叉樹。
由二叉樹的層序周遊序列和中序周遊序列可以唯一确定一棵二叉樹。
在先序周遊序列中，第一個結點一定是二叉樹的根結點；而在中序周遊中，根結點必然将中序序列分割成兩個子序列，前一個子序列是根結點的左子樹的中序序列，後一個子序列是根結點的右子樹的中序序列。根據這兩個子序列，在先序序列中找到對應的左子序列和右子序列。在先序序列中，左子序列的第一個結點是左子樹的根結點，右子序列的第一個結點是右子樹的根結點。如此遞歸地進行下去，便能唯一地确定這棵二叉樹。

6.3、其他應用

先序周遊序列建立二叉連結清單。
複制二叉樹。
計算二叉樹深度。
統計二叉樹節點個數。

資料結構學習筆記之C++實作二叉樹一、樹二、二叉樹三、二叉樹實作四、二叉樹的周遊

二叉樹

一、樹

1、定義與特點

2、相關術語

3、性質

4、樹節點與度之間的關系

二、二叉樹

1、定義

2、與度為 2 的有序樹的差別

3、特殊二叉樹

3.1、滿二叉樹

3.2、完全二叉樹

3.3、二叉排序樹

3.4、平衡二叉樹

4、性質

5、存儲結構

6、基本操作

三、二叉樹實作

四、二叉樹的周遊

1、先序周遊

2、中序周遊

3、後序周遊

4、三序周遊的非遞歸算法

5、層次周遊

6、周遊序列的應用

6.1、确定二叉樹

6.3、其他應用

繼續閱讀