《機器學習》 2.5 偏差與方差 - 周志華
-
偏差與方差分别是用于衡量一個模型泛化誤差的兩個方面
- 模型的偏差,指的是模型預測的期望值與真實值之間的差;
- 模型的方差,指的是模型預測的期望值與預測值之間的差平方和;
- 在監督學習中,模型的泛化誤差可分解為偏差、方差與噪聲之和。
- 偏差用于描述模型的拟合能力;方差用于描述模型的穩定性。
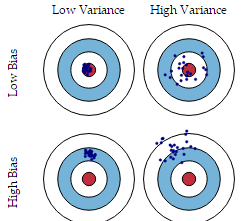
機器學習---偏差VS方差
1 原因
- 偏差通常是由于我們對學習算法做了錯誤的假設,或者模型的複雜度不夠;
- 比如真實模型是一個二次函數,而我們假設模型為一次函數,這就會導緻偏差的增大(欠拟合);
- 由偏差引起的誤差通常在訓練誤差上就能展現,或者說訓練誤差主要是由偏差造成的
- 方差通常是由于模型的複雜度相對于訓練集過高導緻的;
- 比如真實模型是一個簡單的二次函數,而我們假設模型是一個高次函數,這就會導緻方差的增大(過拟合);
- 由方差引起的誤差通常展現在測試誤差相對訓練誤差的增量上。
2 深度學習
- 神經網絡的拟合能力非常強,是以它的訓練誤差(偏差)通常較小;
- 但是過強的拟合能力會導緻較大的方差,使模型的測試誤差(泛化誤差)增大;
- 是以深度學習的核心工作之一就是研究如何降低模型的泛化誤差,這類方法統稱為正則化方法。
3 偏差/方差 與 Boosting/Bagging
- 簡單來說,Boosting 能提升弱分類器性能的原因是降低了偏差;Bagging 則是降低了方差;
- Boosting 方法:
- Boosting 的基本思路就是在不斷減小模型的訓練誤差(拟合殘差或者加大錯類的權重),加強模型的學習能力,進而減小偏差;
- 但 Boosting 不會顯著降低方差,因為其訓練過程中各基學習器是強相關的,缺少獨立性。
- Bagging 方法:
- 對 n 個獨立不相關的模型預測結果取平均,方差是原來的 1/n;
- 假設所有基分類器出錯的機率是獨立的,超過半數基分類器出錯的機率會随着基分類器的數量增加而下降。
- 泛化誤差、偏差、方差、過拟合、欠拟合、模型複雜度(模型容量)的關系圖:
機器學習---偏差VS方差
4 計算公式
-
記在訓練集 D 上學得的模型為
f ( x ; D ) f(x; D) f(x;D)
模型的期望預測為
f ^ ( x ) = E D [ f ( x ; D ) ] \hat{f}(\boldsymbol{x})=\mathbb{E}_D[f(\boldsymbol{x};D)] f^(x)=ED[f(x;D)]
-
偏差(Bias)
b i a s 2 ( x ) = ( f ^ ( x ) − y ) 2 bias^2(\boldsymbol{x})=(\hat{f}(\boldsymbol{x})-y)^2 bias2(x)=(f^(x)−y)2
偏差度量了學習算法的期望預測與真實結果的偏離程度,即刻畫了學習算法本身的拟合能力;
- 噪聲則表達了在目前任務上任何學習算法所能達到的期望泛化誤差的下界,即刻畫了學習問題本身的難度。
- “偏差-方差分解”表明模型的泛化能力是由算法的能力、資料的充分性、任務本身的難度共同決定的。
5 偏差與方差的權衡(過拟合與模型複雜度的權衡)
- 給定學習任務,
- 當訓練不足時,模型的拟合能力不夠(資料的擾動不足以使模型産生顯著的變化),此時偏差主導模型的泛化誤差;
- 随着訓練的進行,模型的拟合能力增強(模型能夠學習資料發生的擾動),此時方差逐漸主導模型的泛化誤差;
- 當訓練充足後,模型的拟合能力過強(資料的輕微擾動都會導緻模型産生顯著的變化),此時即發生過拟合(訓練資料自身的、非全局的特征也被模型學習了)
- 偏差和方差的關系和模型容量(模型複雜度)、欠拟合和過拟合的概念緊密相聯
機器學習---偏差VS方差 - 當模型的容量增大(x 軸)時, 偏差(用點表示)随之減小,而方差(虛線)随之增大
-
沿着 x軸存在最佳容量,小于最佳容量會呈現欠拟合,大于最佳容量會導緻過拟
合。
Reference
Understanding the Bias-Variance Tradeoff
機器學習中的Bias(偏差),Error(誤差),和Variance(方差)有什麼差別和聯系? - 知乎