一、過拟合的本質及現象
過拟合是指模型隻過分地比對特定訓練資料集,以至于對訓練集外資料無良好地拟合及預測。其本質原因是模型從訓練資料中學習到了一些統計噪聲,即這部分資訊僅是局部資料的統計規律,該資訊沒有代表性,在訓練集上雖然效果很好,但未知的資料集(測試集)并不适用。
1.1 評估拟合效果
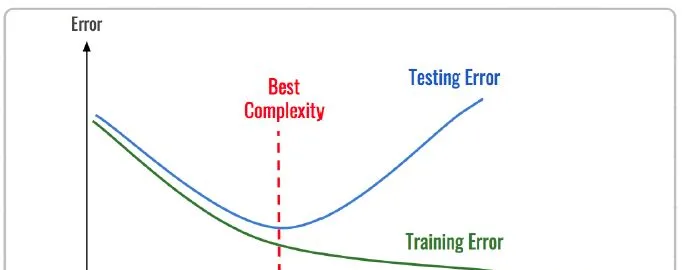
通常由訓練誤差及測試誤差(泛化誤差)評估模型的學習程度及泛化能力。欠拟合時訓練誤差和測試誤差在均較高,随着訓練時間及模型複雜度的增加而下降。在到達一個拟合最優的臨界點之後,訓練誤差下降,測試誤差上升,這個時候就進入了過拟合區域。它們的誤差情況差異如下表所示:
1.2 拟合效果的深入分析
對于拟合效果除了通過訓練、測試的誤差估計其泛化誤差及判斷拟合程度之外,我們往往還希望了解它為什麼具有這樣的泛化性能。統計學常用“偏差-方差分解”(bias-variance decomposition)來分析模型的泛化性能:泛化誤差為偏差+方差+噪聲之和。
噪聲(ε) 表達了在目前任務上任何學習算法所能達到的泛化誤差的下界,即刻畫了學習問題本身(客觀存在)的難度。
偏差(bias) 是指用所有可能的訓練資料集訓練出的所有模型的輸出值與真實值之間的差異,刻畫了模型的拟合能力。偏差較小即模型預測準确度越高,表示模型拟合程度越高。
方差(variance) 是指不同的訓練資料集訓練出的模型對同預測樣本輸出值之間的差異,刻畫了訓練資料擾動所造成的影響。方差較大即模型預測值越不穩定,表示模型(過)拟合程度越高,受訓練集擾動影響越大。
如下用靶心圖形象表示不同方差及偏差下模型預測的差異:
偏差越小,模型預測值與目标值差異越小,預測值越準确;
方差越小,不同的訓練資料集訓練出的模型對同預測樣本預測值差異越小,預測值越集中;
“偏差-方差分解” 說明,模型拟合過程的泛化性能是由學習算法的能力、資料的充分性以及學習任務本身的難度所共同決定的。
當模型欠拟合時:模型準确度不高(高偏差),受訓練資料的擾動影響較小(低方差),其泛化誤差大主要由高的偏差導緻。
當模型過拟合時:模型準确度較高(低偏差),模型容易學習到訓練資料擾動的噪音(高方差),其泛化誤差大由高的方差導緻。
實踐中通常欠拟合不是問題,可以通過使用強特征及較複雜的模型提高學習的準确度。而解決過拟合,即如何減少泛化誤差,提高泛化能力,通常才是優化模型效果的重點。
二、如何解決過拟合
2.1 解決思路
上文說到學習統計噪聲是過拟合的本質原因,而模型學習是以經驗損失最小化,現實中學習的訓練資料難免有統計噪音的。一個簡單的思路,通過提高資料量數量或者品質解決統計噪音的影響:
- 通過足夠的資料量就可以有效區分哪些資訊是片面的,然而現實情況資料通常都很有限的。
- 通過提高資料的品質,可以結合先驗知識加工特征以及對資料中噪聲進行剔除(噪聲如訓練集有個“使用者編号尾數是否為9”的特征下,偶然有正樣本的占比很高的現象,而憑業務知識了解這個特征是沒有意義的噪聲,就可以考慮剔除)。但這樣,一來過于依賴人工,人工智障?二來先驗領域知識過多的引入,如果領域知識有誤,不也是噪聲。
當資料層面的優化有限,接下來登場主流的方法——正則化政策。
在以(可能)增加經驗損失為代價,以降低泛化誤差為目的,解決過拟合,提高模型泛化能力的方法,統稱為正則化政策。
2.2 常見的正則化政策及原理
本節嘗試以不一樣的角度去了解正則化政策,歡迎留言交流。
正則化政策經常解讀為對模型結構風險的懲罰,崇尚簡單模型。并不盡然!如前文所講學到統計噪聲是過拟合的本質原因,是以模型複雜度容易引起過拟合(隻是影響因素)。然而工程中,對于困難的任務需要足夠複雜的模型,這種情況縮減模型複雜度不就和“減智商”一樣?是以,通常足夠複雜且有正則化的模型才是我們追求的,且正則化不是隻有減少模型容量這方式。
機器學習是從訓練集經驗損失最小化為學習目标,而學習的訓練集裡面不可避免有統計噪聲。除了提高資料品質和數量方法,我們不也可以在模型學習的過程中,給一些指導性的先驗假設(即根據一些已知的知識對參數的分布進行一定的假設),幫助模型更好避開一些“噪聲”的資訊并關注到本質特征,更好地學習模型結構及參數。這些指導性的先驗假設,也就是正則化政策,常見的正則化政策如下:
L2 正則化
L2 參數正則化 (也稱為嶺回歸、Tikhonov 正則) 通常被稱為權重衰減 (weight decay),是通過向⽬标函數添加⼀個正則項 Ω(θ) ,使權重更加接近原點,模型更為簡單(容器更小)。從貝葉斯角度,L2的限制項可以視為模型參數引入先驗的高斯分布(參見Bob Carpenter的 Lazy Sparse Stochastic Gradient Descent for Regularized )
對帶L2目标函數的模型參數更新權重,ϵ學習率:
從上式可以看出,加⼊權重衰減後會導緻學習規則的修改,即在每步執⾏梯度更新前先收縮權重 (乘以 1 − ϵα ),有權重衰減的效果,但是w比較不容易為0。
L1 正則化
L1 正則化(Lasso回歸)是通過向⽬标函數添加⼀個參數懲罰項 Ω(θ),為各個參數的絕對值之和。從貝葉斯角度,L1的限制項也可以視為模型參數引入拉普拉斯分布。
對帶L1目标函數的模型參數更新權重(其中 sgn(x) 為符号函數,取參數的正負号):
可見,在-αsgn(w)項的作用下, w各元素每步更新後的權重向量都會平穩地向0靠攏,w的部分元素容易為0,造成稀疏性。模型更簡單,容器更小。
對比L1,L2,兩者的有效性都展現在限制了模型的解空間w,降低了模型複雜度(容量)。L2範式限制具有産生平滑解的效果,沒有稀疏解的能力,即參數并不會出現很多零。假設我們的決策結果與兩個特征有關,L2正則傾向于綜合兩者的影響(可以看作符合bagging多釋準則的先驗),給影響大的特征賦予高的權重;而L1正則傾向于選擇影響較大的參數,而盡可能舍棄掉影響較小的那個( 可以看作符合了“奧卡姆剃刀定律--如無必要勿增實體”的先驗)。在實際應用中 L2正則表現往往會優于 L1正則,但 L1正則會壓縮模型,降低計算量。
在Keras中,可以使用regularizers子產品來在某個層上應用L1及L2正則化,如下代碼:
from keras import regularizers
model.add(Dense(64, input_dim=64,
kernel_regularizer=regularizers.l1_l2(l1=α1, l2=α2) # α為超參數懲罰系數 earlystop
earlystop(早停法)可以限制模型最小化代價函數所需的訓練疊代次數,如果疊代次數太少,算法容易欠拟合(方差較小,偏差較大),而疊代次數太多,算法容易過拟合(方差較大,偏差較小),早停法通過确定疊代次數解決這個問題。
earlystop可認為是将優化過程的參數空間限制在初始參數值 θ0 的小鄰域内(Bishop 1995a 和Sjöberg and Ljung 1995 ),在這角度上相當于L2正則化的作用。
在Keras中,可以使用callbacks函數實作早期停止,如下代碼:
from keras.callbacks import EarlyStopping
callback =EarlyStopping(monitor='loss', patience=3)
model = keras.models.Sequential([tf.keras.layers.Dense(10)])
model.compile(keras.optimizers.SGD(), loss='mse')
history = model.fit(np.arange(100).reshape(5, 20), np.zeros(5),
epochs=10, batch_size=1, callbacks=[callback],
verbose=0) 資料增強
資料增強是提升算法性能、滿足深度學習模型對大量資料的需求的重要工具。資料增強通過向訓練資料添加轉換或擾動來增加訓練資料集。資料增強技術如水準或垂直翻轉圖像、裁剪、色彩變換、擴充和旋轉(此外還有生成模型僞造的對抗樣本),通常應用在視覺表象和圖像分類中,通過資料增強有助于更準确的學習到輸入資料所分布的流形(manifold)。
在keras中,你可以使用ImageDataGenerator來實作上述的圖像變換資料增強,如下代碼:
from keras.preprocessing.image import ImageDataGenerator
datagen = ImageDataGenerator(horizontal_flip=True)
datagen.fit(train) 引入噪聲
與清洗資料的噪音相反,引入噪聲也可以明顯增加神經網絡模型的魯棒性(很像是以毒攻毒)。對于某些模型而言,向輸入添加方差極小的噪聲等價于對權重施加範數懲罰 (Bishop, 1995a,b)。常用有三種方式:
- 在輸入層引入噪聲,可以視為是一種資料增強的方法。
- 在模型權重引入噪聲
這項技術主要用于循環神經網絡 (Jim et al., 1996; Graves, 2011)。向網絡權重注入噪聲,其代價函數等于無噪聲注入的代價函數加上一個與噪聲方差成正比的參數正則化項。
- 在标簽引入噪聲
原實際标簽y可能多少含有噪聲,當 y 是錯誤的,直接使用0或1作為标簽,對最大化 log p(y | x)效果變差。另外,使用softmax 函數和最大似然目标,可能永遠無法真正輸出預測值為 0 或 1,是以它會繼續學習越來越大的權重,使預測更極端。使用标簽平滑的優勢是能防止模型追求具體機率又不妨礙正确分類。如标簽平滑 (label smoothing) 基于 k 個輸出的softmax 函數,把明确分類 0 和 1 替換成 ϵ /(k−1) 和 1 − ϵ,對模型進行正則化。
半監督學習
半監督學習思想是在标記樣本數量較少的情況下,通過在模型訓練中直接引入無标記樣本,以充分捕捉資料整體潛在分布,以改善如傳統無監督學習過程盲目性、監督學習在訓練樣本不足導緻的學習效果不佳的問題 。
依據“流形假設——觀察到的資料實際上是由一個低維流形映射到高維空間上的。由于資料内部特征的限制,一些高維中的資料會産生次元上的備援,實際上隻需要比較低的次元就能唯一地表示”,無标簽資料相當于提供了一種正則化(regularization),有助于更準确的學習到輸入資料所分布的流形(manifold),而這個低維流形就是資料的本質表示。
多任務學習
多任務學習(Caruana, 1993) 是通過合并幾個任務中的樣例(可以視為對參數施加的軟限制)來提高泛化的一種方法,其引入一個先驗假設:這些不同的任務中,能解釋資料變化的因子是跨任務共享的。常見有兩種方式:基于參數的共享及基于正則化的共享。
額外的訓練樣本以同樣的方式将模型的參數推向泛化更好的方向,當模型的一部分在任務之間共享時,模型的這一部分更多地被限制為良好的值(假設共享是合理的),往往能更好地泛化。
bagging
bagging是機器學習內建學習的一種。依據多釋準則,結合了多個模型(符合經驗觀察的假設)的決策達到更好效果。具體如類似随機森林的思路,對原始的m個訓練樣本進行有放回随機采樣,建構t組m個樣本的資料集,然後分别用這t組資料集去訓練t個的DNN,最後對t個DNN模型的輸出用權重平均法或者投票法決定最終輸出。
bagging 可以通過平滑效果降低了方差,并中和些噪聲帶來的誤差,是以有更高的泛化能力。
Dropout
Dropout是正則化技術簡單有趣且有效的方法,在神經網絡很常用。其方法是:在每個疊代過程中,以一定機率p随機選擇輸入層或者隐藏層的(通常隐藏層)某些節點,并且删除其前向和後向連接配接(讓這些節點暫時失效)。權重的更新不再依賴于有“邏輯關系”的隐藏層的神經元的共同作用,一定程度上避免了一些特征隻有在特定特征下才有效果的情況,迫使網絡學習更加魯棒(指系統的健壯性)的特征,達到減小過拟合的效果。這也可以近似為機器學習中的內建bagging方法,通過bagging多樣的的網絡結構模型,達到更好的泛化效果。
相似的還有Drop Connect ,它和 Dropout 相似的地方在于它涉及在模型結構中引入稀疏性,不同之處在于它引入的是權重的稀疏性而不是層的輸出向量的稀疏性。
在Keras中,我們可以使用Dropout層實作dropout,代碼如下:
from keras.layers.core import Dropout
model = Sequential([
Dense(output_dim=hidden1_num_units, input_dim=input_num_units, activation='relu'),
Dropout(0.25)
]) (end)
文章首發公衆号“算法進階”,更多原創文章敬請關注。