機器學習_總結篇_十大經典算法與算法選擇

一、 資料挖掘十大經典算法

最近寫了一些機器學習的文檔，對應資料挖掘經典算法，清單如下：

1. 聚類K-Means

​​《機器學習_基于距離的算法KNN與K-Means》​​

2. 關聯Apriori

​​《機器學習_規則與關聯規則模型Apriori、FP-Growth》​​

3. 最大期望EM

​​《機器學習_隐馬爾可夫模型HMM》​​

4. 決策樹DTree

​​《機器學習_決策樹與資訊熵》​​

5. CART: 分類與回歸樹

​​《機器學習_用樹回歸方法畫股票趨勢線》​​

6. 貝葉斯Bayes

​​《機器學習_統計模型之（一）貝葉斯公式》​​​​《機器學習_統計模型之（二）貝葉斯網絡》​​​​《機器學習_統計模型之（三）樸素貝葉斯》​​

7. 線性回歸logistic

​​《機器學習_最小二乘法，線性回歸與邏輯回歸》​​

8. 內建算法adaBoost

​​《機器學習_內建算法》​​

9. 支援向量機SVM

​​《機器學習_SVM支援向量機》​​

10. PageRank

（沒寫）

11. 其它（特征工程）

​​《機器學習_用SVD奇異值分解給資料降維》​​​​《機器學習_用PCA主成分分析給資料降維》​​

12. 總結

 資料挖掘是人工智能的一個分枝，基本覆寫了大部分機器學習算法。

 有了深度學習之後，這些算法大多被歸入淺層學習。至于是選擇深度學習還是淺層學習，主要還是要看具體問題。兩種學習也是強相關的，像在CNN和RNN的算法中其實也容入了淺層學習的很多想法。而HMM和GBDT看起來和深度學習也很相似。我覺得深度模型更值得借鑒的是它可以在多個層次同時調整。在內建淺層算法時，也可以參考。

二、 淺談算法選型

 以下是一些個人看法，希望在算法選型時給大家一些啟發。

1. 算法的分類

 從開始看第一本講算法書起，就希望能把算法歸類，或者能讓算法和問題類型對應起來。但好像并不這麼簡單。

 《機器學習》（Peter Flach著）把有學習模型分成三類：幾何模型，統計模型，邏輯模型。簡單地說，幾何模型就是計算執行個體間的距離；統計模型是對已知變量X與未知變量Y之間的依賴關系統計模組化；邏輯模型更偏重規則，每一種算法都被可被劃入其中一種至幾種分類。

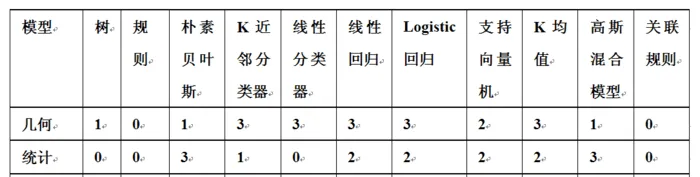
 雖然不能完全分開，但是遇到具體問題的時候，三選一總比十選一要容易得多。

2. 微調與重構

 羅曼羅蘭說：“大半的人在二十歲或三十歲上就死了。一過這個年齡，他們隻變了自己的影子”。這其實挺合理的。當一個基礎系統，很多上層都依賴于它時，任何修改都可能導緻上層多個系統的崩潰，是以一般系統達到一定規模之後，修改都以查缺補漏為主。一個系統停止更新了，基本也就看到天花闆了。

 微調總比重構來得容易，但效果也有限。以ImageNet比賽為例，每一次重大的進步都是因為加入了新結構，而微調和增加算力，效果都不特别特著。

 我們使用現成算法也有這個問題，比如用sklearn庫中的算法時，主要是調參，對調用者來說庫就是黑盒，沒法針對資料的特征做内部的修改，或者在内部嫁接多個算法。用庫，你能輕松地趕上大家的水準，但是很難突破。是以有時候，看一個資料挖掘比賽，前十名用的都是同一個算法，大家主要在比調參和特征工程。

3. 有監督、無監督與半監督

 确定有監督、無監督，是選擇算法的第一步。這兩種情況對應的算法完全不同，不過現在也常把聚類（無監督）放在有監督學習中使用（比如CNN）。

 強化學習是一種半監督學習，一般是根據規則模拟一些場景，用于訓練，比如利用左右互博的方式訓練下棋，自動駕駛，機器人等等，它可以作為一種有效的資料補充。

4. 精确與啟發

 精确模型對所有資料有效，往往用于預測（比如決策樹），而啟發模型對部分資料有效，往往用于篩選（比如規則模型）。

 具體選擇哪種模型，取決于已知資料帶有資訊量的多少。如果用屬性和結果做圖，發現大多數資料都是有規律的，就使精确模型。如果大多數都是噪音，隻有少量有價值的點（或者是稀疏的），最好能選用啟發模型，至少也要先把有序資料和無序資料分開。

5. 單模式與多模式

取得正确結果的路徑往往不止一條，就如同決策樹中的分枝，從這個角度看，處理複雜問題的時候，邏輯模型是必不可少的。

 對于多模式，像樸素貝葉斯，線性回歸這種簡單算法就不太适用了，有時候我們會使用內建算法，把幾種算法結合在一起。

 處理具體問題的時候，也需要先判斷這是單模式問題，還是多模式問題？單模式，可能傾向用幾何距離類的算法，多模式可能要考慮邏輯和統計類，內建算法，或者先看看能不能把資料拆分後再做進一步處理。

6. 總結與推理

 模型有時被劃分成判别式和生成式，判别式的訓練過程一般以總結為主，比如決策樹，線性拟合；而生成式中加入了一些推理，比如說關聯規則，一階規則，貝葉斯網絡等等。選算法時也要注意，是否需要機器推導。

7. 表面與隐藏

 隐馬爾可夫模型和神經網絡模型中都有隐藏層的概念，它闡釋出内在的關系，這類算法常對應一些比較複雜的問題。

8. 線性與非線性

 線性指量與量之間按比例、成直線的關系，在數學上可以了解為一階導數為常數的函數；非線性則指不按比例、不成直線的關系，一階導數不為常數。

 線性模型指一般線性模型，線性混合模型和廣義線性模型（先映射成線性模型，再做處理），比如線性拟合，logistic回歸，局部權重線性回歸，SVM都屬于線性類的模型。有的也能拟合曲線，但作用範圍有限。

 神經網絡的主要優點之一就是能解決非線性問題。

 線性模型和線性變換都是非常基本元素，算法中幾乎無處不在。一般線性模型用隻能處理簡單的問題，主要是和其它算法組合使用。

9. 相關性、組合與分解

 分析屬性間的關系對選擇算法也很重要，有時能看到屬性間有明顯的關系，比如圖像中每個像素與它上下左右的相鄰像素都相關，這時候我們使用神經網絡中的卷積來替代全連接配接。

 執行個體間也可能存在聯系，比如股票中漲跌幅就是兩日收盤價計算出來的，相比于收盤價，漲跌幅更具意義。

 另外，還有一些不太明顯的關系，可以通過分析特征的相關系數得到，并使用降維減小相關性和減少資料。

10. 連續與離散

 我們拿到的原始資料可能是連續的或是離散的，因為可以互相轉換，資料的類型倒不是大問題，不過轉換時，也需要注意一些細節。

 比如說連續資料離散化時，需要去考慮切分的方法，像等深、等寬分箱，切分視窗重疊等等，最好能先用直方圖分析一下資料的分布。

 離散值轉成連續值時也有一些問題，比如把：”男人”，“女人”與“孩子”，映射成0,1,2，那“男人”與“孩子”間的距離更大，這是明顯是不合理的，這時候可能需要把一個屬性拆成三個。

11. 資料儲存

 我們的思維中有多少是真正的思考，有多少是套路呢？如何把習得的套路儲存下來，以及重用呢？

 套路可能是決策樹規則，可能是神經網絡參數，可能是規則清單，又或是典型執行個體；還有一些學習得來的知識，怎麼把它們容入連接配接成更大的模型？

 對于人來講，最終得以儲存的可能是不可描述的經驗和可描述的規則，規則可以是經驗總結的，也可以是習得的，可以執行個體化，又可以加入進一步推導。它所涵蓋的可能是全部（樹模型），也可能是部分（規則模型），或者是一條主幹（線性拟合）加上一些例外（離群點）。

12. 問題類型

 下面看看常見的資料挖掘問題

i. 純資料的預測問題：

 通過各個特征值預測結果，比較流行使用GDBT和CNN算法。

ii. 關聯問題：

 如根據使用者的浏覽，收藏，購物，給使用者推薦，可能用到聚類，關聯規則。

iii. 複雜問題

 涉及一些組合問題，比如自動駕駛，機器人，需要處理一些沖突，均衡，常使用神經網絡，博弈算法，有時也用到增強學習。

iv. 專業領域的問題

 如圖像處理，音頻，自然語言處理，地圖資料，涉及專業領域的知識，需要分析資料的具體特點以選擇算法。

技術文章定時推送

請關注公衆号：算法學習分享

​