[原創]從1億個資料中找出前100個最大值

從一億個資料中找出前100個最大值

方法一：

> 建立一100個紅黑樹節點，将輸入前100個儲存進去，然後全部插入紅黑樹T

> 周遊剩下的所有輸入，對每一個輸入值，如果值大于紅黑樹中最小值，則删除最小值節點，然後修改被删除節點的值為目前輸入，然後插入紅黑樹。

複雜度為n*lg(m), n為輸入資料條數，m為輸出資料條數

方法二：将紅黑樹替換成最小堆，每插入一條資料，隻需要運作MIN_HEAPIFY即可。

實際運作結果來看，最小堆的方法更快。

方法一代碼如下，紅黑樹代碼參考https://blog.csdn.net/v2nero/article/details/19170987

#include "stdafx.h"
#include <iostream>
#include <set>
#include <inttypes.h>
#include "rb.h"
#include <time.h>



//#define	outputNum	100
//#define	inputNum	100000000

int main(int arc, char *arv[])
{
	if (arc != 3) {
		printf("head100 input_num output_num\n");
		return 1;
	}
	int inputNum = atoi(arv[1]);
	int outputNum = atoi(arv[2]);
	rb_tree_t T;
	ia_rb_tree_init(&T);

	rb_tree_node_t *nodes = new rb_tree_node_t[outputNum];
	memset(nodes, 0, sizeof(rb_tree_node_t)*outputNum);

	clock_t clock_s = 0, clock_e = 0;
	clock_s = clock();

	for (int i = 0; i < outputNum; ++i) {
		nodes[i].key = 0;
	}

	for (int i = 0; i < inputNum; ++i) {
		if (i < outputNum) {
			nodes[i].key = i;
			ia_rb_tree_insert(&T, &nodes[i]);
		} else {
			rb_tree_node_t *node = ia_rb_tree_minnode(&T);
			if (i > node->key) {
				ia_rb_tree_delete(&T, node);
				node->key = i;
				ia_rb_tree_insert(&T, node);
			}
		}
	}

	clock_e = clock();
	double duration = (clock_e - clock_s)/CLOCKS_PER_SEC;
	printf("\n%2.3f seconds\n", duration);

	//ia_rb_tree_inorder_walk(&T, T.root, NULL);
	delete[] nodes;

	return 0;
}
           

結果似乎不是特别理想，可能是紅黑樹操作常量乘積過大吧

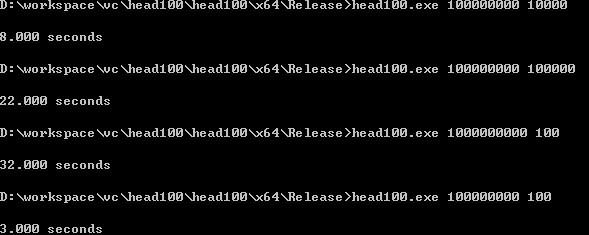
CPU: 

Linux -O3編譯運作結果

[email protected]:~/ws/ia/head100$ ./head100_rb 1000000000 100

45.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_rb 100000000 100

4.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_rb 100000000 1000

6.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_rb 100000000 10000

12.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_rb 100000000 100000

22.000 seconds
           

方法二代碼如下:

#include "common.h"
 
typedef struct _heap_t {
	int length;	//array length
	int size;	//heap size
	int *data;
} heap_t;
 
#define PARENT(i) ((i-1)/2)
#define LEFT(i) (2*i + 1)
#define RIGHT(i) (2*i + 2)
 
 
//MIN-HEAPIFY
void MIN_HEAPIFY(heap_t *A, int i)
{
	int l = LEFT(i);
	int r = RIGHT(i);
	int smallest = 0;
	int tmp = 0;
 
	if (l < A->size &&
	    A->data[l] < A->data[i]) {
		smallest = l;
	} else {
		smallest = i;
	}
 
	if (r < A->size &&
	    A->data[r] < A->data[smallest]) {
		smallest = r;
	}
 
	if (smallest != i) {
		tmp = A->data[smallest];
		A->data[smallest] = A->data[i];
		A->data[i] = tmp;
		MIN_HEAPIFY(A, smallest);
	}
}


int Head100(int arc, const char *arv[]) {
	if (arc != 3) {
		printf("head100 input_num output_num\n");
		return 1;
	}
	int inputNum = atoi(arv[1]);
	int outputNum = atoi(arv[2]);
	heap_t heap;
	heap.size = outputNum;
	heap.length = outputNum;
	heap.data = new int[outputNum];
	//memset(heap.data, 0xff, sizeof(int)*outputNum);
	for (int i = 0; i < outputNum; ++i) {
		heap.data[i] = INT_MIN;
	}
	
	clock_t clock_s = 0, clock_e = 0;
	clock_s = clock();

	for (int i = 0; i < inputNum; ++i) {
		if (i > heap.data[0]) {
			heap.data[0] = i;
			MIN_HEAPIFY(&heap, 0);
		}
	}

	clock_e = clock();
	double duration = (clock_e - clock_s)/CLOCKS_PER_SEC;
	printf("\n%2.3f seconds\n", duration);

#if 0
	for (int i = 0; i < outputNum; ++i) {
		TRACE("%d ", heap.data[i]);
	}
#endif

	delete []heap.data;

	return 0;
}

 
int main(int arc, const char *arv[])
{
	return Head100(arc, arv);	
}
           

Linux -O3運作速度如下

[email protected]:~/ws/ia/head100$ ./head100_heap 100000000 100

2.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_heap 100000000 1000

3.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_heap 100000000 10000

5.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_heap 100000000 100000

6.000 seconds
[email protected]:~/ws/ia/head100$ ./head100_heap 1000000000 100

22.000 seconds