Numpy練習題-鍛煉手寫機器學習模型的能力

Numpy是一個用python實作的科學計算的擴充程式庫，包括：

1、一個強大的N維數組對象Array；

2、比較成熟的（廣播）函數庫；

3、用于整合C/C++和Fortran代碼的工具包；

4、實用的線性代數、傅裡葉變換和随機數生成函數。numpy和稀疏矩陣運算包scipy配合使用更加友善。

NumPy（Numeric Python）提供了許多進階的數值程式設計工具，如：矩陣資料類型、矢量處理，以及精密的運算庫。專為進行嚴格的數字處理而産生。多為很多大型金融公司使用，以及核心的科學計算組織如：Lawrence Livermore，NASA用其處理一些本來使用C++，Fortran或Matlab等所做的任務。

本文整理了一個Numpy的練習題，總結了Numpy的常用操作，可以測試下自己對Numpy的掌握程度，有答案哦。 

下載下傳位址：

https://github.com/fengdu78/Data-Science-Notes/tree/master/2.numpy/numpy_exercises

試題目錄

• Array creation routines（數組建立）
• Array manipulation routines（數組操作）
• String operations（字元串操作）
• Numpy-specific help functions（Numpy特定幫助函數）
• Input and output（輸入和輸出）
• Linear algebra（線性代數）
• Discrete Fourier Transform（離散傅裡葉變換）
• Logic functions（邏輯函數）
• Mathematical functions（數學函數）
• Random sampling (numpy.random)（随機抽樣）
• Set routines（集合操作）
• Sorting, searching, and counting（排序、搜尋和計數）
• Statistics（統計）

試題内容

試題分為13個練習，每個練習分為兩個ipynb檔案，檔案名帶

_Solutions

的是帶答案的檔案，建議初學者先練習下不帶答案的檔案,做不出來再看看答案。

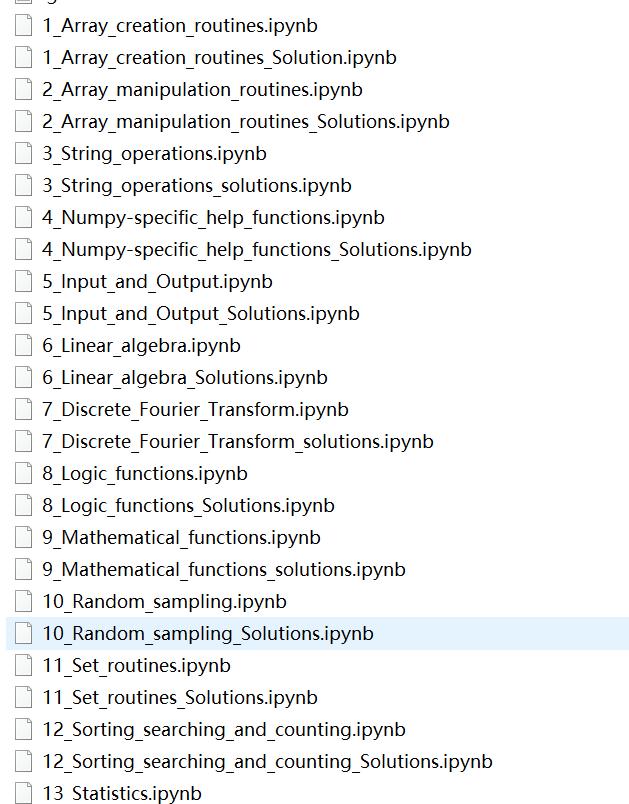
試題樣例

Linear algebra

import numpy as np
           

np.__version__
           

'1.11.2'
           

Matrix and vector products

Q1. Predict the results of the following code.

x = [1,2]
y = [[4, 1], [2, 2]]
print np.dot(x, y)
print np.dot(y, x)
print np.matmul(x, y)
print np.inner(x, y)
print np.inner(y, x)
           

[8 5]
[6 6]
[8 5]
[6 6]
[6 6]
           

Q2. Predict the results of the following code.

x = [[1, 0], [0, 1]]
y = [[4, 1], [2, 2], [1, 1]]
print np.dot(y, x)
print np.matmul(y, x)

           

[[4 1]
 [2 2]
 [1 1]]
[[4 1]
 [2 2]
 [1 1]]
           

Q3. Predict the results of the following code.

x = np.array([[1, 4], [5, 6]])
y = np.array([[4, 1], [2, 2]])
print np.vdot(x, y)
print np.vdot(y, x)
print np.dot(x.flatten(), y.flatten())
print np.inner(x.flatten(), y.flatten())
print (x*y).sum()
           

30
30
30
30
30
           

Q4. Predict the results of the following code.

x = np.array(['a', 'b'], dtype=object)
y = np.array([1, 2])
print np.inner(x, y)
print np.inner(y, x)
print np.outer(x, y)
print np.outer(y, x)
           

abb
abb
[['a' 'aa']
 ['b' 'bb']]
[['a' 'b']
 ['aa' 'bb']]
           

Decompositions

Q5. Get the lower-trianglular

L

in the Cholesky decomposition of x and verify it.

x = np.array([[4, 12, -16], [12, 37, -43], [-16, -43, 98]], dtype=np.int32)
L = np.linalg.cholesky(x)
print L
assert np.array_equal(np.dot(L, L.T.conjugate()), x)
           

[[ 2.  0.  0.]
 [ 6.  1.  0.]
 [-8.  5.  3.]]
           

Q6. Compute the qr factorization of x and verify it.

x = np.array([[12, -51, 4], [6, 167, -68], [-4, 24, -41]], dtype=np.float32)
q, r = np.linalg.qr(x)
print "q=\n", q, "\nr=\n", r
assert np.allclose(np.dot(q, r), x)
           

q=
[[-0.85714287  0.39428571  0.33142856]
 [-0.42857143 -0.90285712 -0.03428571]
 [ 0.2857143  -0.17142858  0.94285715]] 
r=
[[ -14.  -21.   14.]
 [   0. -175.   70.]
 [   0.    0.  -35.]]
           

Q7. Factor x by Singular Value Decomposition and verify it.

x = np.array([[1, 0, 0, 0, 2], [0, 0, 3, 0, 0], [0, 0, 0, 0, 0], [0, 2, 0, 0, 0]], dtype=np.float32)
U, s, V = np.linalg.svd(x, full_matrices=False)
print "U=\n", U, "\ns=\n", s, "\nV=\n", v
assert np.allclose(np.dot(U, np.dot(np.diag(s), V)), x)

           

U=
[[ 0.  1.  0.  0.]
 [ 1.  0.  0.  0.]
 [ 0.  0.  0. -1.]
 [ 0.  0.  1.  0.]] 
s=
[ 3.          2.23606801  2.          0.        ] 
V=
[[ 1.  0.  0.]
 [ 0.  1.  0.]
 [ 0.  0.  1.]]
           

Matrix eigenvalues

Q8. Compute the eigenvalues and right eigenvectors of x. (Name them eigenvals and eigenvecs, respectively)

x = np.diag((1, 2, 3))
eigenvals = np.linalg.eig(x)[0]
eigenvals_ = np.linalg.eigvals(x)
assert np.array_equal(eigenvals, eigenvals_)
print "eigenvalues are\n", eigenvals
eigenvecs = np.linalg.eig(x)[1]
print "eigenvectors are\n", eigenvecs
           

eigenvalues are
[ 1.  2.  3.]
eigenvectors are
[[ 1.  0.  0.]
 [ 0.  1.  0.]
 [ 0.  0.  1.]]
           

Q9. Predict the results of the following code.

print np.array_equal(np.dot(x, eigenvecs), eigenvals * eigenvecs)
           

True
           

Norms and other numbers

Q10. Calculate the Frobenius norm and the condition number of x.

x = np.arange(1, 10).reshape((3, 3))
print np.linalg.norm(x, 'fro')
print np.linalg.cond(x, 'fro')
           

16.8819430161
4.56177073661e+17
           

Q11. Calculate the determinant of x.

x = np.arange(1, 5).reshape((2, 2))
out1 = np.linalg.det(x)
out2 = x[0, 0] * x[1, 1] - x[0, 1] * x[1, 0]
assert np.allclose(out1, out2)
print out1
           

-2.0
           

Q12. Calculate the rank of x.

x = np.eye(4)
out1 = np.linalg.matrix_rank(x)
out2 = np.linalg.svd(x)[1].size
assert out1 == out2
print out1

           

4
           

Q13. Compute the sign and natural logarithm of the determinant of x.

x = np.arange(1, 5).reshape((2, 2))
sign, logdet = np.linalg.slogdet(x)
det = np.linalg.det(x)
assert sign == np.sign(det)
assert logdet == np.log(np.abs(det))
print sign, logdet

           

-1.0 0.69314718056
           

Q14. Return the sum along the diagonal of x.

x = np.eye(4)
out1 = np.trace(x)
out2 = x.diagonal().sum()
assert out1 == out2
print out1
           

4.0
           

Solving equations and inverting matrices

Q15. Compute the inverse of x.

x = np.array([[1., 2.], [3., 4.]])
out1 = np.linalg.inv(x)
assert np.allclose(np.dot(x, out1), np.eye(2))
print out1

           

[[-2.   1. ]
 [ 1.5 -0.5]]
           

其他資源

本站還發過不少關于Numpy的資源，歡迎收藏學習：

• 1.Numpy小抄表
• 2.Numpy100題
• 3.AI基礎-Numpy簡易入門

參考

• 作者：Kyubyong
• 來源：https://github.com/Kyubyong/numpy_exercises

下載下傳位址：

https://github.com/fengdu78/Data-Science-Notes/tree/master/2.numpy/numpy_exercises

往期精彩回顧



适合初學者入門人工智能的路線及資料下載下傳機器學習及深度學習筆記等資料列印機器學習線上手冊深度學習筆記專輯《統計學習方法》的代碼複現專輯
AI基礎下載下傳機器學習的數學基礎專輯
擷取本站知識星球優惠券，複制連結直接打開：
https://t.zsxq.com/y7uvZF6
本站qq群704220115。

加入微信群請掃碼：