29.CF1149C [Tree Generator™](httpswww.luogu.com.cnproblemCF1149C) 區間合并線段樹

29.CF1149C Tree Generator™ 區間合并線段樹

個人Limitの線段樹題單題解主目錄

給定一棵樹的括号序列，要求支援單點修改、查詢樹直徑

考慮區間合并線段樹，每個子樹的括号序列是按照先序周遊進行的，是以考慮合并兩個區間的括号序列時的情況

若從序列中任取一段連續子序列，從中去掉所有比對括号後，剩下的括号組成的路徑一定為一條鍊，鍊長為剩下的子序列

樹上直徑長度即為任意區間去掉比對括号後的長度的最大值。

最長去比對區間 = 最大的（将區間分成兩段）後面的權值和 - 前面的權值和

洛谷傳送門：​​Tree Generator™​​

CF傳送門：​​C. Tree Generator™ (codeforces.com)​​

題目分析

給定一棵樹的括号序列，要求支援單點修改、查詢樹直徑。

區間合并線段樹，隻是要合并的資訊有點多。

如上圖所示，是一顆樹，其直徑由紅線構成，其括号序列為。可以發現即為遞歸搜尋為回溯。我們可以發現：

若從序列中任取一段連續子序列，從中去掉所有比對括号後，剩下的括号組成的路徑一定為一條鍊，鍊長為剩下的子序列長。

那麼不難想到樹上兩點間最長的簡單路徑就是所有區間中去比對括号長度的最大值，例如上面就可以是。長度為

我們不難發現，由于已經比對的括号帶有回溯步驟，對最終答案沒有貢獻。是以最終直徑的序列一定是下列三種之一：

不難發現，前兩種都是第三種的極端情況，我們設反轉的位置叫序列中點，那麼第一種中點在頭部，第二種中點在尾部。

那麼按照括号序列的經典處理套路，我們令, ，那麼我們可以得到最長去比對區間的計算方法：我們可以将這種序清單達為連續左括号(一堆1)連續右括号(一堆-1)，也就是最大的後半段權值和-前半段權值和。

那麼我們考慮如何維護這個東西，發現類似區間最大子段和，很有區間合并線段樹的感覺。那麼就考慮如何用區間合并線段樹解決。

我們首先需要維護區間和：

res.val = a.val + b.val;      

接下來可以維護最大子段和，也就是左右連續選取最大值、無限制連續選取最大值，這個是很經典的套路：

分别讨論跨區間取值即可：

res.lmax = max(a.lmax, b.lmax + a.val), res.lmin = min(a.lmin, b.lmin + a.val);
res.rmax = max(b.lmax, a.rmax + b.val), res.rmin = min(b.rmin, a.rmin + b.val);      

維護完了最大子段和，我們需要維護左右起連續選取最大的權值和(去比對權值和)內插補點：

考慮序列中點(見前文描述)跨區間問題，以下為左起選取序列的情況，我們分别枚舉序列中點在左右時的情況

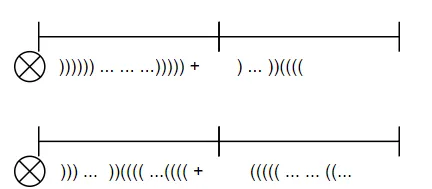
右起的選取與左側類似，那麼我們可以得到合并左右區間的序列選取

res.lcmax = max({a.lcmax, b.lcmax - a.val, a.amax + b.lmax});
res.rcmax = max({b.rcmax, a.rcmax + b.val, b.amax - a.rmin});      

接下來就可以維護選取整個區間下的去比對最大值，這與上面的選取方式是相同的：

res.amax = max(a.amax + b.val, b.amax - a.val);      

有了上面的值，我們就可以計算合并後的無限制去比對最大內插補點，這仍采用枚舉中心點的方式合并計算：

res.ans = max({a.ans, b.ans, b.lcmax - a.rmin, a.rcmax + b.lmax});      

Code

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;

const int N = 2e5 + 10;

string str;

namespace SegTree{
    #define ls rt << 1
    #define rs rt << 1 | 1
    #define lson ls, l,
    #define rson rs, mid + 1,

    struct Info{
        int lmax, lmin, rmax, rmin, lcmax, rcmax, amax, ans, val;
        Info () {}
        void update_leaf(){
            lmax = rmax = max(val, 0ll);
            lmin = rmin = min(val, 0ll);
            lcmax = rcmax = amax = ans = 1;
        }
    } tree[N << 2];

    Info operator+ (Info a, Info b){
        Info res;
        res.val = a.val + b.val;
        res.lmax = max(a.lmax, b.lmax + a.val), res.lmin = min(a.lmin, b.lmin + a.val);
        res.rmax = max(b.lmax, a.rmax + b.val), res.rmin = min(b.rmin, a.rmin + b.val);
        res.lcmax = max({a.lcmax, b.lcmax - a.val, a.amax + b.lmax});
        res.rcmax = max({b.rcmax, a.rcmax + b.val, b.amax - a.rmin});
        res.amax = max(a.amax + b.val, b.amax - a.val);
        res.ans = max({a.ans, b.ans, b.lcmax - a.rmin, a.rcmax + b.lmax});
        return res;
    }

    inline void push_up(int rt){ tree[rt] = tree[ls] + tree[rs]; }

    void build(int rt, int l, int r){
        if(l == r){
            if(str[l] == '(') tree[rt].val = 1;
            if(str[l] == ')') tree[rt].val = -1;
            tree[rt].update_leaf();
            return;
        }
        int mid = l + r >> 1;
        build(lson), build(rson);
        push_up(rt);
    }

    void update(int rt, int l, int r, int pos){
        if(l == r){
            tree[rt].val = (str[l] == '(' ? 1 : -1);
            tree[rt].update_leaf();
            return;
        };
        int mid = l + r >> 1;
        if(mid >= pos) update(lson, pos);
        if(mid < pos) update(rson, pos);
        push_up(rt);
    }

    Info query(){ return tree[1]; }
}

#define SEGRG 1, 1,

inline void solve(){
    int n = 0, m = 0; cin >> n >> m, n = (n - 1) << 1;
    cin >> str, str = '@' + str;
    SegTree::build(SEGRG);
    cout << SegTree::query().ans << endl;
    while(m--){
        int l = 0, r = 0; cin >> l >> r;
        if(str[l] != str[r]){
            swap(str[l], str[r]);
            SegTree::update(SEGRG, l);
            SegTree::update(SEGRG, r);
        }
        cout << SegTree::query().ans << endl;
    }
}

signed main(){
    ios_base::sync_with_stdio(false), cin.tie(0);
    solve();
    return 0;
}