378. 有序矩陣中第 K 小的元素

給你一個

n x n

矩陣

matrix

，其中每行和每列元素均按升序排序，找到矩陣中第

k

小的元素。

請注意，它是 排序後 的第

k

小元素，而不是第

k

個 不同 的元素。

輸入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
輸出：13
解釋：矩陣中的元素為 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13
           

最小堆

由題目給出的性質可知，這個矩陣的每一行均為一個有序數組。問題即轉化為從這 n n n 個有序數組中找第 k k k​ 大的數.

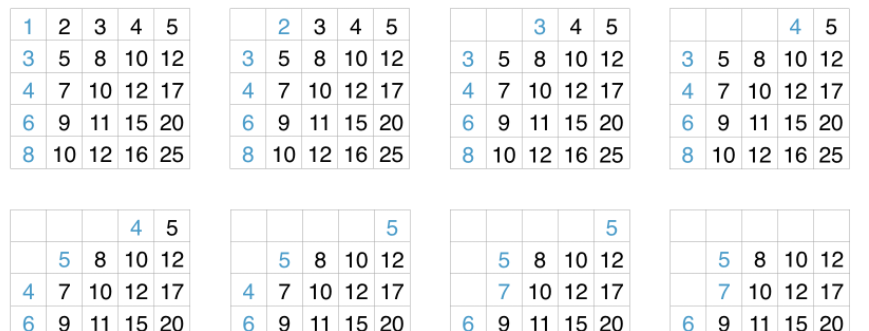
首先把第一列構造最小堆，然後依次删除堆中最小值

num

，并加入矩陣剩餘的最小值。剩餘的最小值是

num

右移一格的值，最小堆（藍色的值）的變換如下：

class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        n = len(matrix) #注：題目中這個矩陣是n*n的，是以長寬都是n

        col = [(matrix[i][0], i ,0) for i in range(n)] #取出第一列的值
        # matrix[i][0]是具體的值，後面的(i,0)是在記錄矩陣中的位置，友善每次右移添加下一個
        heapq.heapify(col) #變成一個heap
        for i in range(k - 1): #一共彈k次：這裡k-1次，return的時候1次
            num, x, y = heapq.heappop(col) #彈出堆裡最小一個
            if y != n - 1: #如果這一行還沒被彈完
                heapq.heappush(col , (matrix[x][y+1], x ,y+1 )) #加入num右邊的一個值
        return heapq.heappop(col)[0]


           

二分法

1. 找出二維矩陣中最小的數 l e f t l e f t left​, 最大的數 right, 那麼第 k k k​ 小的數必定在 left ∼ \sim ∼​ right 之間.
2. mid = ( =( =(​​ left + + +​​ right ) / / 2 ) // 2 )//2​​; 在二維矩陣中尋找小于等于 m i d m i d mid​​ 的元素個數 count.
3. 若這個 count 小于 k k k, 表明第 k k k 小的數在右半部分且不包含 mid ⁡ \operatorname{mid} mid, 即 l e f t = m i d + 1 , r i g h t = l e f t=m i d+1, r i g h t= left=mid+1,right= right, 保證了第 k k k 小的數在 l e f t ∼ r i g h t l e f t \sim right left∼right 之間
4. 若這個 count >= k k k, 表明第 k k k 小的數在左半部分且可能包含 mid, 即 l e f t = l e f t , r i g h t = l e f t=l e f t, r i g h t= left=left,right= mid ⁡ \operatorname{mid} mid, 又保證了第 k k k 小的數在 l e f t ∼ r i g h t l e f t \sim right left∼right之間
5. 因為每次循環中都保證了第 k k k 小的數在 l e f t ∼ r i g h t l e f t \sim right left∼right之間，當 l e f t = = r i g h t l e f t==r i g h t left==right 時，第 k k k 小的數 即被找出，等于 r i g h t \mathrm{right} right

注意：這裡的 l e f t 、 m i d 、 r i g h t left 、mid 、right left、mid、right 是數值，不是索引位置。

count 的計算如下，取 m i d = 8 mid =8 mid=8.

可以這樣描述走法：

• 初始位置在 m a t r i x [ n − 1 ] [ 0 ] matrix[n - 1][0] matrix[n−1][0]​（即左下角）；
• 設目前位置為 matrix ⁡ [ i ] [ j ] \operatorname{matrix}[i][j] matrix[i][j] 。若 matrix ⁡ [ i ] [ j ] ≤ m i d \operatorname{matrix}[i][j] \leq m i d matrix[i][j]≤mid, 則将目前所在列的不大于 m i d m i d mid 的數的數量 (即 i + 1 i+1 i+1 ) 累加到

  count

  中 , 并向右移動, 否則向上移動;
• 不斷移動直到走出格子為止。

class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        row = len(matrix)
        col = len(matrix[0])
        left = matrix[0][0]
        right = matrix[row - 1][col - 1]
        while left < right:
            #每次循環都保證第K小的數在left~right之間，當left==right，第k小的數就是left
            mid = left+(right-left)//2
            count = self.findNotBiggerThanMid(matrix, mid, row, col)
            if count<k:
                #第k小的數在右半部分，且不包含mid
                left = mid + 1
            else :
                #第k小的數在左半部分，可能包含mid
                right = mid
        return right

    def findNotBiggerThanMid(self,matrix,mid,row,col):
        #以列為機關找，找到每一列最後一個<=mid的數即知道每一列有多少個數<=mid
        i, j = row - 1, 0
        count =0
        while i >= 0 and j < col:
            if matrix[i][j] <= mid:
                count += i + 1
                j += 1
            else:
                i -= 1
        return count
           

參考

Krahets - 力扣（LeetCode） (leetcode-cn.com)