主要學習了這位大佬的文章,講的也很通俗易懂了
以下的示例以及一些圖檔也是從大佬那邊抄過來的,主要記錄一下自己的學習感受.
灰色關聯度分析,聽名字很高大上,實際上就是算關聯度的一個方法.就是想看看某幾個因素中,哪個因素對事情的影響更大.比如
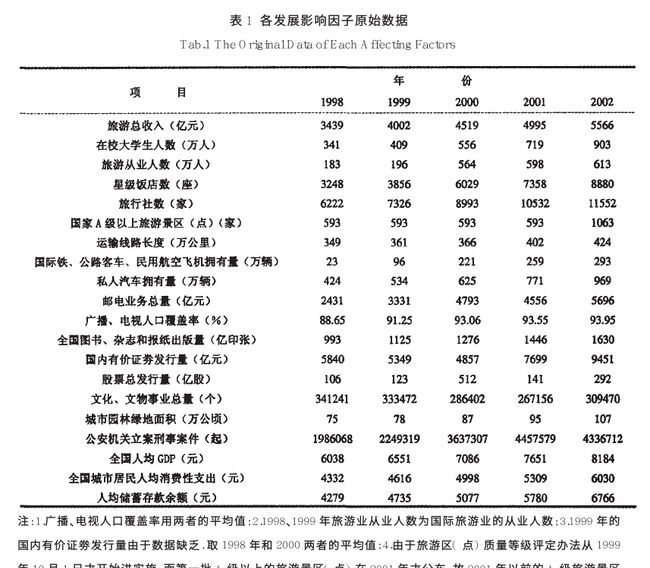
這個例子就算想看,其他這麼一堆因子中,對旅遊總收入的影響,哪個更大一些.個人從結果上看,還挺像熵權法的…
現在知道了就是想算影響關系,那就完成了第一步,确定子母序列,母是結果,子是影響因子.
然後第二步,就要對資料進行預處理了.就想熵權法要歸一化,這個也要…看大神的說法,一般在這裡是用均值化和初值化
初值化 就是每個因素都除以因素中,第一個因子的值就好了.比如在校大學生人數就是每個都除以341
均值化就是每個因素都除以因素的平均值
都挺好了解的,實際上,如果用标準化,或者歸一化,會有不同的排序情況…至于為啥選初值化和均值化,不懂…
資料與處理完後,ok,對着公式操作就好.
先看rho等于0的情況
分子(就是min min那個)就是每一列(列指上面的資料圖的列)第一行的數字(代表了結果)分别減下面每行(代表了影響因子)的絕對值得到一個值,然後再周遊每一列,得到這麼多個值中的最小值.是以對于固定的資料來說,這個值是固定的.
大神部落格中提到,初值化的話,這個分子一定是0,也很好了解,初值化都是除以第一列的值,那第一列都是1,是以1-1=0,0肯定是最小值了
分母就是第i行k列的值的具體值,結果減去影響因子的絕對值.幾何意義上說,就是影響因子和結果的距離,距離越遠,相關度就越低.
再考慮rho,這裡就直接不想多了,rho一般取0.5然後加上去以後可以防止分子為0的情況.别的就不多研究了…max max 跟min min那個算式,前面求的是最大值,這裡求的是最小值.
這樣就能得到一個關聯度矩陣,每個因子關聯矩陣裡對應位置的平均值,就是這個因子的關聯度.
下附代碼
這是可以直接複制使用的代碼
import numpy as np
mom_ = [3439,4002,4519,4995,5566]
son_ = [[341,409,556,719,903],[183,196,564,598,613],[3248,3856,6029,7358,8880]]
mom_ = np.array(mom_)
son_ = np.array(son_)
son_ = son_.T / son_.mean(axis=1)
mom_ = mom_/mom_.mean()
for i in range(son_.shape[1]):
son_[:,i] = abs(son_[:,i]-mom_.T)
Mmin = son_.min()
Mmax = son_.max()
cors = (Mmin + 0.5*Mmax)/(son_+0.5*Mmax)
Mmean = cors.mean(axis = 0)
print(Mmean)
jupyter的運作過程展示,友善了解