Tarjan算法求割點與割邊(python3實作)

from typing import List, Tuple


'''
Trajan算法求無向圖的橋
'''

class Tarjan:
    # 求無向連通圖的橋
    @staticmethod
    def getCuttingPointAndCuttingEdge(edges: List[Tuple]):
        link, dfn, low = {}, {}, {}# link為字典鄰接表
        global_time = [0]
        for a, b in edges:
            if a not in link:
                link[a] = []
            if b not in link:
                link[b] = []
            link[a].append(b)#無向圖
            link[b].append(a)#無向圖
            dfn[a], dfn[b] = 0x7fffffff, 0x7fffffff
            low[a], low[b] = 0x7fffffff, 0x7fffffff


        cutting_points, cutting_edges = [], []

        def dfs(cur, prev, root):
            global_time[0] += 1
            dfn[cur], low[cur] = global_time[0], global_time[0]

            children_cnt = 0
            flag = False
            for next in link[cur]:
                if next != prev:
                    if dfn[next] == 0x7fffffff:
                        children_cnt += 1
                        dfs(next, cur, root)

                        if cur != root and low[next] >= dfn[cur]:
                            flag = True
                        low[cur] = min(low[cur], low[next])

                        if low[next] > dfn[cur]:
                            cutting_edges.append([cur, next] if cur < next else [next, cur])
                    else:
                        low[cur] = min(low[cur], dfn[next])

            if flag or (cur == root and children_cnt >= 2):
                cutting_points.append(cur)

        dfs(edges[0][0], None, edges[0][0])
        return cutting_points, cutting_edges


class Solution:
    def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:
        edges = [(a, b) for a, b in connections]
        cutting_dots, cutting_edges = Tarjan.getCuttingPointAndCuttingEdge(edges)
        return [[a, b] for a, b in cutting_edges]


connections = [[0,1],[1,2],[2,0],[1,3]]
n = 4
s = Solution()
result = s.criticalConnections(n,connections)
print(result)      

​​1192. 查找叢集内的「關鍵連接配接」​​

難度困難39

力扣資料中心有 ​

​n​

​​ 台伺服器，分别按從 ​

​0​

​​ 到 ​

​n-1​

​ 的方式進行了編号。

它們之間以「伺服器到伺服器」點對點的形式互相連接配接組成了一個内部叢集，其中連接配接 ​

​connections​

​ 是無向的。

從形式上講，​

​connections[i] = [a, b]​

​​ 表示伺服器 ​

​a​

​​ 和 ​

​b​

​ 之間形成連接配接。任何伺服器都可以直接或者間接地通過網絡到達任何其他伺服器。

「關鍵連接配接」是在該叢集中的重要連接配接，也就是說，假如我們将它移除，便會導緻某些伺服器無法通路其他伺服器。

請你以任意順序傳回該叢集内的所有 「關鍵連接配接」。

示例 1：

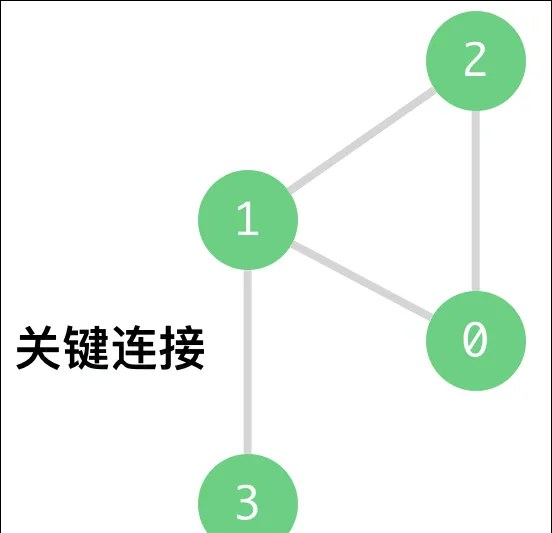
輸入：n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]

輸出：[[1,3]]

解釋：[[3,1]] 也是正确的。

• ​

  ​1 <= n <= 10^5​

  ​
• ​

  ​n-1 <= connections.length <= 10^5​

  ​
• ​

  ​connections[i][0] != connections[i][1]​

  ​
• 不存在重複的連接配接