【高等數學】曲線積分和曲面積分

本文已參與「新人創作禮」活動，一起開啟掘金創作之路。

對弧長的曲線積分

一、對弧長的曲線積分的定義

設$L$為$xOy$面内的一條光滑曲線弧，函數$f(x,y)$在$L$上有界，在$L$上任意插入一點列$M_1,M_2,\cdots,M_n-1$，把$L$分成$n$個小段，設第$i$個小段的長度為$\Delta s_i$，又$(\xi_i,\eta_i)$為第$i$個小段上任意取定的一點，作乘積$f(\xi_i,\eta_i)\Delta s_i\quad(i=1,2,\cdots,n)$，并作和$\sum^n_{i=1}f(\xi_i,\eta_i)\Delta s_i$，如果當各校弧段的長度的最大值$\lambda\to0$時，這和的極限總存在，且與曲線弧$L$的分發及點$(\xi_i,\eta_i)$的取法無關，那麼稱此極限為函數$f(x,y)$在曲線弧$L$上對弧長的曲線積分或第一類曲線積分，記作$\int_Lf(x,y)ds$，即$\int_Lf(x,y)ds=\lim_{\lambda\to1}\sum^n_{i=1}f(\xi_i,\eta_i)\Delta s_i$，其中$f(x,y)$叫做被積函數，$L$叫做積分弧段

二、對弧長的曲線積分的幾何意義

曲線弧的品質

三、對弧長的曲線積分的性質

性質1（線性）：若$\alpha,\beta$為常數，則$\int_L[\alpha f(x,y)+\beta g(x,y)]ds=\alpha\int_Lf(x,y)ds+\beta\int_Lg(x,y)ds$

性質2（曲線可加）：若積分弧段$L$可分為兩段光滑曲線弧$L_1$和$L_2$，則$$\int_Lf(x,y)ds=\int_{L_1}f(x,y)ds+\int_{L_2}f(x,y)ds$$

性質3：設在$L$上$f(x,y)\leq g(x,y)$，則$\int_Lf(x,y)ds\leq\int_Lg(x,y)ds$。特别地，有$|\int_Lf(x,y)ds|\leq\int_L|f(x,y)|ds$

四、對弧長的曲線積分的計算方法

1. 參數方程

$L:\begin{cases}x=x(t)\y=y(t)\end{cases},\alpha\leq t\leq \beta$

則$\int_Lf(x,y)ds=\int^\beta_\alpha f(x(t),y(t))\sqrt{x'^2(t)+y'^2(t)}dt$

推導

$d^2x+d^2y=d^2s$

$ds=\sqrt{d^2x+d^2y}=\sqrt{1+(\frac{dy}{dx})^2}dx$

2. 直角坐标

$L:y=y(x),a\leq x\leq b$

則$\int_Lf(x,y)ds=\int^b_af(x,y(x))\sqrt{1+y'^2(x)}dx$

推導

$d^2x+d^2y=d^2s$

$ds=\sqrt{d^2x+d^2y}=\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt$

3. 極坐标

$L:r=r(\theta),\alpha\leq\theta\leq\beta$

則$\int_Lf(x,y)ds=\int^\beta_\alpha f(r(\theta)\cos\theta,r(\theta)\sin\theta)\sqrt{r^2(\theta)+r'^2(\theta)}d\theta$

推導

$d^2x+d^2y=d^2s$

$\begin{cases}x=r\cos\theta\y=r\sin\theta\end{cases}$

$ds=\sqrt{x'(\theta)^2+y'(\theta)^2}dt=\sqrt{[(r\cos\theta)']^2+[(r\sin\theta)']^2}d\theta$

例1：計算$\int_Le^{\sqrt{x^2+y^2}}ds$其中$L$為圓周$x^2+y^2=a^2$，直線$y=x$及$x$軸在第一象限内所圍成的扇形整個邊界

ax=plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))

ax.spines['left'].set_position(('data',0))

ax.set_aspect(1)

X=np.linspace(-1,1,50)

a=1

f1=lambda x:(a**2-x**2)**0.5

f2=lambda x:(a**2-x**2)**0.5

f3=lambda x:x

f4=lambda x:0

s1=pd.Series(f1(X),index=X)

s2=pd.Series(f2(X),index=X)

s3=pd.Series(f3(X),index=X)

s4=pd.Series(f4(X),index=X)

s1.plot()

s2.plot()

s3.plot(color='orange')

s4.plot(color='red')

plt.xlim(0,1)

plt.ylim(0,1)

plt.xticks([1])

plt.yticks([0,1])

ax.set_xticklabels(['a'])

ax.set_yticklabels([0,'a'])

ax.annotate('A',(1,0))

ax.annotate('B',(2**0.5/2,2**0.5/2))

           

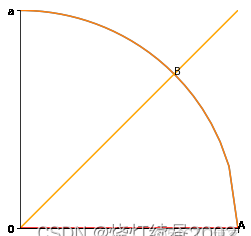
$L_{OA}:y=0\quad(0\leq x\leq a)$

$L_{OB}:y=x\quad(0\leq x\leq \frac{\sqrt2}2a)$

$L_{AB}:\begin{cases}x=a\cos t\y=a\sin t\end{cases}\quad(0\leq t\leq \frac\pi4)$

$\int_{L_{OA}}=\int^a_0e^x\sqrt{1+0^2}dx$

$\int_{L_{OB}}=\int^{\frac{\sqrt2}2a}_0e^{\sqrt2x}\sqrt{1+1^2}dx$

$\int_{L_{AB}}=\int^{\frac\pi4}_0e^a\sqrt{(a\cos t)'^2+(a\sin t)'^2}dt=\int^{\frac\pi4}_0e^aadt$

$\int_L=e^a(2+\frac\pi4a)-2$

例2：計算曲線積分$\int_\Gamma(x^2+y^2+z^2)ds$，其中$\Gamma$為螺旋線$x=a\cos t,y=a\sin t,z=kt$上相應于$t$從$0$到$2\pi$上的一段弧

plt.rcParams['figure.figsize']=(8,8)

ax=plt.gca(projection="3d")

T=np.linspace(-10,10,200)

a=1

k=2

X=lambda t:a*np.cos(t)

Y=lambda t:a*np.sin(t)

Z=lambda t:k*t

ax.plot(X(T),Y(T),Z(T))

           

（這裡畫圖沒啥用，消磨一下垃圾時間）

$\begin{aligned}\int_\Gamma(x^2+y^2+z^2)ds&=\int^{2\pi}_0[(a\cos t)^2+(a\sin t)^2+(kt)^2]\cdot\sqrt{(-a\sin t)^2+(a\cos t)^2+k^2}dt\&=\sqrt{a^2+k^2}(a^2t+\frac{k^2}3t^3)\Big|^{2\pi}_0\&=\frac23\pi\sqrt{a^2+k^2}(3a^2+4pi^2k^2)\end{aligned}$

對坐标的曲線積分

一、對坐标的曲線積分的定義

設$L$為$xOy$面内從點$A$到點$B$的一條有向光滑曲線弧，函數$P(x,y)$與$Q(x,y)$在$L$上有界，在$L$上沿$L$的方向任意插入一點$M_1(x_1,y_1),M_2(x_2,y_2),\cdots,M_{n-1}(x_{n-1},y_{n-1})$，把$L$分成$n$個有向小弧段$M_{i-1}M_i\quad(i=1,2,\cdots,n;M_0=A,M_n=B)$，設$\Delta x_i=x_i-x_{i-1},\Delta y_i=y_i-y_{i-1}$，點$(\xi_i,\eta_i)$為$M_{i-1}M_i$上任意取定的點，作乘積$P(\xi_i,\eta_i)\Delta x_i\quad(i=1,2,\cdots,n)$，并作和$\sum_{i=1}^nP(\xi_i,\eta_i)\Delta_i$，如果當各校弧段程度的最大值$\lambda\to0$時，這和的極限總存在，且與曲線弧$L$的分發及點$(\xi_i,\eta_i)$的取法無關，那麼稱此極限為函數$P(x,y)$在有向線弧$L$上對坐标$x$的曲線積分，記作$\int_LP(x,y)dx$；類似地，如果$\lim_{\lambda\to0}\sum^n_{i=1}Q(\xi_i,\eta_i)\Delta y_i$總存在，且與曲線弧$L$的分發及點$(\xi_i,\eta_i)$的取法無關，那麼稱此極限為函數$Q(x,y)$在有向線弧$L$上對坐标$y$的曲線積分，記作$\int_LQ(x,y)dy$，即$\int_LP(x,y)dx=\lim_{\lambda\to0}\sum^n_{i=1}P(\xi_i,\eta_i)\Delta x_i,\int_LQ(x,y)dy=\lim_{\lambda\to0}\sum^n_{i=1}Q(\xi_i,\eta_i)\Delta y_i$，其中$P(x,y),Q(x,y)$叫做被積函數，$L$叫做積分弧，以上兩個積分叫做對坐标的曲線積分，也叫作第二類曲線積分

二、對坐标的曲線積分的幾何意義

變力沿曲線所作的功

三、對坐标的曲線積分的性質

性質1（線性）：設$\alpha$與$\beta$為常數，則$\int_L\alpha[P_1(x,y)dx+Q_1(x,y)dy]+\beta[P_2(x,y)dx+Q_2(x,y)dy]=\alpha\int_LP_1(x,y)dx+Q_1(x,y)dy+\beta\int_LP_2(x,y)dx+Q_2(x,y)dy$

性質2（曲線可加）：若有向曲線弧$L$可分為兩段光滑的有向曲線弧$L_1$和$L_2$，則$\int_LP(x,y)dx+Q(x,y)dy=\int_{L_1}P(x,y)dx+Q(x,y)dy+\int_{L_2}P(x,y)dx+Q(x,y)dy$

性質3（方向性）：設$L$是有向光滑曲線弧，$L^-$是$L$的反向曲線弧，則$\int_LP(x,y)dx+Q(x,y)dy=-\int_LP(x,y)dx+Q(x,y)dy$

做計算時一定要注意方向性，是從哪一點到哪一點，決定積分的上下限

例1：計算$\int_L2xydx+x^2dy$，其中$L$為抛物線$y=x^2$上從點$O(0,0)$到點$B(1,1)$的一段弧

$\begin{aligned}\int_L2xydx+x^2dy&=\int^1_02x\cdot(x^2)dx+x^2\cdot y'(x)dx\&\text{此處把}y\text{看做因變量，}x\text{看做自變量，是以有}dy=y'(x)dx\&=\int^1_0(2x^3+2x^3)dx\&=1\end{aligned}$

如果題目中出現$y^2=x$，可以把$x$看做因變量，$y$看做自變量，有$dx=x'(y)dy$

例2：計算$\int_Ly^2dx$，其中$L$的半徑為$a$，圓心在原點，從$A(a,0)$到$B(-a,0)$的按逆時針方向繞行的上半圓周

令$\begin{cases}x=a\cos\theta\y=a\sin\theta\end{cases}\quad\theta:0\to\pi$

$\begin{aligned}\int_Ly^2dx&=\int^\pi_0(a\sin\theta)^2(-a\sin\theta)d\theta\&=-a^3\int^\pi_0\sin^3\theta d\theta\&=-2a^3\int^\frac\pi2_0\sin^3\theta d\theta\&=-2a^3\frac23\&=-\frac43a^3\end{aligned}$

可以換成極坐标做，極坐标的$\rho$沒有方向

例3：計算$\int_L2xydx+x^2dy$，其中$L$為有向折線$OAB$，這裡$O,A,B$分别為$(0,0),(1,0),(1,1)$

$OA:y=0,x:0\to1$

$AB:x=1,y:0\to1$

$\begin{aligned}\int_L2xydx+x^2dy&=\int_{L_{OA}}2xydx+x^2dy+\int_{L_{AB}}2xydx+x^2dy\&=0+\int^1_01^2dy\&=1\end{aligned}$

對于$OA$，因為$y=0$，是以$2xydx=0$、$dy=0$，即$x^2dy=0$，是以$\int_{L_{OA}}2xydx+x^2dy=0$

對于$AB$，因為$x=1$，是以$dx=0$，即$2xydx=0$，是以$\int_{L_{AB}}2xydx+x^2dy=\int^1_01^2dy$

格林公式及其應用

一、格林公式

1. 定義

設閉區域$D$由分段光滑的曲線$L$圍成，若函數$P(x,y)$及$Q(x,y)$在$D$上具有一階連續偏導數，則有$$\int_LPdx+Qdy=\iint\limits_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy$$，其中$L$是$D$的取正向的邊界曲線，即為格林公式

證明：

先證$-\int\limits_D\frac{\partial P}{\partial y}dxdy=\oint_LPdx$

假定區域$D$的形狀如下（用平行于$y$軸的直線穿過區域，與區域邊界曲線的交點至多兩點）

易見，圖二所表示區域是圖一所表示區域的一種特殊情況，僅對圖一所表示區域$D$給予證明

$D:\begin{cases}a\leq x\leq b\\phi_1(x)\leq y\leq\phi_2(x)\end{cases}$

$\begin{aligned}-\int\limits_D\frac{\partial P}{\partial y}dxdy&=-\int^b_adx\int^{\phi_2(x)}{\phi_1(x)}\frac{\partial P}{\partial y}dy\&=-\int^b_a[P(x,y)]^{\phi_2(x)}{\phi_1(x)}dx\&=-\int^b_a{P[x,\phi_2(x)]-P[x,\phi_1(x)]}dx\end{aligned}$

$\begin{aligned}\int_LPdx&=\int_{\widehat{AB}}Pdx+\int_{\overline{BC}}Pdx+\int_{\widehat{CE}}Pdx++\int_{\overline{EA}}Pdx\&=\int^b_aP[x,\phi_1()]dx+0+\int^a_bP[x,\phi_2(x)]+0\end{aligned}$

是以$-\int\limits_D\frac{\partial P}{\partial y}dxdy=\oint_LPdx$

同理$-\int\limits_D\frac{\partial Q}{\partial x}dxdy=\oint_LQdy$

兩式合并後即得格林公式$\int_LPdx+Qdy=\iint\limits_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy$

單連通區域：設$D$為平面區域，如果$D$内任一閉曲線所圍的部分區域都屬于$D$，則$D$稱為平面單連通區域。直覺地說，單連通區域是沒有空間的區域，否則稱為複連通區域。

曲線關于區域的正方向：當$xOy$平面上的曲線起點與終點重合時，則稱曲線為閉曲線。設平面的閉曲線$L$圍成平面區域$D$，并規定當一個人沿閉曲線$L$環行時，區域$D$總是位于此人的左側，稱此人行走方向為曲線$L$關于區域$D$的正方向，反之為負方向。

複連通區域下格林公式$$\iint\limits_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint_L(Pdx+Qdy)-\oint_l(Pdx+Qdy)$$

切割成兩個單連通區域，然後對兩個單連通區域分别使用格林公式。

$\begin{aligned}\iint\limits_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy&=\iint\limits_{D_1}(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy+\iint\limits_{D-2}(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy\&=\oint_{C_1+C_2}Pdx+Qdy\end{aligned}$

因為紅色部分抵消。加入隻剩下内部的順時針線$l$和外部的逆時針線$L$。

證畢

作者：oneslide

連結：https://blog.csdn.net/qq_33745102/article/details/111877109

部分有修改

例1：計算曲線積分$\oint_L(x^2+y)dx-(x+\sin^2y)dy$，其中$L$是在圓周$y=\sqrt{2x-x^2}$上由點$(0,0)$到點$(1,1)$的一段弧

ax=plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))

ax.spines['left'].set_position(('data',0))

ax.set_aspect(1)

X=np.linspace(0,2,50)

f=lambda x:(2*x-x**2)**0.5

s1=pd.Series(f(X),index=X)

s1.plot()

           

（高中知識告訴我這是個半圓）

設$L_1:x=1,y:1\to0;L_2:y=0,x:1\to0$

$\int_L=\int_{L+L_1+L_2}-\int_{L_1}-\int_{L_2}$

$\int_{L+L_1+L_2}=-\iint\limits_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})d\sigma=0$

$\int_{L_1}=\int^0_1[-(1+\sin^2y)]dy=\frac32-\frac14\sin2$

$\int_{L_2}=\int^0_1x^2dx=-\frac13$

$\int_L=0-(\frac32-\frac14\sin2)-(-\frac13)=-\frac76+\frac14\sin2$

二、平面上曲線積分與路徑無關

1. 定義

設$G$是一個區域，$P(x,y)$以及$Q(x,y)$在區域$G$内具有一階連續偏導數，如果對于$G$内任意指定的兩個點$A,B$以及$G$内從點$A$到點$B$的任意兩條曲線$L_1,L_2$，等式$\int_{L_1}Pdx+Qdy=\int_{L_2}Pdx+Qdy$恒成立，就說曲線積分$\int_LPdx+Qdy$在$G$内與路徑無關，否則便說與路徑有關

2. 充要條件

設區域$G$是一個單連通域，若函數$P(x,y)$與$Q(x,y)$在$G$内有一階連續偏導數，則曲線積分$\int_LPdx+Qdy$在$G$内與路徑無關（或沿$G$内任意閉曲線的曲線積分為零）的充分必要條件是$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$在$G$内恒成立

例1：計算曲線積分$\oint_L(x^2+y)dx-(x+\sin^2y)dy$，其中$L$是在圓周$y=\sqrt{2x-x^2}$上由點$(0,0)$到點$(1,1)$的一段弧

$P=x^2-y$

$Q=-(x+\sin^2y)$

$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}=-1$

故$\int_L$與路徑無關

$L_1:y=0,x:0\to1;L_2:x=1,y:0\to1$

$\int_L=\int_{L_1}+\int_{L_2}$

$\int_{L_1}=\int^1_0x^2dx=\frac13$

$\int_{L_2}=\int^1_0-(1+\sin^2y)dy=-\frac32+\frac14\sin2$

$\therefore\int_L=\int_{L_1}+\int_{L_2}=-\frac76+\frac14\sin2$

三、二進制函數的全微分求積

定理1

設區域$G$是一個單連通域，若函數$P(x,y)$與$Q(x,y)$在$G$内具有一階連續偏導數，則$P(x,y)dx+Q(x,y)dy$在$G$内為某一函數$u(x,y)$的全微分的充分必要條件是$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$在$G$内恒成立

推論：設區域$G$是一個單連通域，若函數$P(x,y)$與$Q(x,y)$在$G$内具有一階連續偏導數，則曲線積分$\int_LPdx+Qdy$在$G$内與路徑無關的充分必要條件是（等價于$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$在$G$内恒成立），在$G$記憶體在函數$u(x,y)$，使$du=Pdx+Qdy$

全微分方程的定義

一個微分方程寫成$P(x,y)dx+Q(x,y)dy=0$的形式後，如果等式的左端恰好是某一個函數$u(x,y)$的全微分（此處是不是某一個函數$u(x,y)$的全微分看上面的定理1），即$du(x,y)=P(x,y)dx+Q(x,y)dy$，那麼就把$P(x,y)dx+Q(x,y)dy=0$叫做全微分方程，且$u(x,y)=\int^{(x,y)}_{(x_0,y_0)}P(x,y)dx+Q(x,y)dy=C$為全微分方程的隐式通解，其中C為任意常數

例2：求解方程$(5x^4+3xy^2-y^3)dx+(3x^2y-3xy^2+y^2)dy=0$

設$A(x,0),B(x,y)$

$\begin{aligned}u(x,y)&=\int^{(x,y)}{(0,0)}(5x^4+3xy^2-y^3)dx+(3x^2y-3xy^2+y^2)dy\&(0,0)\text{隻是取得為了友善計算，取其他點也可以}\&\text{注意此處積分上的}x,y\text{和被積函數中的}x,y\text{不是一個}x,y\&\text{可以寫為}\int^{(x,y)}{(0,0)}(5s^4+3st^2-t^3)ds+(3s^2t-3st^2+t^2)dt\&=\int_{OA}+\int_{AB}\&=\int^x_05x^4dx+\int^y_0(3x^2y-3xy^2+y^2)dy\&=x^5+\frac32x^2y^2-xy^3+\frac13y^3=C\end{aligned}$

故通解為$x^5+\frac32x^2y^2-xy^3+\frac13y^3=C$

對面積的曲面積分

一、對面積的曲面積分的定義

設曲面$\sum$是光滑的，函數$f(x,y,z)$在$\sum$上有界，把$\sum$任意分成n小塊$\Delta  S_i$（$\Delta S_i$同時代表第$i$小塊曲面的面積），設$(\xi_i,\eta_i,\zeta_i)$是$\Delta S_i$上任意取定的一點，做乘積$f(\xi_i,\eta_i,\zeta_i)\Delta S_i\quad(i=1,2,3,\cdots,n)$，并作和$\sum^n_{i=1}f(\xi_i,\eta_i,\zeta_i)\Delta S_i$，如果當各小塊曲面的直徑的最大值$\lambda\to0$時，這和的極限總存在，且與曲面$\sum$的分發及點$(\xi_i,\eta_i,\zeta_i)$的取法無關，那麼稱此極限為函數$f(x,y,z)$在曲面$\sum$上對面積的曲面積分或第一類曲面積分，記作$\iint\limits_{\sum} f(x,y,z)dS$，即$\iint\limits_{\sum} f(x,y,z)dS=\lim_{\lambda\to0}\sum^n_{i=1}f(\xi_i,\eta_i,\zeta_i)\Delta S_i$，其中$f(x,y,z)$叫做被積函數，$\sum$叫做積分曲面

二、對面積的曲面積分的幾何意義

密度不均勻的曲面的品質

三、對面積的曲面積分的性質

性質1（線性）：若$\alpha,\beta$為常數，則$\iint\limits_{\sum}[\alpha f(x,y,z)+\beta g(x,y,z)]dS=\alpha\iint\limits_{\sum} f(x,y,z)dS+\beta\iint\limits_{\sum} g(x,y,z)dS$

性質2（曲面可加）：若積分曲面$\sum$可分為兩個光滑的曲面$\sum_1,\sum_2$，則$\iint\limits_{\sum} f(x,y,z)dS=\iint\limits_{\sum_1}f(x,y,z)dS+\iint\limits_{\sum_2}f(x,y,z)dS$

性質3（比較定理）：設在$\sum$上$f(x,y,z)\leq g(x,y,z)$，則$\iint\limits_{\sum} f(x,y,z)dS\leq\iint\limits_{\sum} g(x,y,z)dS$，特别的，有$\Big|\iint\limits_{\sum} f(x,y,z)dS\Big|\leq\iint\limits_{\sum}|f(x,y,z)|dS$

四、對面積的曲面積分的計算方法

• 設$\sum:z=z(x,y),(x,y)\in D$

      則$\iint\limits_{\sum} f(x,y,z)dS=\iint\limits_D f(x,y,z(x,y))\sqrt{1+z_x^{'2}+z_y^{'2}}d\sigma$

• 設$\sum:y=y(x,z),(x,z)\in D$

      則$\iint\limits_{\sum} f(x,y,z)dS=\iint\limits_D f(x,y(x,z),z)\sqrt{1+y_x^{'2}+y_z^{'2}}d\sigma$

• 設$\sum:x=x(y,z),(y,z)\in D$

      則$\iint\limits_{\sum} f(x,y,z)dS=\iint\limits_D f(x(y,z),y,z)\sqrt{1+x_y^{'2}+x_z^{'2}}d\sigma$

例1：計算$\iint\limits_{\sum} xyzdS$，其中$\sum$是由平面$x=0,y=0,z=0$及$x+y+z=1$所圍成的四面體的整個邊界曲面

設四面體在$xOy$上的面$\sum_2:z=0$，在$xOz$上的面$\sum_1:y=0$，在$yOz$上的面$\sum_3:x=0$，剩下的一個面設在$xOy$的投影為$\sum_4$

$\begin{aligned}\iint\limits_{\sum}&=\iint\limits_{\sum_1}+\iint\limits_{\sum_2}+\iint\limits_{\sum_3}+\iint\limits_{\sum_4}\&=0+0+0+\iint\limits_{\sum_4}xyzdS\&=\iint\limits_{D_{xy}}xy(1-x-y)\sqrt{1+z_x^{'2}+z_y^{'2}}dxdy\&=\sqrt3\int^1_0dx\int^{1-x}_0xy(1-x-y)dy\&=\frac{\sqrt3}{120}\end{aligned}$

對坐标的曲面積分

一、對坐标的曲面積分的定義

設$\sum$為光滑的有向曲面，函數$R(x,y,z)$在$\sum$上有界，把$\sum$任意分成$n$塊小曲面$\Delta S_i$（$\Delta S_i$同時又表示第i塊小曲面的面積），$\Delta S_i$在$xOy$面上的投影為$(\Delta S_i){xy}$，$(\xi_i,\eta_i,\zeta_i)$是$\Delta S_i$上任意取定的一點，作乘積$R(\xi_i,\eta_i,\zeta_i)(\Delta S_i)\quad(i=1,2,3,\cdots,n)$，并作和$\sum^n{i=1}R(\xi_i,\eta_i,\zeta_i)(\Delta S_i){xy}$，如果當各小塊曲面的直徑的最大值$\lambda\to0$時，這和的極限總存在，且與曲面$\sum$的分發及點$(\xi_i,\eta_i,\zeta_i)$的取法，無關，那麼稱此極限為函數$R(x,y,z)$在有向曲面$\sum$對坐标$x,y$的曲面積分，記作$\iint\limits{\sum} R(x,y,z)dxdy$，即$\iint\limits_{\sum} R(x,y,z)dxdy=\lim_{\lambda\to0}\sum^n_{i=1}(\xi_i,\eta_i,\zeta_i)(\Delta S_i)_{xy}$，其中R$(x,y,z)叫$做被積函數，$\sum$叫做積分曲面

類似地可以定義函數$P(x,y,z)$在有向曲面$\sum$上對坐标$y,z$的曲面積分$\iint\limits_{\sum} P(x,y,z)dydz$，即為$\iint\limits_{\sum} P(x,y,z)dydz=\lim_{\lambda\to0}\sum^n_{i=1}P(\xi_i,\eta_i,\zeta_i)(\Delta S_i)_{xy}$；

定義函數$P(x,y,z)$在有向曲面$\sum$上對坐标$z,x$的曲面積分$\iint\limits_{\sum} P(x,y,z)dzdx$，即為$\iint\limits_{\sum} P(x,y,z)dzdx=\lim_{\lambda\to0}\sum^n_{i=1}P(\xi_i,\eta_i,\zeta_i)(\Delta S_i)_{zx}$

二、對坐标的曲面積分的幾何意義

流向曲面一側的流量

三、對坐标的曲面積分的性質

性質1（線性）：設$\alpha$與$\beta$為常數，則$\iint\limits_{\sum}[\alpha(P_1dydz+Q_1dzdx+P_1dxdy)+\beta(P_2dydz+Q_2dzdx+P_2dxdy)]=\alpha\iint\limits_{\sum} P_1dydz+Q_1dzdx+P_1dxdy+\beta\iint\limits_{\sum} P_2dydz+Q_2dzdx+P_2dxdy$

性質2（曲面可加）：若有向曲面$\sum$可分為兩段光滑的有向曲面$\sum_1$和$\sum_2$，則$\iint\limits_{\sum} Pdydz+Qdzdx+Pdxdy=\iint\limits_{\sum_1} Pdydz+Qdzdx+Pdxdy+\iint\limits_{\sum_2} Pdydz+Qdzdx+Pdxdy$

性質3（方向性）：設$\sum$是有向曲面，$\sum^-$表示$\sum$取反側的有向曲面，則$\iint\limits_{\sum^-}P(x,y,z)dydz=-\iint\limits_{\sum}P(x,y,z)dydz$

$\iint\limits_{\sum^-}P(x,y,z)dzdx=-\iint\limits_{\sum}P(x,y,z)dzdx$

$\iint\limits_{\sum^-}P(x,y,z)dxdy=-\iint\limits_{\sum}P(x,y,z)dxdy$

四、對坐标的曲面積分的計算方法

設$\sum:z=z(x,y),(x,y)\in D$，則$\iint\limits_{\sum} R(x,y,z)dxdy=\pm\iint\limits_DR[x,y,z(x,y)]dxdy$

設$\sum:y=y(z,x),(z,x)\in D$，則$\iint\limits_{\sum} R(x,y,z)dzdx=\pm\iint\limits_DR[x,y(z,x),z]dzdx$

設$\sum:x=x(y,z),(y,z)\in D$，則$\iint\limits_{\sum} R(x,y,z)dydz=\pm\iint\limits_DR[x(y,z),y,z]dydz$

正負号由面的法向量與對應軸正方向的夾角決定，銳角取正，鈍角取負

例1：計算曲面積分$\iint\limits_{\sum} xyzdxdy$，其中$\sum$是球面$x^2+y^2+z^2=1$外側，在$x\geq0,y\geq0$的部分

$\sum_1:z=-\sqrt{1-x^2-y^2}$

$\sum_2:z=\sqrt{1-x^2-y^2}$

$\begin{aligned}\iint\limits_{\sum}&=\iint\limits_{\sum_1}+\iint\limits_{\sum_2}\&=-\iint\limits_{D_{xy}}xy[-\sqrt{1-x^2-y^2}]dxdy+\iint\limits_{D_{xy}}xy\sqrt{1-x^2-y^2}dxdy\&=2\iint\limits_{D_{xy}}xy\sqrt{1-x^2-y^2}dxdy\&=2\int^\frac\pi2_0d\theta\int^1_0r^2\sin\theta\cos\theta\sqrt{1-r^2}\cdot rdr\&=\frac2{15}\end{aligned}$

高斯公式與散度、旋度

一、高斯公式的定義

設空間閉區域$\Omega$是由分片光滑的比曲面$\sum$所圍成，若函數$P(x,y,z),Q(x,y,z),R(x,y,z)$在$\Omega$上具有一階連續偏導數，則有$\iint\limits_{\sum} Pdydz+Qdzdx+Rdxdy=\iiint\limits_\Omega(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv$，或$\iint\limits_{\sum}(P\cos\alpha+Q\cos\beta+R\cos\gamma)dS=\iiint\limits_\Omega(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv$

（$\cos\alpha dS=dydz,\cos\beta dS=dzdx,\cos\gamma dS=dxdy$）

對于$\iiint\limits_\Omega(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv$也有正負号，取面外側為正，内側為負

例1：利用高斯公式計算曲面積分$\iint\limits_{\sum}(x-y)dxdy+(y-z)xdydz$，其中$\sum$為柱面$x^2+y^2=1$及平面$z=0,z=3$所圍成的空間閉區域$\Omega$的整個邊界曲面的外側

$\begin{aligned}\iint\limits_{\sum}(x-y)dxdy+(y-z)xdydz&=+\iiint\limits_\Omega[(y-z)+0+0]d\theta\&=\int^{2\pi}_0d\theta\int^1_0rdr\int^3_0(r\sin\theta-z)dz\&=-\frac92\pi\end{aligned}$

二、散度的定義

設有向量場$\boldsymbol A(x,y,z)={P,Q,R}$，其中$P$、$Q$、$R$均具有一階連續偏導數，則$div\boldsymbol A=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}$

例2：求向量場$\boldsymbol A=y^2\boldsymbol i+xy\boldsymbol j+xz\boldsymbol k$的散度

$P=y^2,Q=xy,R=xz$

$div\boldsymbol A=0+x+x=2x$

三、旋度的定義

設有向量場$\boldsymbol A(x,y,z)={P,Q,R}$，其中$P$、$Q$、$R$均具有一階連續偏導數，則$\boldsymbol {rotA}=\left|\begin{matrix}\boldsymbol i&\boldsymbol j&\boldsymbol k\\frac\partial{\partial x}&\frac\partial{\partial y}&\frac\partial{\partial z}\P&Q&R\end{matrix}\right|$