【優化排程】基于改進遺傳算法求解農業水資源排程問題（Matlab代碼實作）

目錄

​​1 概述​​

​​2 運作結果​​

​​3 參考文獻​​

​​4 Matlab代碼實作​​

1 概述

科學的渠系配水決策可以減少渠系輸水過程中的滲水損失和無效棄水,提高灌溉水使用率。國内外學者對渠系優化配水決策方法進行了許多研究，Suryavanshi等(1986)最早在假定上級配水管道是由一組等流量流管組成,流管流量等于下級管道流量的基礎上,以減小管道工程投資為目标,确定上級管道流管數的1992)将其用于渠系優化配水研究中,提出了基于0一線性規劃配水模型及算法["。基于上述思想﹐王智等(l規劃法的下級管道等流量時優化配水模型并編制了計算機程式2。Reddy等(1999) [3'、Anwar等(2001)對文獻[1]、[2]的配水模型進行了改進,加入了各下級管道在使用者預定的配水時間窗内配水的要求,解決了輪期内下級管道配水時間與實際需求配水時間差異而造成的作物減産問題。而呂宏興等(2000)改進了文獻[2]模型的目标函數,提出了各下級管道配水時間均一化處理方法,使上級管道可在同一時間關閉.減少了配水閘門調節次數IS'。駱莉等(2000)、宋松柏等(2004)分别研究了文獻[2]、[5]模型的遺傳算法求解方法,顯著提高了模型的求解速度﹐解決了在下級管道較多時模型求解困難的問題5.1。馬孝義等(2005)以渠系輸水損失最小為目标,提出了以灌水組數最大和最長灌水組配水時問最小的二級目标優化配水模型及遺傳算法求解方法,并在對複雜渠系抽象概化的基礎上﹐研制了一種易于快速搭建、通用性強的渠系配水軟體[3]。但上述研究都是基于流管假定下的改進,隻能解決下級管道流量相等條件下的渠系優化配水編組問題。而在大多數情況下﹐由于地形、作物種植類型的變化等，下級管道設計流量變化較大,現有方法存在明顯缺陷。為此,需進一步研究下級管道流量不等時的渠系優化配水模型及其求解算法。

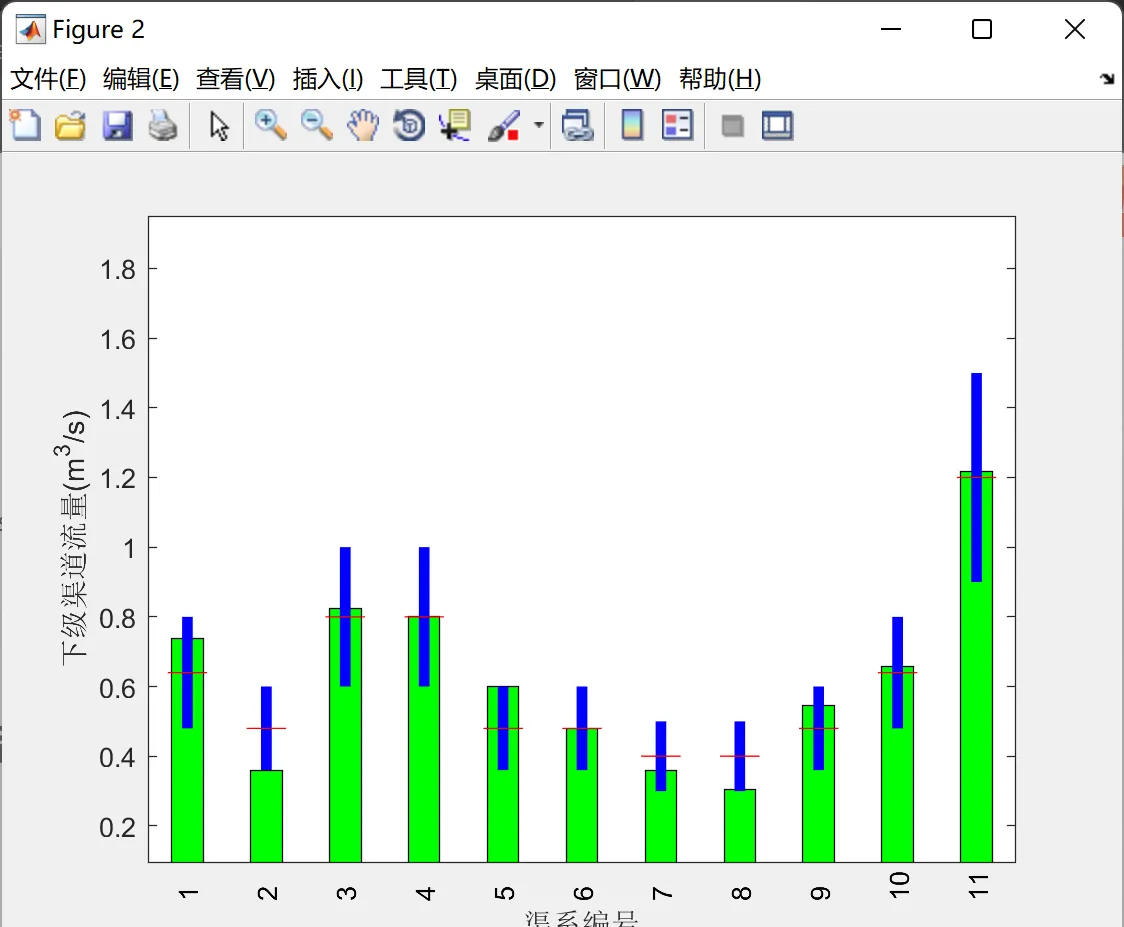
2 運作結果

👨‍🎓部落客課外興趣：中西方哲學，送予讀者：

👨‍💻做科研，涉及到一個深在的思想系統，需要科研者邏輯缜密，踏實認真，但是不能隻是努力，很多時候借力比努力更重要，然後還要有仰望星空的創新點和啟發點。當哲學課上老師問你什麼是科學，什麼是電的時候，不要覺得這些問題搞笑，哲學就是追究終極問題，尋找那些不言自明隻有小孩子會問的但是你卻回答不出來的問題。在我這個專欄記錄我有空時的一些哲學思考和科研筆記：​​科研和哲思。​​建議讀者按目錄次序逐一浏覽，免得驟然跌入幽暗的迷宮找不到來時的路，它不足為你揭示全部問題的答案，但若能讓人胸中升起一朵朵疑雲，也未嘗不會釀成晚霞斑斓的别一番景緻，萬一它居然給你帶來了一場精神世界的苦雨，那就借機洗刷一下原來存放在那兒的“真理”上的塵埃吧。

3 參考文獻

4 Matlab代碼實作

function offspring=Mutate(population,state)
% 本函數完成變異操作
global T Qmax Qmin
N=length(population);

if state<0.5
    
    offspring1 = population;
    for i=1:N
        pop1 = population(i);
        pop2 = population(randperm(N,1));
        
        % 随機挑選1-2個位置進行交叉操作
        pos = randperm(11,randi([1,3],1));
        pop1.tstart(pos) =  pop2.tstart(pos);
        pop1.tend(pos) =  pop2.tend(pos);
        pop1.q(pos) =  pop2.q(pos);
        
        offspring1(i) = pop1;
    end
    
    
    offspring2 = population;
    for i=1:N
        pop1 = population(i);
        % 開始時間
        pos = randperm(11,randi([1,2],1));
        pop1.tstart(pos) = pop1.tstart(pos) + randi([-2,2],size(pos));
        pop1.tstart(pos) = max(pop1.tstart(pos),1);
        pop1.tstart(pos) = min(pop1.tstart(pos),T*24/4-1); %修複上下界
        pop1.tend(pos) = max(pop1.tstart(pos),pop1.tend(pos));
        
        offspring2(i) = pop1;
    end
    
    offspring3 = population;
    for i=1:N
        pop1 = population(i);
        
        % 結束時間
        pos = randperm(11,randi([1,2],1));
        pop1.tend(pos) = pop1.tend(pos) + randi([-2,2],size(pos));
        pop1.tend(pos) = max(pop1.tstart(pos),pop1.tend(pos));
        pop1.tend(pos) = min(pop1.tstart(pos),T*24/4); %修複上下界
        offspring3(i) = pop1;
    end
    
    offspring = CalObj([offspring1,offspring2,offspring3]);
else
    
    offspring4 = population;
    for i=1:N
        pop1 = population(i);
        
        % 供水量
        pos = randperm(11,randi([1,2],1));
        pop1.q(pos) = pop1.q(pos) + 0.2.*rands(1,length(pos));
        pop1.q = max(Qmin,pop1.q);
        pop1.q = min(Qmax,pop1.q); %修複上下界
        offspring4(i) = pop1;
    end
    offspring = CalObj(offspring4);
end