K-th Number HDU - 6231(二分+尺取)

K-th Number HDU - 6231

Alice are given an array A[1…N] with N numbers.

Now Alice want to build an array B by a parameter K as following rules:

Initially, the array B is empty. Consider each interval in array A. If the length of this interval is less than K, then ignore this interval. Otherwise, find the K-th largest number in this interval and add this number into array B.

In fact Alice doesn’t care each element in the array B. She only wants to know the M-th largest element in the array B

. Please help her to find this number.

Input

The first line is the number of test cases.

For each test case, the first line contains three positive numbers N(1≤N≤105),K(1≤K≤N),M. The second line contains N numbers Ai(1≤Ai≤109)

.

It’s guaranteed that M is not greater than the length of the array B.

Output

For each test case, output a single line containing the M-th largest element in the array B

.

Sample Input

2
5 3 2
2 3 1 5 4
3 3 1
5 8 2
           

Sample Output

3
2
           

題意：

給你數列A，對于A的每一個區間，求第K大，插入到數列B中，最後再求數列B的第M大！

分析：

首先二分答案，每次二分的時候我們得到一個x，這個時候我們利用尺取，去得到第K大數大于等于x的區間一共有多少個，具體操作如下

我們從頭開始記錄a[i] >= x的個數，當恰好有k個數大于等于x了，這個時候假如說就是到下标i的時候恰好有k個數大于等于x了，那麼區間[1,i]内一定能夠作為一個區間，找到一個第K大數大于等于x，那麼同理我保持前面不動，向後一個一個的擴充，也一定能找到第K大的數大于等于x，即在區間[1,i+1],[1,i+2],[1,i+3]…[i,n]，是以這些區間都可以找到第K大的數大于等于x，而後面這些區間的個數為n-i，再加上[1,i]這個區間，那麼此時共有n-i+1個區間其第K大的數大于等于x。

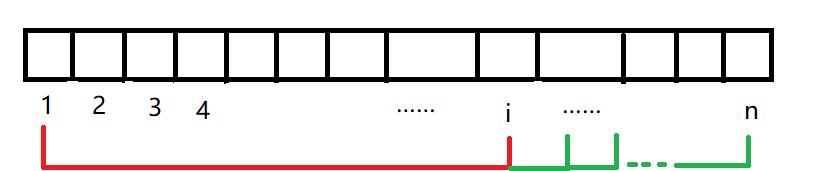
那麼隻有這些嗎，我們定義下标j，讓j從頭開始，即從1開始，往後移動，如果a[j] < x,那麼這個數a[j]對于能否取到第K大的數大于等于x沒有影響，因為它比x小嗎，取肯定不會取它，是以這個時候我們可以去掉它，以下一個為開始，這樣相當于起點變了，但是終點還是i呀，是以所有可以的區間還是[j,i],[j,i+1],[j,i+1]…[j,n]，而且區間[j,i]中仍然後k個大于等于x的數，沒有變，是以我們區間個數還是加上n-i+1，這個過程while循環即可，知道a[j] >= x停止，否則可以一直進行

如果這個時候a[j]是一個大于等于x的數，即a[j] >= x，此時我們停止循環，因為我們要減掉這個數，從下一個開始，是以循環停止後，j++，表示從下一個開始，而且大于等于x的個數要減1，這個時候，我們就得變化終點i了，i往後尋找當找到又一個大于等于x的時候，個數加1，如果總個數又等于K個了，那麼重複上面的操作就行了。

這樣我們就可以求得第K大數是大于等于x的區間一共有多少個，如果大于等于M個說明我們枚舉的x數小了，有太多第k大大于等于x了，是以二分答案保留右區間，否則保留左區間，知道最後，x就是答案。

code：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int N,K;
ll M;
int a[100005];

bool judge(int x){
    ll ans = 0;
    int num = 0;
    int j = 1;
    for(int i = 1; i <= N; i++){
        if(a[i] >= x)
            num++;
        if(num == K){
            ans += N - i + 1;
            while(a[j] < x){
                ans += N - i + 1;
                j++;
            }
            num--;
            j++;
        }
    }
    if(ans >= M)
        return true;
    else
        return false;
}
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d%lld",&N,&K,&M);
        for(int i = 1; i <= N; i++){
            scanf("%d",&a[i]);
        }
        int l = 1,r = 1000000000;
        int m;
        while(l < r){
            m = l + r >> 1;
            if(judge(m))
                l = m + 1;
            else
                r = m;
        }
        printf("%d\n",l-1);
    }
    return 0;
}