四面體體積求法

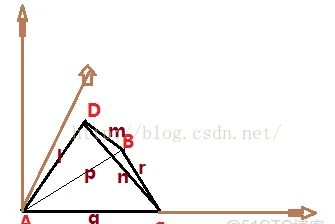
四面體（三棱錐）體積 ：

設

有：

不過這是有向的。如果知道那四個頂點，用這個公式即可求出體積。

如果不知道四點僅知道6條邊長，就得用下面的方法——歐拉四面體公式

寫成行列式：

那麼有：

轉置：

行列式乘法：

其中，

因為：

是以：

有：

進一步簡化：

題目：

HDU 1411

​​http://acm.hdu.edu.cn/showproblem.php?pid=1411​​

大意：給出6邊求出四面體的體積

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

int main()
{
    //freopen("cin.txt","r",stdin);
    double p,q,l,r,m,n;
    while(~scanf("%lf%lf%lf%lf%lf%lf",&p,&q,&l,&r,&m,&n)){
        double part1=p*p+q*q-r*r;  //p*p*q*q*l*l;
        double part2=q*q+l*l-n*n;
        double part3=l*l+p*p-m*m;
        double ans=4*p*p*q*q*l*l+part1*part2*part3-q*q*part3*part3-l*l*part1*part1
           -p*p*part2*part2;
        ans=sqrt(ans/144);
        printf("%.4lf\n",ans);
    }
    return 0;
}      

POJ 2208

​​http://poj.org/problem?id=2208​​

用同樣的思路此題卻過不了了。神奇！！

查閱資料發現，另一種方案可行：

設 ：

有：

S=

證明來自：

​​http://wenku.baidu.com/link?url=x-Jy7p-0Iqz75PUSM-iFl4WhXmBY01bFstGCGfmxVCPmUk-pyhTPNB1jmpSSAJaI-jSOlpIs-2dpggmUAZnEN4qwWOYt9By7wuyd446B2SC​​

而要AC的代碼也挺奇葩，

樣例的計算結果：

1999.9937

AC了

難道這就是所謂的special judge？

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

int main()
{
    //freopen("cin.txt","r",stdin);
    double p,q,l,r,m,n;
    while(~scanf("%lf%lf%lf%lf%lf%lf",&p,&q,&l,&r,&m,&n)){
        double A=acos((p*p+q*q-r*r)/(2*p*q));  
        double B=acos((p*p+l*l-m*m)/(2*p*l));
        double R=acos((q*q+l*l-n*n)/(2*q*l));
        double P=(A+B+R)/2;
        double ans=p*q*l/3*sqrt(sin(P)*sin(P-A)*sin(P-B)*sin(P-R));
        printf("%.4lf\n",ans);
    }
    return 0;
}