【題解】最大子段和

題目描述

給出一個長度為 n 的序列 a，選出其中連續且非空的一段使得這段和最大。

輸入格式

第一行是一個整數，表示序列的長度 n。

第二行有 n 個整數，第 i 個整數表示序列的第 i 個數字 aia_iai​。

輸出格式

輸出一行一個整數表示答案。

輸入輸出樣例

輸入 #1

7
2 -4 3 -1 2 -4 3           

複制

輸出 #1

4           

複制

說明/提示

樣例 1 解釋

選取 [3,5] 子段 {3,−1,2}，其和為 4。

資料規模與約定

• 對于 40% 的資料，保證

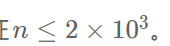
• 對于 100% 的資料，保證

題目分析

尺取法的本質是對連續區間的維護，被維護的區間符合某種條件。右指針相當于把元素加入到這個區間，左指針相當于把元素從區間内去除。除了之前題目中的雙指針，騎士也能夠用隊列來進行處理，又或者是具有相似概念的東西。

仔細閱讀題目，可發現題目要求的是連續且非空的最大子段和。

若用暴力方式處理複雜度為

根據資料範圍明顯不可取。此時，可發現又是一個對連續區間的維護問題，那麼我們嘗試從其他的角度進行思考。

該區間元素必須連續，那麼當碰見一個新的元素，無非出現兩種情況：

1. 該元素與之前的連續區間加起來的和比較大
2. 該元素與之前的連續區間加起來的和還沒有這個元素本身大

如果是情況1，那麼連續區間總和就加上新增元素。而如果是情況2，則将該元素作為新的連續區間總和。在過程中再不斷更新最大連續區間和即可。

由于隻需周遊每個元素一次，時間複雜度為O(n)。

代碼實作

#include <iostream>
#include <cstdio>
using namespace std;
int a;
/*
連續序列和
1. 目前元素
2. 和前面的一段組成新序列
*/
int main(){
    int n;
    int sum=0;//連續序列和
    int ans=-1e9;//最大連續序列和
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a;
        if(sum+a<a){//判斷是a與前面的連續序列加起來大還是單獨一個元素更大
            sum=a;//單獨的元素更大
        }else{
            sum+=a;//加起來更大
        }
        ans=max(ans,sum);//更新過程中的最大連續序列和
    }
    cout<<ans;//輸出答案
    return 0;
}           

複制

Q.E.D.