在大學的學習中,一開始自認為已經學會了反碼與補碼,但在看到多種表述之後,反而是越來越亂,疑惑越來越多,即使記住了之後又會混淆,今天又看到了一次,為了防止以後再次忘記,寫這篇部落格記錄一下(記錄過程依據《數字電子技術(第十版)》,中英文結合)
首先從最一般的意義上,分别說一下二進制的反碼和補碼:
1、反碼 (1’s complement)
把所有的0變為1,所有的1變為0。
如:
10110010 Binary number
01001101 1’s complement
2、補碼 (2’s complement)
在反碼的最低有效位上加1。
補碼 = 反碼 + 1
另一種求補碼的方法:
- 從右邊的最低有效位開始,往左邊寫下它們實際的位,直到遇到第一個1(包括1)
- 左邊剩下的位求反碼
如:
1011 1000 Binary number
0100 1000 2’s complement
這是在不區分正負數的情況下泛泛而談的,其側重點在于反碼與補碼如何操作,但實際上反碼和補碼的作用是用在帶符号數上面的,下面進入重點。
3、帶符号數 Signed Number
3.1 符号位 The Sign Bit
帶符号的二進制的最左邊的那一位就是符号位,指出這個數為正數還是負數,0表示正數,1表示負數。
下面介紹幾種表示帶符号數的形式。
3.2 符号數值的形式 Sign-Magnitude Form
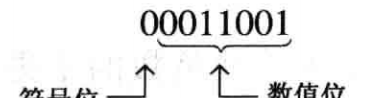
最左邊的一位是符号位,剩餘的位都是數值位。其實也就是一般的帶符号數的形式,數值位對于正數和負數來說都是二進制源碼(in true (uncomplemented) binary)。如十進制數 +25 使用符号數值形式表示成8位帶符号二進制數為:
十進制數 -25 表示為:
他們之間的唯一差別就是符号位不同。
3.3 反碼形式 1’s Complement Form
正數的反碼形式:與符号數值形式相同;
負數的反碼形式:相應正數的反碼。也就是為相應正數的符号數值形式的每一位取反。
應當注意的是并不是帶符号數的反碼都是每一位取反。
反碼和補碼其實是為了解決正數和負數的加減法運算的,是以正數其實不用做什麼改變,而負數改變形式後可以巧妙解決一些運算問題。比如減去某個數和加上這個數的補碼是一樣的,這就是為什麼計算機在所有的算術運算中都使用補碼來表示負整數。
了解了反碼是帶符号數的一種表示形式及其目的,大概就能了解為什麼正數的反碼是其本身,下面要說到的補碼也是一樣的道理。
舉例:在反碼表示形式中,
十進制數 25 表示為:
00011001
十進制數 -25 表示為:
11100110
3.4 補碼形式 2’s Complement Form
正數的補碼形式:與符号數值形式相同;
負數的補碼形式:負數的反碼加1。
舉例:在補碼表示形式中,
十進制數 25 表示為:
00011001
十進制數 -25 表示為:
11100111
3.5 總結
對于帶符号數,
正數的反碼和補碼與原碼相同;
負數的反碼等于相應正數的反碼,補碼等于相應正數的補碼。
但這樣的說法是會讓人産生疑惑的,因為既然正數的反碼等于原碼,且負數的反碼等于相應正數的反碼(即等于正數的原碼),那正數負數的表示不就一樣了。我也覺得這種說法很有歧義,但如果把第二個反碼看成是一種廣義上的操作,即把每一位取反,這樣就沒問題了,總之隻要能了解就好,有時候反碼就是真的“反”碼,實實在在的操作。但為了避免這種困惑,倒不如表述得更清楚直接些:
對于帶符号數,
正數的反碼和補碼與原碼相同;
負數的反碼等于相應正數的符号數值形式的各個位取反,補碼等于反碼加1。
如有不合理的地方,歡迎指正。