1. 期望
期望也就是平均值,是一個數值,反應的是随機變量平均取值的情況,期望也叫做權重平均。在信号中代表直流分量。
當随機變量X滿足均勻分布時,對一段長度為N的離散序列X=x[n],n=0,1,2….N-1,其期望E(X)計算過程為:
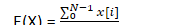
舉例子:對于長度為10的離散型随機變量X=sin(t),取一個周期,求數學期望E(X).
這就是求正弦信号在一個周期内的均值。
2. 有效值(均方根值RMS,root-mean-square)
有效值也是也個數值,又叫均方根,我們以X=Asin(t)這個信号為例。最大值Vmax=A,峰峰值Vpp=2A,假設此電壓信号作用于一個電阻為1Ω的負載,根據焦耳定律:
對于一個周期的正弦信号X=Asin(t)而言,我們計算它在一個周期2π的時間内産生的熱量,還要對時間進行積分,即:
假設在相同時間2π内,有一等效直流電壓Y作用于R=1Ω的電阻,其産生的熱量:
所謂有效值,指的是此直流電壓Y産生的熱量等效于交流電Asin(t)産生的熱量,二者效果一樣,所有叫有效值。
取Q2=Q,
推廣上面的計算過程,對于離散序列,可以得到均方根一般計算公式:
3. 均方值
RMS的平方就是均方值MS(mean-square value),意思是均方根值的開方。
4. 方差
方差是一個具體的數,符号為,
衡量的是各資料偏離平均值的大小,是偏離值平方的平均值(有點拗口)。
方差越小,資料越集中,偏離程度越高;
方差越大,資料越分散,偏離程度越低;
對于一段長度為N的離散序列X[n],其平均值(期望)為E,則方差:
有的同學看到方差的另一種計算公式:
為什麼分母有N-1和N的差別呢?
N-1對應的是無偏估計;N對應有偏估計,其方差<=真值方差。matlab函數var預設使用的是N-1的無偏估計計算方法。
使用無偏估計,對正弦信号X = sin(t)求方差,結果為0.5556;
使用有偏估計,求的方差為0.5
5.标準差(Standard Deviation)、均方差
标準差是把方差取根号得到的。
因為方差與處理的資料的量綱有差異,是以有時我們用标準差來描述資料偏離程度。
6. 均方誤差,MSE(Mean Squared Error)
和方差很像,差別在于MSE關注的是預測資料與真實值的偏離程度。
方差是資料與均值的偏離程度。
f表示預測值,y表示真實值。
7. 均方根誤差RMSE
8. 協方差Cov
協方差表示兩個變量之間有關系,定義式為:
Cov(X,Y) = E{[X-E(X)][Y-E(Y)]}
上面的計算過程比較麻煩,有更簡單的計算公式:
Cov(X,Y) = E{[X-E(X)][Y-E(Y)]}=E(XY) - E(X)E(Y)
強調一點:事件X、Y互相獨立,則Cov(X,Y)=0;
反之,Cov(X,Y)=0,X、Y不一定互相獨立。
舉例子,對于X=sin(t)和Y=0.5+0.5sin(t)兩個離散序列。求其協方差:
為0.25,如果直接調用matlab函數計算:cov(X,Y)結果是0.2778
因為matlab使用的是無偏計算公式,前文有介紹,此處不多講。
加微信[chunhou0820],擷取源代碼
9.相關系數
協方差隻表示兩個事件有關系,數值可以大于1也可以小于1,怎麼評估具體關系程度呢?引入相關系數概念,matlab函數為:corr或corrcoef
|ρ|≤1;
ρ=±1,表示兩個變量線性相關
ρ=0,表示兩個變量無關
ρ=other,表示兩個變量有些關系
相關系數計算公式如下,各參數前文一一介紹過:
我們計算離散信号X=sin(t)和Y=0.5+0.5*sin(t)相關系數;
得到相關系數為1,說明二者完全線性相關,即:Y=0.5+0.5X。
如果使用matlab自帶函數求解,結果是一樣的。
如果把Y換為Y=0.5*sin(t+0.5),則求解到的相關系數為0.8776,說明二者非常接近線性相關。
10. 自相關函數
顧名思義,這是一個函數,上面介紹那些參數名額都是具體的數值,從現在開始是介紹函數。下面是自相關函數的求解公式。描述的是同一個信号在不同時刻的相關程度,matlab公式為xcorr。
有什麼作用呢?比如你有一個帶噪的信号Y,其中既有有用的信号X,也有噪聲N,噪聲太強烈,信噪比很低淹沒了正弦信号,就可以用自相關函數提取出X的資訊。
Y=X+N=sin(t)+noise(t),
下圖第一行為原始帶噪的信号,我們完全區分不出來其中的正弦信号;
第二行為求解得到的自相關函數;第三行為隐藏在噪聲中的sin(t)信号,可以看出求解自相關函數後,可以得到一個比較幹淨的信号,其頻率和目标信号sin(t)頻率一樣。
11. 互相關函數
把自相關函數計算過程稍微變化,則得到求解互相關函數的計算公式:
matlab函數為[a,b]=xcorr(X,Y,'unbiased');
求互相關的過程和卷積灰常灰常像,是以求卷積的過程也可以認為是求相關。