這應該是過采樣系列的最後一篇文章,經常有同學在使用FPGA、單片機或者DSP進行過采樣時沒有正确設計代碼,導緻結果異常,有些結果看似正常,而實際卻沒有意義。
這篇文章涉及到簡單的整型資料和算術運算,希望能有所幫助,僅供參考。
舉栗子,理想的8 bit ADC,編碼範圍是0-255,在參考電壓是255mV的情況下,分辨率是1mV。
對一個理想的9.6mV直流電壓進行采樣,ADC無法分辨小數點後的0.6mV,采樣結果會被編碼為10,即10mV。
過采樣有效是有前提條件的,在這裡是對9.6V的直流電壓加随機噪聲。
過采樣
對疊加噪聲後的信号進行4次采樣,理論上應該得到[9.8, 9.6, 10.4, 9.6]4個離散的樣本點,而受到ADC分辨率的限制,實際隻能得到[10, 10, 10, 10]4個編碼樣本,所有樣本點都隻能分布在。。。8、9、10。。。整數上。
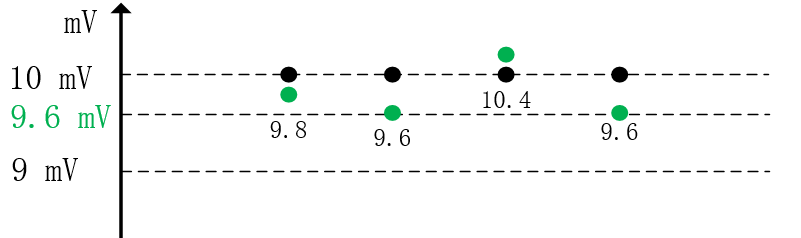
接下來就對這4個樣本點詳細介紹,直覺的感受過采樣的原理。
假設信号帶寬為B,我們分别分析采樣頻率F為2B sps/S和8B sps/S兩種情況。
當采樣頻率為2B時,過采樣率OSR1=F/(2B)=1;
當采樣頻率為8B時,過采樣率OSR4=F/(2B)=4;
OSR4/OSR1=4,即過采樣率提高了4倍(注意:是提高了4倍),其分辨率應該會增加1bit。
過采樣系列一:采樣定理與過采樣率
繼續以上面采樣9.6mV信号舉栗子。
當以采樣頻率F=1采樣時,采集的結果是[10, 10,10, 10]中的任意一個,對應二進制(0000 1010)。
當以采樣頻率F=4采樣時,采集的結果是[10, 10,10, 10]4個序列。
下面對F=4的4個資料進行下抽處理(降采樣),可以減少計算量增加分辨率。
抽取
ADC是8bit的分辨率,但是在過采樣計算時,不能定義并初始化一個8bit的整形資料,如果初始化8bit的資料,計算過程會溢出,最終結果的位寬還是8bit,并沒有增加分辨率,在這裡我們定義一個16bit的資料,預留了足夠的buffer。
對采樣得到的4個8bit資料求和運算,需要計算最大位寬,求和後的最大位寬為8+2=10bit,相當于左移了2bit,變為10bit。
如果隻是簡單的求平均,求和後的結果再除以采樣個數4的話,則資料其實是右移2bit,又變回原來的8bit位寬,并沒有增加分辨率。
在這裡我們選擇下抽方法是求和後除以2,即右移1bit,則資料從10bit變為9bit,相比于原始的8bit,增加了1bit分辨率(過采樣容易了解,更重要的是下抽)。
過采樣系列三:量化誤差與過采樣率
過采樣率為4時,采樣的4個資料序列[10, 10,10, 10]求和後是40,對應二進制(00 0010 1000),右移1bit後變為20,對應二進制(0 0001 0100)
255mV參考電壓下,原始的8bit ADC,分辨率為1mV,采集的資料是9(0000 1001),即9mV;
過采樣率增加4倍後:
255mV參考電壓下,9bit ADC,分辨率為0.5mV,采集的資料是20(0 0001 0100),即10.0(9.98)mV;
過采樣率增加4倍的前提下,隻提高了1bit分辨率,效果不是很明顯,繼續在9.6mV基礎上添加随機噪聲,這次過采樣率再增加4倍,達到16倍,即采樣速率F=16,對16個采樣序列進行計算舉例。
對采樣得到的16個8bit資料求和運算,最大位寬是8+4=12bit。
求和:10*8+9*7+11=154,對應二進制是(0000 1001 1010),再右移2bit,則變為10bit的38(00 0010 0110),(再次強調,不能簡單的求和然後求平均)。
9.6mV加噪信号:
1、255mV參考電壓下,原始的8bit ADC,分辨率為1mV,采集的資料是10(0000 1001),即10mV
2、過采率為4後:
255mV參考電壓下,9bit ADC,分辨率為0.5mV,采集的資料是20(0 0001 0100),即10.0(9.98)mV;
3、過采率為16後:
255mV參考電壓下,10bit ADC,分辨率為0.25mV,采集的資料是38(00 0010 0110),即9.47mV;
從列舉的例子可以看出,過采樣率是可以提高分辨率的,但是提高采樣速率來提高分辨率的代價是巨大的(牛頓第三定律:得到點東西時總要舍棄點什麼^_^)。