KMP算法,又稱作“看貓片”算法(誤),是一種改進的字元串模式比對算法,可以在O(n+m)的時間複雜度以内完成字元串的比對操作,其核心思想在于:當一趟比對過程中出現字元不比對時,不需要回溯主串的指針,而是利用已經得到的“部分比對”,将模式串盡可能多地向右“滑動”一段距離,然後繼續比較。
KMP(看貓片)算法
![]()
1. 樸素的字元串模式比對算法
求一個字元串(模式串)在另一個字元串(主串)中的位置,稱為字元串模式比對。
在樸素的字元串模式比對算法中,我們對主串S和模式串T分别設定指針i和j,假設字元串下标從0開始,初始時i和j分别指向每個串的第0個位置。在第n趟比對開始時,i指向主串S中的第n-1個位置,j指向模式串T的第0個位置,然後逐個向後比較。若T中的每一個字元都與S中的字元相等,則稱比對成功,否則,當遇到某個字元不相等時,i重新指向S的第n個位置,j重新指向T的第0個位置,繼續進行第n+1趟比對。
例如,我們對模式串T=“abaabcac”和主串S=“abcabaabaabcacb”進行比對。如圖1.1,此時正在進行第4趟比對,S[3...7]與T[0...4]均相等,但當i=8,j=5時,S[8]與T[5]不相等,比對失敗。于是,置i=4,j=0,相當于将模式串向右移動一位後,重新開始下一趟比對,如圖1.2。

圖1.1 當i=8,j=5時,字元不相等,比對失敗
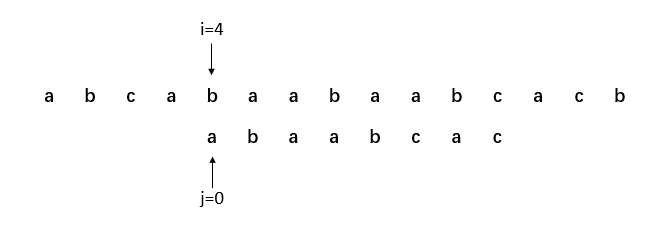
圖1.2 将模式串向右移動一位後,重新開始下一趟比對
利用此種方法進行字元串比對,最壞情況下時間複雜度為O(n*m),其中n和m分别為主串和模式串的長度。
2. 改進的字元串模式比對算法——KMP算法
在上面的例子中,我們可以看到,當i=8,j=5時,S[8]與T[5]不相等,于是置i=4,j=0,相當于将模式串向右移動一位,再開始下一趟比對。然而,通過觀察我們可以發現,之後的兩趟比對,即i=4,j=0以及i=5,j=0都是不必要的。這是因為,在之前的一趟比對過程中,我們已經部分比對了T的子串“abaab”。此時将T向右移動一位,則相當于對T中的“abaab……”與S中的“baab……”進行比對,顯然無法比對成功。繼續右移T,則相當于對T中的“abaab……”與S中的“aab……”進行比對,依然無法比對成功。隻有當T向右移動3位後,此時對T中的“abaab……”與S中的“ab……”進行比對,才會有成功的可能,也就有必要向後繼續進行比較。如圖2.1。

圖2.1 比對失敗時,将T向右移動3位後,才有繼續比較的必要
是以,當i=8,j=5,T的子串“abaab”已經比對成功,而其後一位字元卻不相等時,不必回溯i指針,置i=8,j=2,繼續向後比較,相當于将T向右移動3位,并從T的第3位開始向後比較。如圖2.2。
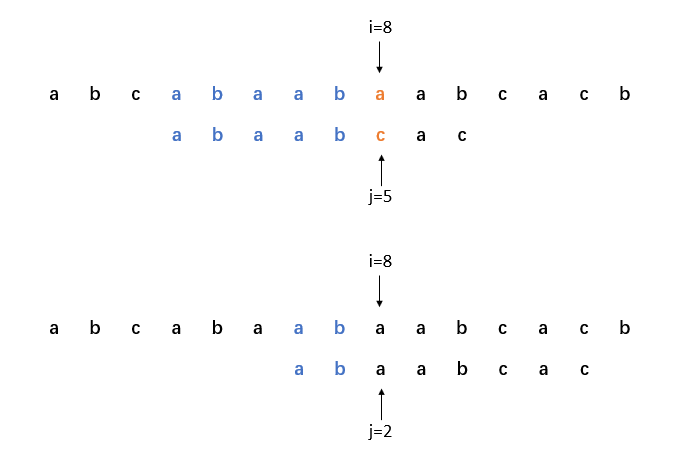
圖2.2 比對失敗後,直接置i=8,j=2,繼續向後比較
這就是KMP算法的基本思路。對于模式串T中的前j個字元組成的子串,設定數組next[j]存放一個值,當模式串T比對至第j個字元時與主串不相等,則i指針不變,将j指針置為next[j]的值,然後繼續進行比較。在上例中,串“abaab”為模式串T的前5個字元組成的子串,令next[5]=2,當i=8,j=5時,S[8]與T[5]不相等,于是置i=8,j=next[j]=next[5]=2,然後繼續進行比較。
是以,KMP算法的核心在于求出數組next,即模式串T中每一個長度為j (0
next數組求解算法
在求解next數組前,我們首先需要了解next數組的含義。回到前面的例子,當T的子串“abaab”的下一個字元與主串不相等時,主串的指針i不變,j回溯至2,指向T的第3個字元,其本質是因為串“abaab”的字首和字尾有一個長度為2的最長公共串“ab”,是以我們省略了字首“ab”和字尾“ab”的比較過程,直接對它們的後一個字元,即T[2]和S[8]進行比較。
再看另一個例子,假設有模式串T=“abacaabadad”,其已部分比對完T[0...7],即“abacaaba”,在比對T[8]時遇到比對失敗,因T[0...7]的字首和字尾有長度為3的最長公共串“aba”,是以next[8]=3,置j=next[j]=next[8]=3,i不變,然後從T[3],即T的第4個字元開始比較。如圖2.3。
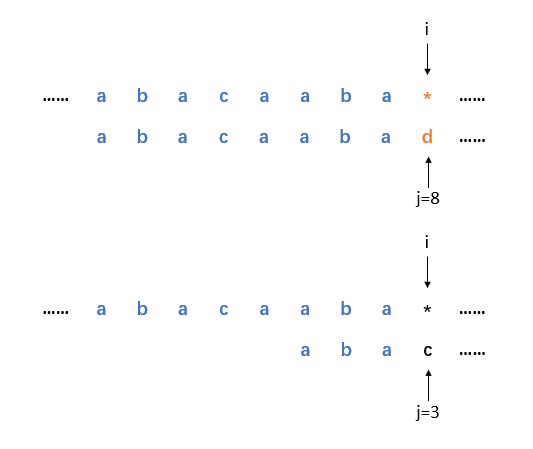
圖2.3 比對T[8]時失敗,i不變,j回溯至3
總之,對于模式串T,next[j]代表了T的前j個字元組成的子串中,其字首和字尾的最長公共串的長度。
求解字元串T的next數組的算法如下:
next[0]=-1, next[1]=0。
在求解next[j]時,令k=next[j-1],
比較T[j-1]與T[k]的值,
a. 若T[j-1]等于T[k],則next[j]=k+1。
b. 若T[j-1]不等于T[k],令k=next[k],若k等于-1,則next[j]=0,否則跳至3。
下面以模式串T=“abaabcac”為例,給出求next數組的過程:
next[0]=-1, next[1]=0。
當j=2時,k=next[j-1]=next[1]=0,由于T[j-1]=T[1]=‘b’,T[k]=T[0]=‘a’,T[j-1]不等于T[k],令k=next[k]=next[0]=-1,是以next[2]=0。
當j=3時,k=next[j-1]=next[2]=0,由于T[j-1]=T[2]=‘a’,T[k]=T[0]=‘a’,T[j-1]等于T[k],是以next[3]=k+1=1。
當j=4時,k=next[j-1]=next[3]=1,由于T[j-1]=T[3]=‘a’,T[k]=T[1]=‘b’,T[j-1]不等于T[k],令k=next[k]=next[1]=0。此時T[k]=T[0]=‘a’,T[j-1]等于T[k],是以next[4]=k+1=1。
當j=5時,k=next[j-1]=next[4]=1,由于T[j-1]=T[4]=‘b’,T[k]=T[1]=‘b’,T[j-1]等于T[k],是以next[5]=k+1=2。
當j=6時,k=next[j-1]=next[5]=2,由于T[j-1]=T[5]=‘c’,T[k]=T[2]=‘a’,T[j-1]不等于T[k],令k=next[k]=next[2]=0。此時T[k]=T[0]=‘a’,T[j-1]不等于T[k],再令k=next[k]=next[0]=-1,是以next[6]=0。
當j=7時,k=next[j-1]=next[6]=0,由于T[j-1]=T[6]=‘a’,T[k]=T[0]=‘a’,T[j-1]等于T[k],是以next[7]=k+1=1。
将next數組全部求出之後,隻需在簡單的比對算法上稍作修改,便得到了KMP的比對算法:當模式串T比對至第j個字元時比對失敗,i指針不變,将j指針置為next[j]的值,若j的值為-1,則将i和j同時加1。随後繼續進行逐個的比較。
下面以模式串T=“abaabcac”和主串S=“abcabaabaabcacb”進行比對為例,給出KMP比對算法的全過程。
之前已經求得模式串T的next數組為[-1, 0, 0, 1, 1, 2, 0, 1]。
初始時,i=0,j=0,比對成功。

2. i=1,j=1,比對成功。
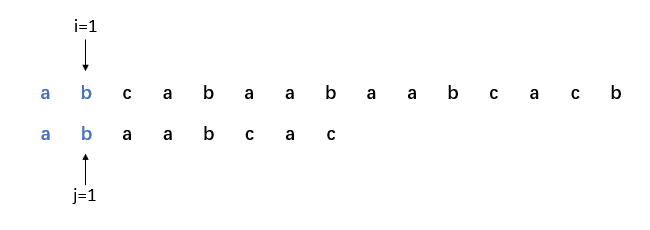
3. i=2,j=2,比對失敗。

4. i=2,j=next[2]=0,比對失敗。

5. i=2,j=next[0]=-1,比對失敗。

6. i=2+1=3,j=-1+1=0,比對成功。
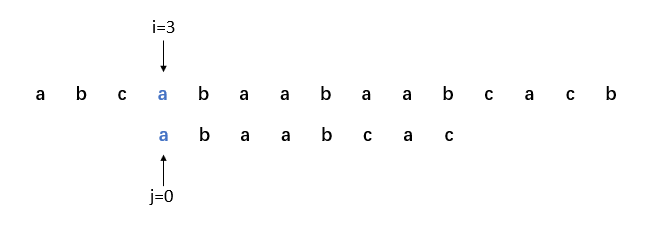
7. i=4,j=1,比對成功。
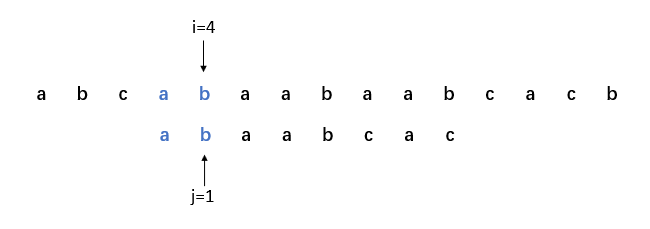
8. i=5,j=2,比對成功。
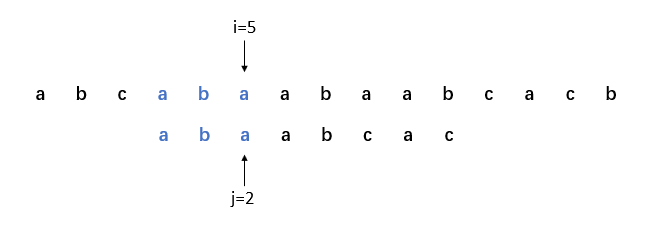
9. i=6,j=3,比對成功。
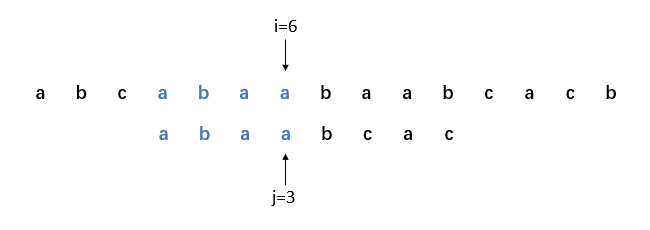
10. i=7,j=4,比對成功。
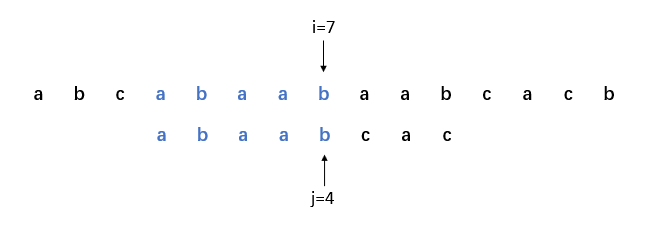
11. i=8,j=5,比對失敗。

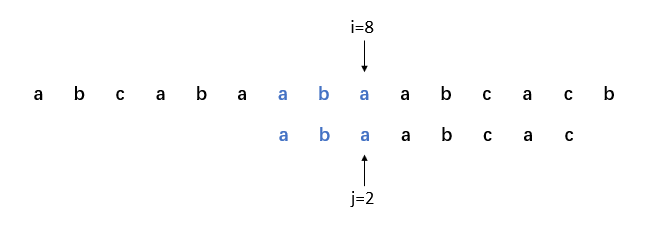
12. i=8,j=next[5]=2,比對成功。
13. 繼續向後比較,中間過程均比對成功,故不再贅述,當i=13,j=7時,模式串比對完成。

以上就是KMP比對算法的全過程。總結一下,KMP算法的實質就是以空間換時間,在比對之前将模式串的一些資訊存儲起來(next數組),在随後的比對過程中利用這些資訊減少不必要的比對次數,以提高比對效率。在實際的應用過程中,簡單模式比對算法的執行時間常常接近于KMP算法,僅當主串與模式串有很多“部分比對”時,KMP算法才能顯著提升性能。
3. KMP算法的Java實作
下面給出KMP算法的Java代碼。整個算法分為兩部分,一是next數組的求解,二是KMP比對過程。
public class KMP {
public static int[] getNextArray(char[] t) {
int[] next = new int[t.length];
next[0] = -1;
next[1] = 0;
int k;
for (int j = 2; j < t.length; j++) {
k=next[j-1];
while (k!=-1) {
if (t[j - 1] == t[k]) {
next[j] = k + 1;
break;
}
else {
k = next[k];
}
next[j] = 0; //當k==-1而跳出循環時,next[j] = 0,否則next[j]會在break之前被指派
}
}
return next;
}
public static int kmpMatch(String s, String t){
char[] s_arr = s.toCharArray();
char[] t_arr = t.toCharArray();
int[] next = getNextArray(t_arr);
int i = 0, j = 0;
while (i
if(j == -1 || s_arr[i]==t_arr[j]){
i++;
j++;
}
else
j = next[j];
}
if(j == t_arr.length)
return i-j;
else
return -1;
}
public static void main(String[] args) {
System.out.println(kmpMatch("abcabaabaabcacb", "abaabcac"));
}
}
參考資料及緻謝
在學習KMP算法思路的過程中,我大量參考了“王道考研系列”的《資料結構聯考複習指導》一書,以及CSDN部落客v_JULY_v的文章:從頭到尾徹底了解KMP,特此鳴謝。
同時感謝微網誌部落客@回憶專用小馬甲和實驗室的大紅袍CocoXu提供的大量貓片,讓我在學習KMP算法的過程中擁有持續的動力。
文章中如有錯誤,歡迎指正!