hdu 1698 Just a Hook(線段樹 - 區間修改 區間查詢)

連結:http://acm.hdu.edu.cn/showproblem.php?pid=1698

來源:hdu

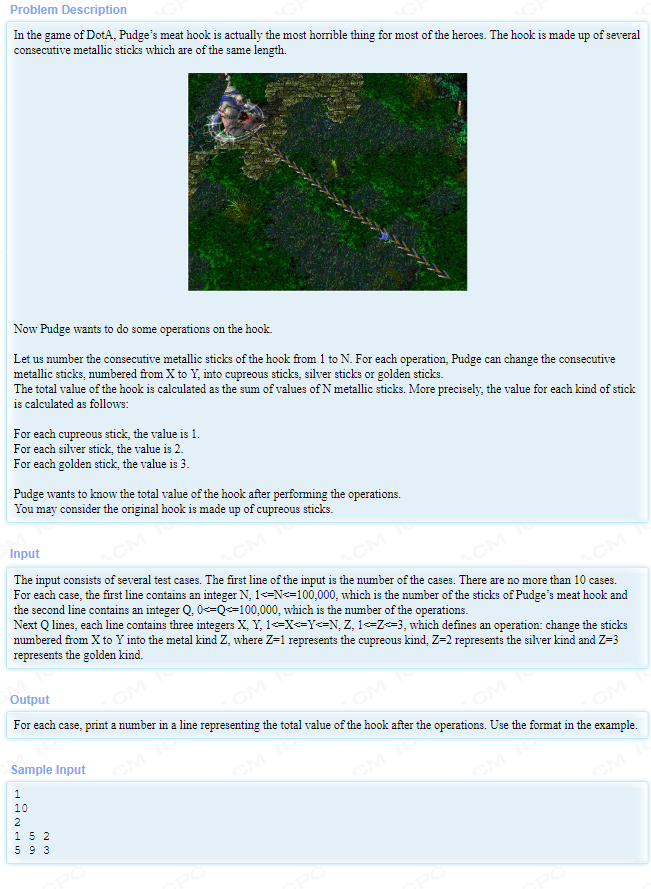
  題意:給出一個N,區間中初始值為1,輸出m代表m次修改,将區間[l,r]修改為v,輸出最終這個序列的總和。

#include<bits/stdc++.h>
#define LNode x<<1
#define RNode x<<1|1
using namespace std;

typedef long long ll;
typedef pair<int,int>P;
const int Max_n=1e5+10;
const int inf=0x3f3f3f3f;
int sum[4*Max_n];int a[Max_n],tag[4*Max_n],Min[4*Max_n],cnt[Max_n*4];

void build(int l,int r,int x){//建構線段樹(自頂向下)
    if(l==r){ sum[x]=a[l]; return ; }
    int mid=l+((r-l)>>1);
    build(l,mid,LNode);
    build(mid+1,r,RNode);
    sum[x]=sum[LNode]+sum[RNode];
    //build(1,n,1);//從根開始向上建立線段樹
}
///區間最小值個數
/*void update(int x){//區間最小值的個數
    Min[x]=min(Min[LNode],Min[RNode]);
    if(Min[LNode]==Min[RNode]){
        Min[x]=Min[LNode];
        cnt[x]=cnt[LNode]+cnt[RNode];
    }else if(Min[LNode]<Min[RNode]){
        Min[x]=Min[LNode];
        cnt[x]=cnt[LNode];
    }else{
        Min[x]=Min[RNode];
        cnt[x]=cnt[RNode];
    }
}*/

void down(int l,int r,int x){//标記下傳函數(延遲修改技術)
    int mid=l+(r-l)/2;
    if(tag[x]>0){//tag[x]!=0 區間加上某個數
        ///區間加上某個數
        //tag[LNode]+=tag[x];
        //tag[RNode]+=tag[x];
        ///區間加上某個數
        //sum[LNode]+=(mid-l+1)*tag[x];
        //sum[RNode]+=(r-mid)*tag[x];
        tag[LNode]=tag[RNode]=tag[x];
        sum[LNode]=(mid-l+1)*tag[x];
        sum[RNode]=(r-mid)*tag[x];
        tag[x]=0;
        ///區間最小值(區間最小值個數)
        //Min[LNode]+=tag[x];
        //Min[RNode]+=tag[x];
    }
}
///區間最小值個數查詢
/*P query1(int A,int B,int l,int r,int x){
    if(A<=l&&B>=r) return P(Min[x],cnt[x]);//min和cnt都取出來
    down(l,r,x);
    int mid=l+(r-l)/2;
    P ans=P(inf,0);
    if(A<=mid) ans=min(ans,query1(A,B,l,mid,LNode));
    if(B>mid){
        P temp=min(ans,query1(A,B,mid+1,r,RNode));
        if(temp.first==ans.first) ans.second+=temp.second;
        else if(temp.first<ans.first) ans=temp;
    }
    return ans;
}*/

//線段樹查詢(自頂向下)
int query(int A,int B,int l,int r,int x){///區間查詢和(log(n)))
    if(A<=l&&B>=r) return sum[x];
    down(l,r,x);//查詢之前,檢查是否要下傳标記
    //(延遲修改技術,子節點不一定是正确的,但是目前結點一定是正确的)
    int mid=l+(r-l)/2,ans=0;
    ///維護區間最小值
    //int ans=0x3f3f3f3f
    //if(A<=mid) ans=min(ans,query(A,B,l,mid,LNode));
    //if(A<=mid) ans=min(ans,query(A,B,mid+1,r,RNode));
    if(A<=mid) ans+=query(A,B,l,mid,LNode);//查詢左子樹
    if(B>mid) ans+=query(A,B,mid+1,r,RNode);//查詢右子樹
    return ans;
}

//[A,B]:修改為v,[l,r]:目前結點對應的區間,x:目前結點
void change(int A,int B,int v,int l,int r,int x){///區間修改資料(log(n))
    if(A<=l&&B>=r) {
        tag[x]=v;
        sum[x]=v*(r-l+1);
        ///區間加上某個數
        //tag[x]+=v;
        //sum[x]+=v*(r-l+1);
        //Min[x]+=v;
        return ;
    }
    down(l,r,x);//修改之前,檢查是否需要下傳标記
    int mid=l+(r-l)/2;
    if(A<=mid) change(A,B,v,l,mid,LNode);
    if(B>mid) change(A,B,v,mid+1,r,RNode);
    sum[x]=sum[LNode]+sum[RNode];
    ///區間最小值
    //Min[x]=min(Min[LNode],Min[RNode]);
    ///區間最小值個數
    //update(x);
}

int main(){
    int T,Case=0;
    scanf("%d",&T);
    while(T--){
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n*4;i++) tag[i]=0;///多組輸出tag數組清零
        for(int i=1;i<=n;i++) a[i]=1;
        build(1,n,1);
        while(m--){
            int l,r,v;
            scanf("%d%d%d",&l,&r,&v);
            change(l,r,v,1,n,1);
            //cout<<query(1,n,1,n,1);
        }
        printf("Case %d: The total value of the hook is %d.\n",++Case,query(1,n,1,n,1));
    }
    return 0;
}