編者注:本文采用梯度下降法來求解的logistic回歸,關于其思想以及程式設計原理見本人之前文章《梯度下降法求解線性回歸的python實作及其結果可視化》(https://zhuanlan.zhihu.com/p/30562194),在這裡不再贅述。
01 非線性決策邊界的logistic回歸拟合
正常的logistic回歸在解決分類問題時,通常是用于線性決策邊界的分類(如下圖-左圖),因為logistic回歸可以視為線性回歸的一種轉化,其回歸模型為 (sigmoid函數):
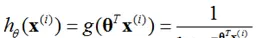
image.png
式中的z=θTx(i)就是不同x的線性表達式f(x) = g(w0+w1x1+w2x2)。那麼,對于線性決策邊界的分類,如何用logistic回歸預測、拟合呢?這時候就需要将f(x) = g(w0+w1x1+w2x2)的線性函數式轉化成多項式:f(x) = g(w0+w1x1+w2x2+w3x12+w4x22+w5x1x2)去拟合(如下圖-中圖)。
image.png
但是,這種處理方式相比較于線性函數表達式會産生很多的項數,因而其變量(特征)也比較多,如果我們沒有足夠的資料集(訓練集)去限制這個變量過多的模型,那麼就會發生過拟合。如上圖中的最右邊圖形,其分類結果完全正确,但這個分類模型似乎太過完美了吧?連交叉部分的類别也劃分出來了。過拟合就是表示它的分類隻是适合于自己這個測試用例,對需要分類的真實樣本(例如測試集)而言,特别是針對新的資料樣本,實用性反倒可能會低很多。
02 正則化優化logistic回歸過拟合
正則化(Regularized)是解決過拟合問題的一種方法,它将保留所有的特征變量,但是會減小特征變量的數量級(參數數值的大小θ(j)),當我們有很多特征變量時,其中每一個變量都能對預測産生一點影響,每一個變量都是有用的,是以我們不希望把它們删掉,但是我們可以通過正則化方式增加它們的成本cost,來減小我們的函數中的一些項的權重,其意義在于平滑函數曲線,使得預測函數相對簡單一些,避免過度複雜函數的過拟合問題。
其處理方法為:對某些θ(j)加入懲罰項:
image.png
在這裡λ稱作正則化參數,它通過平衡拟合訓練的目标和保持參數值較小的目标。進而來保持假設的形式相對簡單,來避免過度的拟合。
三、Regularized Logistic Regression執行個體
(1)假設有這樣一個非線性決策邊界的分類資料,(資料來自
https://github.com/jdwittenauer/ipython-notebooks/tree/master/data 中的ex2data2.txt):
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'D:\python\ml data\ex2data2.txt' #路徑要設定為你自己的路徑
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
data2.head()
image.png
(2)其資料可視化為:
positive = data2[data2['Accepted'].isin([1])] #Accepted列中的1設定為positive
negative = data2[data2['Accepted'].isin([0])] #Accepted列中的0設定為positive
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()
image.png
(3)建構多項式特征值
上圖的可視化結果可以看到該資料類别是明顯的非線性決策邊界,對此我們首先建構變量'Test 1', 'Test 2'的多項式特征值,如下:
degree = 5
x1 = data2['Test 1']
x2 = data2['Test 2']
data2.insert(3, 'Ones', 1)
for i in range(1, degree):
for j in range(0, i):
data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)
data2.drop('Test 1', axis=1, inplace=True) #删除Text1列并進行替換
data2.drop('Test 2', axis=1, inplace=True) #删除Text2列并進行替換
data2.head()
image.png
其中degree表示多項式的幂數,range(1, degree)表示了從1次到4次,即由data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)指令可知,每一列列名的F第一個數代表了x1的幂值,第二個數代表了x2的幂值,如F31則表示x13x2,以此類推。
(4)建構加入懲罰項的cost函數
def sigmoid(z):
return 1 / (1 + np.exp(-z)) #建構sigmoid函數
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
reg = (learningRate / 2 * len(X)) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
return np.sum(first - second) / (len(X)) + reg
reg就是懲罰項,建構思路參考正則化優化logistic回歸過拟合部分的懲罰項設定規則。
(5)采用梯度下降法求解
def gradientReg(theta, X, y, learningRate):
theta = np.matrix(theta) #轉化為矩陣
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1]) #計算參數theta的個數
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i]) #兩矩陣相乘
if (i == 0):
grad[i] = np.sum(term) / len(X) #一般來說第一個參數不需要正則化
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
return grad
具體的梯度下降法思路可以參考之前本人寫的關于梯度下降法求解線性回歸的文章,隻是在這裡加了一個懲罰項的梯度下降求解,其構造思路如下圖所示。
image.png
(6)将變量代入進行拟合
基于表格資料建構x、y變量并轉化成數組,這部分内容可以參考之前本人寫的關于梯度下降法求解線性回歸的文章。然後用梯度下降法函數求解并計算cost。
# set X and y (remember from above that we moved the label to column 0)
cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]
# convert to numpy arrays and initalize the parameter array theta
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(11)
learningRate = 1 #設定學習率
gradientReg(theta2, X2, y2, learningRate)
costReg(theta2, X2, y2, learningRate)
得到的cost值為0.6931471805599454。
值得注意的是,在這裡我們并沒有在這個函數中執行梯度下降,而是基于梯度下降計算結果加入梯度項來實作的一個漸變步驟,是以,在這裡我們還可以調用octave的内建函數fminunc();來獲得最優的theta和最小的cost。在Python,我們可以使用SciPy的優化API來完成。
import scipy.optimize as opt
result2 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))
result2
(7)計算預測結果精度
def predict(theta, X):
probability = sigmoid(X * theta.T)
return [1 if x >= 0.5 else 0 for x in probability]
theta_min = np.matrix(result2[0])
predictions = predict(theta_min, X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) % len(correct))
print 'accuracy = {0}%'.format(accuracy)
首先建構預測值函數,然後将該值與原始類别值0,1比較,計算其正确的精度,結果為91%。
寫作不易,特别是技術類的寫作,請大家多多支援,關注、點贊、轉發等等..
參考文獻: