給定 n 個非負整數,用來表示柱狀圖中各個柱子的高度。每個柱子彼此相鄰,且寬度為 1 。
求在該柱狀圖中,能夠勾勒出來的矩形的最大面積。
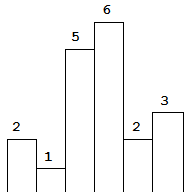
以上是柱狀圖的示例,其中每個柱子的寬度為 1,給定的高度為
[2,1,5,6,2,3]
。
圖中陰影部分為所能勾勒出的最大矩形面積,其面積為
10
個機關。
示例:
輸入: heights = [2,1,5,6,2,3]
輸出: 10
暴力解法: 假設正确結果中包含heights[0],則計算以heights[0]為開始的最大面積。後面以此類推,最終将以2,1,5,6,2,3為開始的最大面積比較,得出最大值
思想: 最大矩陣面積必定是以2,1,5,6,2,3其中一個為開頭的, 我隻要固定矩陣的開始位置,比較不同開始位置的最大值即可。
結果: 逾時
class Solution:
def largestRectangleArea(self, heights):
"""
:type heights: List[int]
:rtype: int
"""
l = len(heights)
max_area = 0
for i in range(l):
height_min = 100000000000
for j in range(i, l):
height_min = min(height_min, heights[j])
max_area = max(max_area, height_min*(j-i+1))
return max_area
優化一:
矩陣的最大面積必定是以2,1,5,6,2,3其中一個為高的,
我隻要比較以2為高的最大矩陣面積,
以1為高的最大矩陣面積,
以5為高的最大矩陣面積,
以6為高的最大矩陣面積,
以2為高的最大矩陣面積,
以3為高的最大矩陣面積
即可。 轉換思想,暴力方法固定開始位置的思想,現在是固定高度。
設立left和right清單。 left[i] = k表示:
heights[k] < heights[i] ,
j = k+1,...., i 滿足 heights[j] >= heights[i]
以heights = [2,1,5,6,2,3]
left = [-1,-1,1,2,1,4]
right =[1,6,4,4,6,6]
最後在周遊一遍heights
class Solution:
def largestRectangleArea(self, heights):
"""
:type heights: List[int]
:rtype: int
"""
# 優化過的
l = len(heights)
if l == 0:
return 0
if l == 1:
return heights[0] * 1
left = [0] * len(heights)
right = [0] * len(heights)
left[0] = -1
for i in range(1, l):
if heights[i] > heights[i-1]:
left[i] = i - 1
else:
# 優化的地方
j = left[i-1]
tmp = heights[i]
while (j >= 0 and heights[j] >= tmp) or j == -1:
if j == -1:
left[i] = -1
break
j = j - 1
left[i] = j
right[l-1] = l
max_area = 0
for i in range(l-2, -1,-1):
if heights[i] > heights[i+1]:
right[i] = i + 1
else:
j = right[i+1]
tmp = heights[i]
while (j <= l-1 and heights[j] >= tmp) or j == l:
if j == l:
right[i] = l
break
j = j + 1
right[i] = j
max_area = max(max_area, (right[i]-left[i]-1)*heights[i])
max_area = max(max_area, (right[l-1]-left[l-1]-1)*heights[l-1])
return max_area
方法三: 遞增棧
目前不了解
class Solution:
def largestRectangleArea(self, heights):
"""
:type heights: List[int]
:rtype: int
"""
heights.append(0)
st, mx = [], 0
for i in range(len(heights)):
while st and heights[st[-1]] >= heights[i]:
c = st.pop()
mx = max(mx, heights[c]*(i-st[-1]-1 if st else i))
st.append(i)
return mx