knuth的SJT實作

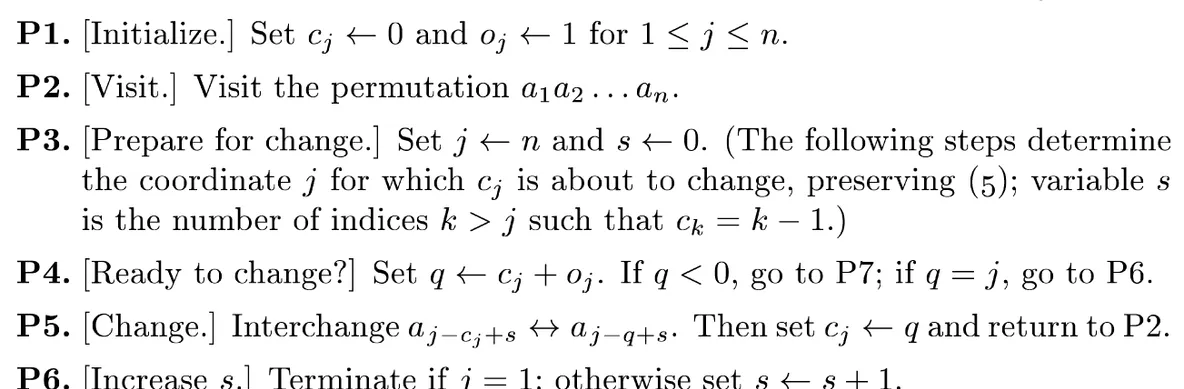
思路

SJT算法就是給每個值一個方向，初始都向左（P1），然後從最大的值開始檢查（P3），一直檢查到最小的值，直到找到值，使得其方向上的下一個值小于它（P4），然後将其往那邊移動一步（P5），然後繼續從最大的值開始找（return to P2）。對于每個被檢查的值，如果這個值的方向上的下一個值不小于它，就調轉它的方向，然後繼續檢查次小的值。

這樣為什麼可以枚舉到所有的排列呢？這實際上可以遞歸的證明。首先我們知道，n=1時，這樣是可以做到枚舉到所有排列的。然後我們假設對于n=N-1時，這樣做可以做到枚舉到所有的排列。然後我們要證明對于n=N時，這樣做可以枚舉到所有的排列。

首先，将N移動到最左邊或者最右邊之後，我們将1到(N-1)的子序列變換到下一個全排列，在算法中展現為繼續檢查次小值能不能移動。由假設可知，通過這種方式，子序列可以周遊到所有的全排列，是以我們隻需要将N反向再穿插過去，就可以周遊到包含這個子序列的1到N的全排列了。

P1

到是序列，是的右邊小于的數的個數，是的方向，1表示向左，-1表示向右。剛開始，序列是，是以把都初始化為0，都初始化為1。

P2

不知道幹啥的

P3

然後我們標明選擇要移動的數字，一開始找最大的數字，也就是令。令表示的左邊比大的數字的個數，那麼的下标就是，可以形象地了解為，從的左邊拿掉比小的個數字，然後再将個比大的數字插入到的左邊。

P4

因為我們的思路是先讓大的走，而且不允許小的值把大的“擠走”，是以既然我們現在是要讓走，說明大于的都走不動了，也就是說，比大的值中，向右走的必然全部集中在最右邊，向左走的必然全部集中在最左邊。是以，走的那個方向上如果有小于的值，那麼該方向上的下一個值必然是小于的。

我們令，如果能走得動的話，這個實際上就是的新值。

如果，說明在向右走，且右邊沒有比它小的值了，也就是說走不動了。這時就跳轉到P7，改變的方向，然後令，即繼續檢查下一個值能不能走得動。