台灣國立大學（林軒田）《機器學習基石》（第9-10講）Linear Regression and Logistic Regression

課程位址：https://class.coursera.org/ntumlone-001/class

課件講義：http://download.csdn.net/download/malele4th/10208897

注明：文中圖檔來自《機器學習基石》課程和部分部落格

建議：建議讀者學習林軒田老師原課程，本文對原課程有自己的改動和了解

目錄

• 目錄
  • Lecture 9 Linear Regression
    • 線性回歸問題
    • 線性回歸算法
    • 泛化問題
    • 總結
  • Lecture 10 Logistic Regression
    • 邏輯回歸問題
    • 邏輯回歸 error
    • 梯度下降
    • 總結

Lecture 9 Linear Regression

上節課，我們主要介紹了在有noise的情況下，VC Bound理論仍然是成立的。同時，介紹了不同的error measure方法。本節課介紹機器學習最常見的一種算法：Linear Regression.

線性回歸問題

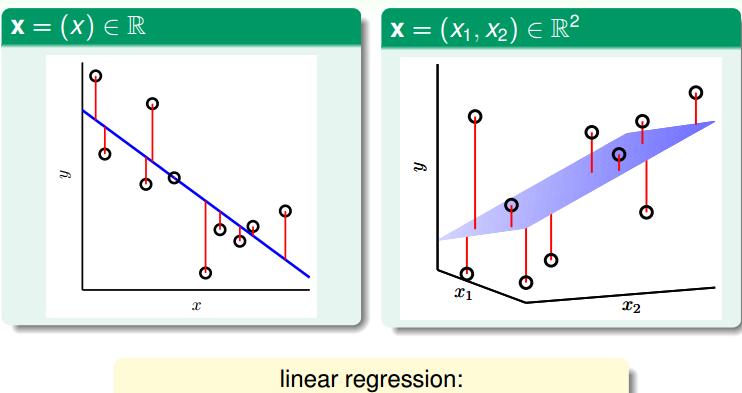
根據上圖，在一維或者多元空間裡，線性回歸的目标是找到一條直線（對應一維）、一個平面（對應二維）或者更高維的超平面，使樣本集中的點更接近它，也就是殘留誤差Residuals最小化。

一般最常用的錯誤測量方式是基于最小二乘法，其目标是計算誤差的最小平方和對應的權重w，即上節課介紹的squared error

這裡提一點，最小二乘法可以解決線性問題和非線性問題。線性最小二乘法的解是closed-form，即 X=(ATA)−1ATy ，而非線性最小二乘法沒有closed-form，通常用疊代法求解。本節課的解就是closed-form的

線性回歸算法

樣本資料誤差Ein是權重w的函數，因為X和y都是已知的。我們的目标就是找出合适的w，使Ein能夠最小。那麼如何計算呢？

首先，運用矩陣轉換的思想，将Ein計算轉換為矩陣的形式。

兩種解法：

偏導為0

梯度下降

對于此類線性回歸問題，Ein(w)一般是個凸函數。凸函數的話，我們隻要找到一階導數等于零的位置，就找到了最優解。那麼，我們将Ew對每個wi,i=0,1,⋯,d求偏導，偏導為零的wi，即為最優化的權重值分布。

最終，我們推導得到了權重向量 w=(XTX)−1XTy ，這是上文提到的closed-form解。其中， (XTX)−1XT 又稱為僞逆矩陣pseudo-inverse，記為 X+ ，次元是(d+1)xN。

但是，我們注意到，僞逆矩陣中有逆矩陣的計算，逆矩陣 (XTX)−1 是否一定存在？一般情況下，隻要滿足樣本數量N遠大于樣本特征次元d+1，就能保證矩陣的逆是存在的，稱之為非奇異矩陣。但是如果是奇異矩陣，不可逆怎麼辦呢？其實，大部分的計算逆矩陣的軟體程式，都可以處理這個問題，也會計算出一個逆矩陣。是以，一般僞逆矩陣是可解的。

泛化問題

現在，可能有這樣一個疑問，就是這種求解權重向量的方法是機器學習嗎？或者說這種方法滿足我們之前推導VC Bound，即是否泛化能力強Ein≈Eout？

有兩種觀點：

1、這不屬于機器學習範疇。因為這種closed-form解的形式跟一般的機器學習算法不一樣，而且在計算最小化誤差的過程中沒有用到疊代。

2、這屬于機器學習範疇。因為從結果上看，Ein和Eout都實作了最小化，而且實際上在計算逆矩陣的過程中，也用到了疊代。

學習曲線：

當N足夠大時，Ein與Eout逐漸接近，滿足Ein≈Eout，且數值保持在noise level。這就類似VC理論，證明了當N足夠大的時候，這種線性最小二乘法是可以進行機器學習的，算法有效！

總結

本節課，我們主要介紹了Linear Regression。首先，我們從問題出發，想要找到一條直線拟合實際資料值；然後，我們利用最小二乘法，用解析形式推導了權重w的closed-form解；接着，用圖形的形式得到 Eout−Ein≈2(N+1)N ，證明了linear regression是可以進行機器學習的，；最後，我們證明linear regressin這種方法可以用在binary classification上，雖然上界變寬松了，但是仍然能得到不錯的學習方法。

Lecture 10 Logistic Regression

上一節課，我們介紹了Linear Regression線性回歸，以及用平方錯誤來尋找最佳的權重向量w，獲得最好的線性預測。本節課将介紹Logistic Regression邏輯回歸問題。

邏輯回歸問題

一個心髒病預測的問題：根據患者的年齡、血壓、體重等資訊，來預測患者是否會有心髒病。很明顯這是一個二分類問題，其輸出y隻有{-1,1}兩種情況。

二進制分類，一般情況下，理想的目标函數f(x)>0.5，則判斷為正類1；若f(x)<0.5，則判斷為負類-1。

但是，如果我們想知道的不是患者有沒有心髒病，而是到底患者有多大的幾率是心髒病。這表示，我們更關心的是目标函數的值（分布在0,1之間），表示是正類的機率（正類表示是心髒病）。這跟我們原來讨論的二分類問題不太一樣，我們把這個問題稱為軟性二分類問題（’soft’ binary classification）。這個值越接近1，表示正類的可能性越大；越接近0，表示負類的可能性越大。

邏輯回歸 error

現在我們将Logistic Regression與之前講的Linear Classification、Linear Regression做個比較：

這三個線性模型都會用到線性scoring function s=wTx 。linear classification的誤差使用的是0/1 err；linear regression的誤差使用的是squared err。那麼logistic regression的誤差該如何定義呢？

我們得到logistic regression的err function，稱之為cross-entropy error交叉熵誤差：

梯度下降

下面讨論一下η的大小對疊代優化的影響：η如果太小的話，那麼下降的速度就會很慢；η如果太大的話，那麼之前利用Taylor展開的方法就不準了，造成下降很不穩定，甚至會上升。是以，η應該選擇合适的值，一種方法是在梯度較小的時候，選擇小的η，梯度較大的時候，選擇大的η，即η正比于 ||∇Ein(wt)|| 。這樣保證了能夠快速、穩定地得到最小值Ein(w)。

總結

我們今天介紹了Logistic Regression。首先，從邏輯回歸的問題出發，将P(+1|x)作為目标函數，将 θ(wTx) 作為hypothesis。接着，我們定義了logistic regression的err function，稱之為cross-entropy error交叉熵誤差。然後，我們計算logistic regression error的梯度，最後，通過梯度下降算法，計算 ∇Ein(wt)≈0 時對應的wt值。