自己整理的哈，有錯誤還請各位大哥指正！
1.什麼是O
O表示算法複雜度 ，他需要通過時間複雜度和空間複雜度來描述。
①時間複雜度:一個語句的頻度即該語句被執行的次數，程式中所有語句的頻度之和記為T(n)，時間複雜度就是T(n)的數量級函數，其中n表示問題的規模。
如常見的冒泡排序最壞時間複雜度為O(n^2)，即初始資料為逆序排序。
②空間複雜度:算法所耗費的存儲空間，也是問題規模n的函數。
若算法所需輔助空間為常量，則空間複雜度是O(1)，即原地工作。
2.資料結構三要素
①邏輯結構：指資料之間的邏輯關系，與存儲關系無關。主要有集合；線性（一對一）；樹形（一對多）；圖（多對多）四類。
②存儲結構：指資料在計算機中的表示。隻要有順序存儲；鍊式存儲；索引存儲；散列存儲。
③資料的運算：施加在資料上的運算。
3.循環與遞歸
遞歸優點：代碼簡潔清晰
缺點：每遞歸一層,就會在記憶體生成一個棧儲存遞歸的資訊，如果遞歸深度過深,有棧溢出的問題。循環則不會有這樣的問題。
循環優點：結構簡單易實作
缺點：沒有遞歸簡介明了（我認為所有遞歸都可以寫成循環，但比較麻煩）
4.貪心，dp及分治的差別
貪心：隻考慮目前最優解，而非全局最優。
dp：考慮到全局最優，求解子問題過程中保留可能的局部最優解，從下往上，一步步對比出全局最優解。
分治：顧名思義分而治之，将問題分為若幹規模小且與原問題相似的子問題，遞歸解決再合并結果。如歸并排序。
5.順序表和連結清單：
空間上：順序表需要連續存儲空間
記憶體上：連結清單有指針額外占用空間
随機存取上：順序表支援
插入删除上：連結清單隻需修改指針，而順序表需大量移動元素
6.頭指針和頭節點：
頭指針：不管有沒有頭節點，永遠指向連結清單第一個節點。作用：具有辨別作用。
頭節點：帶頭節點連結清單中的第一個節點，通常不存儲資訊。作用：使得第一個節點和其他節點的操作統一；使得空表和非空表操作統一。
7.棧和隊列：
棧：先進後出，隻能在一端進行插入删除。
隊列：先進先出，隻能在一端插入另一端删除。
相同點：都可鍊式順序存儲，都是操作受限的線性表。
8.共享棧：
兩個順序棧共享一個一維數組空間，棧底分别設在兩端，插入資料時向中間延申，是以隻有空間被占滿時才上溢。
9.判斷循環隊列的空滿：
一般犧牲一個單元格：當(隊尾+1）%maxnum=隊頭時則為隊滿；當隊頭=隊尾時則為隊空。
也可以增設一個資料成員表示隊内元素個數來判斷：個數=0隊空，個數=maxnum為隊滿。
10.kmp算法中next數組的計算：
當第j個字元比對失敗時，記1~j-1的字元串為S；則next【j】=S的模式串最長相等前字尾長度+1，特别地next【1】=0。
改進後的nextvel數組：記next【j】的值為x，當模式串下标為x的字元=目前模式串所指字元，說明就算移動也會比對失敗，是以直接nextvel【j】=nextvel【x】（即參考前面的相同字元的nextval值。
11.線索二叉樹：
作用：使得不用周遊的情況下直接找到某結點的前驅或後繼。
先序線索化不能直接找前驅，後序線索化不能直接找後繼
12.二叉排序樹
空樹或：左子樹結點的值小于他，右子樹結點的值大于他，且左右都是二叉排序樹。
13.平衡二叉樹
空樹或：左右子樹高度差絕對值不超過1且左右都是平衡二叉樹。
14.哈夫曼樹
帶權路徑最小的樹，也稱為最優二叉樹
14.樹的存儲結構
順序存儲和鍊式存儲（一般二叉樹才有可能用順序存儲）
三種方法：雙親表示法（存該結點的父親），孩子表示法（鍊式存儲該節點的所有孩子），孩子兄弟表示法（左邊存孩子右邊存兄弟）
15.B樹(多路平衡查找樹)m階B樹的結點最多m個子樹
要求根的子樹個數為【2，m】，關鍵字數=【1，m-1】；非根的子樹為【m/2，m】；關鍵字數=【(m/2)-1，m-1】
查找：同二叉排序樹(大了往右，小了往左)，隻不過不是兩路分支而是多路分支
插入：同二叉排序樹一樣找到位置插入，然後不滿足B樹條件時進行不斷分裂(中間位置的關鍵字去父節點中，左邊的關鍵字不動，右邊的關鍵字新生成一個結點)
删除：①直接删：删除後仍滿足B樹條件。
②兄弟夠借：父子互換法，兄弟頂替被删的關鍵字且父子互換。
③兄弟不夠借：父親下墜法，父親下來與兄弟合并。
16.B樹和B+樹差別：
B+樹是應資料庫所需而出現的一種B樹的變形。
B+樹結點的子樹個數=關鍵字個數。而B樹子樹個數-1=關鍵字個數。
B+樹僅在葉子節點存儲索引對應資訊（而B樹則每個節點中都存放了索引對應資訊），是以一個磁盤可以存下更多的索引元素，大大減少磁盤通路操作。這也是為什麼大多數資料庫選擇B+樹的主要原因。
B+樹葉子節點間有雙向的指針，支援順序查找、範圍查找。
17.資料庫為什麼用B+樹不用B樹：因為查詢操作需要讀磁盤，而磁盤是慢速裝置，是以當然是讀的次數越少越好，也就是樹的高度越小越好。而B+樹相對B樹而言，它的非葉子節點不存儲關鍵字對應資訊，隻存儲關鍵字，是以規定的磁盤空間就能存放更多關鍵字，樹也越矮，查找速度更快。且葉子節點有雙向的指針，支援順序查找、範圍查找。
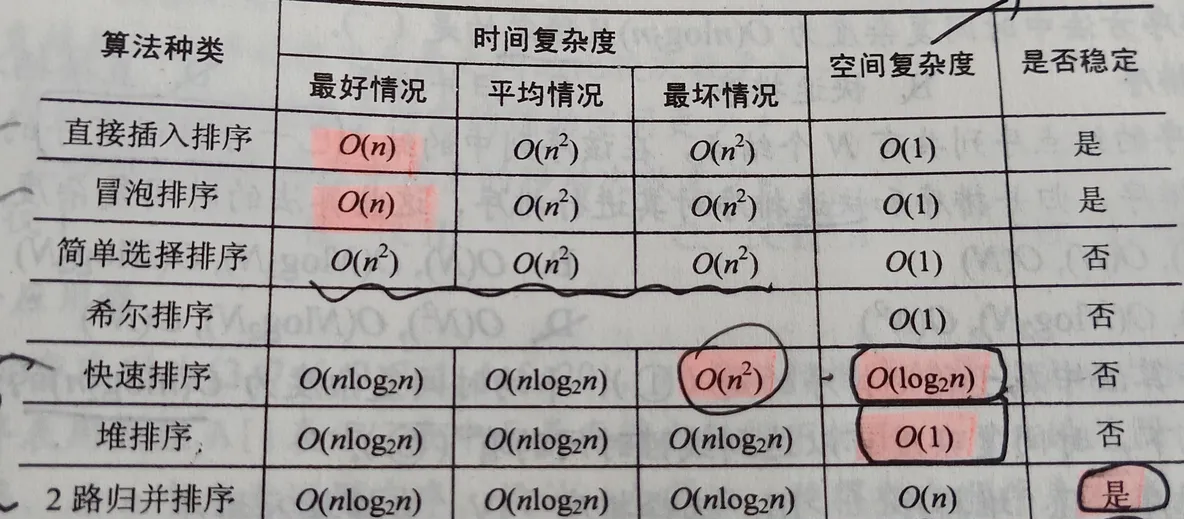
18.排序
d是關鍵字數，r時隊列數，n是待排序數。
19.快排複雜度怎麼來的：
最好為O（nlogn）。每次需要将數組分成兩半進行比較交換，最好情況下每次都分為等長兩個部分，則需要logn次劃分。最差情況下分為n-1個元素和0個元素，則需n次劃分。
不管最好還是最差劃分 每趟排序都需要對元素進行n次比較，是以最好為nlogn，最差為n^2。
改進：每次随機選擇基準元素可以使得最壞情況幾乎不會發生。
20.基數排序：
将所有待比較數統一為同樣的長度，不足的前面補零 。然後對每個數的第i位數進行比較，插入相應的隊列，最後将隊列用指針連結。如此循環直到最高位比較完畢。
時間複雜度為d（n+r），其中d為關鍵字個數。r為隊列數，n為排序數。
![hiho1063(樹型dp)[圖]](data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=)