單源最短路徑

在最短路徑問題中，我們給定一個帶權重的有向圖和權重函數, 該權重函數将每條邊映射到實數值的權重上。圖中一條路徑的權重是構成該路徑的所有邊的權重之和：

定義從結點u到結點v的最短路徑權重如下：

從結點u到結點v的最短路徑則定義為任何一條權重為的從u到v的路徑p。

最短路徑的幾個變體

單源最短路徑：給定一個圖G=(V,E),我們希望找到從給定源結點到每個節點的最短路徑。

單目的地最短路徑問題：找到從每個節點u到給定目的地節點t的最短路徑。如果将圖的每條邊的方向翻轉過來，我們就可以将這個問題轉換為單源最短路徑問題。

單節點對最短路徑問題：找到從給定節點u到給定節點v的最短路徑。如果解決了針對單個節點u的單源最短路徑問題，那麼也就解決這個問題。

所有節點對最短路徑問題：對于每個節點u和v，找到從結點u到結點v的最短路徑。雖然可以針對每節點運作一遍單源最短路徑算法，但通常可以更快地解決這個問題。

初始化

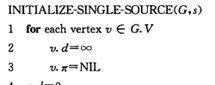
松弛操作

Bellman-Ford算法

topo sort

有向無環圖中的單源最短路徑問題

根據節點的拓撲排序次序對帶權重的有向無環圖G=(V,E)進行邊的松弛操作，我們便可以在時間内計算出從單個源結點到所有節點之間的最短路徑。在有向無環圖中，即使存在權重為負的邊，但因為沒有權重為負的環路，最短路徑都是存在的。

    算法首先對有向無環圖進行拓撲排序，以便确定結點之間的一個線性次序。以便确定結點之間的一個線性次序。如果有向無環圖包含從結點u到結點v的一條路徑，則u的拓撲排序的次序中位于結點v的前面。我們隻需要按照拓撲排序的次序對結點進行一遍處理即可。每次對一個節點進行處理時，我們對從該節點發出的發出的所有的邊進行松弛操作。

Dijkstra算法

三個算法的對比

所有節點對的最短路徑問題

Floyd-Warshall算法

//基本思想是：

//進行中轉......允許經過1~n号所有頂點進行中轉，求任意兩點之間的最短路程。

//用一句話概括就是：從i号頂點到j号頂點隻經過前k号點的最短路程。其實這是一種"動态規劃"的思想。