文章目錄
- 紅黑樹的概念
- 紅黑樹的性質
- 紅黑樹結點的定義
- 紅黑樹的插入
- 紅黑樹的驗證
- 紅黑樹的查找
- 紅黑樹的删除
- 紅黑樹與AVL樹的比較
紅黑樹的概念
紅黑樹是一種二叉搜尋樹,但在每個結點上增加了一個存儲位用于表示結點的顔色,這個顔色可以是紅色的,也可以是黑色的,是以我們稱之為紅黑樹。
紅黑樹通過對任何一條從根到葉子的路徑上各個結點着色方式的限制,確定沒有一條路徑會比其他路徑長出兩倍,是以紅黑樹是近似平衡的。
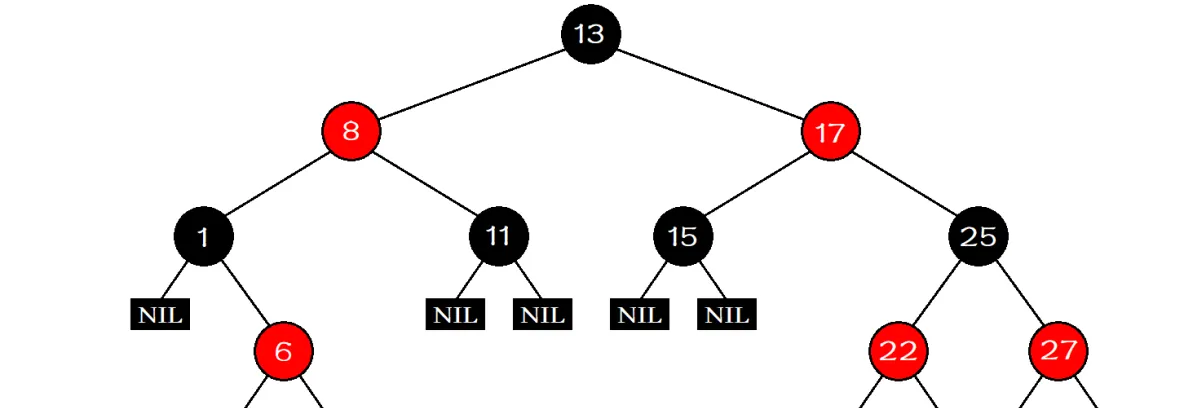
紅黑樹的性質
紅黑樹有以下五點性質:
- 每個結點不是紅色就是黑色。
- 根結點是黑色的。
- 如果一個結點是紅色的,則它的兩個孩子結點是黑色的。
- 對于每個結點,從該結點到其所有後代葉子結點的簡單路徑上,均包含相同數目的黑色結點。
- 每個葉子結點都是黑色的(此處的葉子結點指定是空結點)。
紅黑樹如何確定從根到葉子的最長可能路徑不會超過最短可能路徑的兩倍?
根據紅黑樹的性質3可以得出,紅黑樹當中不會出現連續的紅色結點,而根據性質4又可以得出,從某一結點到其後代葉子結點的所有路徑上包含的黑色結點的數目是相同的。
我們假設在紅黑樹中,從根到葉子的所有路徑上包含的黑色結點的個數都是個,那麼最短路徑就是全部由黑色結點構成的路徑,即長度為。
而最長可能路徑就是由一黑一紅結點構成的路徑,該路徑當中黑色結點與紅色結點的數目相同,即長度為。
是以,紅黑樹從根到葉子的最長可能路徑不會超過最短可能路徑的兩倍。
紅黑樹結點的定義
我們這裡直接實作KV模型的紅黑樹,為了友善後序的旋轉操作,将紅黑樹的結點定義為三叉鍊結構,除此之外還新加入了一個成員變量,用于表示結點的顔色。
template<class K, class V>
struct RBTreeNode
{
//三叉鍊
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
//存儲的鍵值對
pair<K, V> _kv;
//結點的顔色
int _col; //紅/黑
//構造函數
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col(RED)
{}
}; 在這裡我們可以使用枚舉來定義結點的顔色,這樣可以增加代碼的可讀性和可維護性,并且便于後序的調試操作。
//枚舉定義結點的顔色
enum Colour
{
RED,
BLACK
}; 為什麼構造結點時,預設将結點的顔色設定為紅色?
當我們向紅黑樹插入結點時,若我們插入的是黑色結點,那麼插入路徑上黑色結點的數目就比其他路徑上黑色結點的數目多了一個,即破壞了紅黑樹的性質4,此時我們就需要對紅黑樹進行調整。
若我們插入紅黑樹的結點是紅色的,此時如果其父結點也是紅色的,那麼表明出現了連續的紅色結點,即破壞了紅黑樹的性質3,此時我們需要對紅黑樹進行調整;但如果其父結點是黑色的,那我們就無需對紅黑樹進行調整,插入後仍滿足紅黑樹的要求。
總結一下:
- 插入黑色結點,一定破壞紅黑樹的性質4,必須對紅黑樹進行調整。
- 插入紅色結點,可能破壞紅黑樹的性質3,可能對紅黑樹進行調整。
權衡利弊後,我們在構造結點進行插入時,預設将結點的顔色設定為紅色。
紅黑樹的插入
紅黑樹插入結點的邏輯分為三步:
- 按二叉搜尋樹的插入方法,找到待插入位置。
- 将待插入結點插入到樹中。
- 若插入結點的父結點是紅色的,則需要對紅黑樹進行調整。
其中前兩步與二叉搜尋樹插入結點時的邏輯相同,紅黑樹的關鍵在于第三步對紅黑樹的調整。
紅黑樹在插入結點後是如何調整的?
實際上,在插入結點後并不是一定會對紅黑樹進行調整,若插入結點的父結點是黑色的,那麼我們就不用對紅黑樹進行調整,因為本次結點的插入并沒有破壞紅黑樹的五點性質。
隻有當插入結點的父結點是紅色時才需要對紅黑樹進行調整,因為我們預設插入的結點就是紅色的,如果插入結點的父結點也是紅色的,那麼此時就出現了連續的紅色結點,是以需要對紅黑樹進行調整。
因為插入結點的父結點是紅色的,說明父結點不是根結點(根結點是黑色的),是以插入結點的祖父結點(父結點的父結點)就一定存在。
紅黑樹調整時具體應該如何調整,主要是看插入結點的叔叔(插入結點的父結點的兄弟結點),根據插入結點叔叔的不同,可将紅黑樹的調整分為三種情況。
情況一:插入結點的叔叔存在,且叔叔的顔色是紅色。
此時為了避免出現連續的紅色結點,我們可以将父結點變黑,但為了保持每條路徑黑色結點的數目不變,是以我們還需要将祖父結點變紅,再将叔叔變黑。這樣一來既保持了每條路徑黑色結點的數目不變,也解決了連續紅色結點的問題。
但調整還沒有結束,因為此時祖父結點變成了紅色,如果祖父結點是根結點,那我們直接再将祖父結點變成黑色即可,此時相當于每條路徑黑色結點的數目都增加了一個。
但如果祖父結點不是根結點的話,我們就需要将祖父結點當作新插入的結點,再判斷其父結點是否為紅色,若其父結點也是紅色,那麼又需要根據其叔叔的不同,進而進行不同的調整操作。
是以,情況一的抽象圖表示如下:
注意: 叔叔存在且為紅時,cur結點是parent的左孩子還是右孩子,調整方法都是一樣的。
情況二:插入結點的叔叔存在,且叔叔的顔色是黑色。
這種情況一定是在情況一繼續往上調整的過程中出現的,即這種情況下的cur結點一定不是新插入的結點,而是上一次情況一調整過程中的祖父結點,如下圖:
我們将路徑中祖父結點之上黑色結點的數目設為,将叔叔結點之下黑色結點的數目設為,則在插入結點前,圖示兩條路徑黑色結點的數目分别為 和 ,很明顯 是一定大于 的,是以在插入結點前就不滿足紅黑樹的要求了,是以說叔叔結點存在且為黑這種情況,一定是由情況一往上調整過程中才會出現的一種情況。
需要注意:
- 從根結點一直走到空位置就算一條路徑,而不是從根結點走到左右結點均為空的葉子結點時才算一條路徑。
- 情況二和情況三均需要進行旋轉處理,旋轉處理後無需繼續往上進行調整,是以說情況二一定是由情況一往上調整的過程中出現的。
出現叔叔存在且為黑時,單純使用變色已經無法處理了,這時我們需要進行旋轉處理。若祖孫三代的關系是直線(cur、parent、grandfather這三個結點為一條直線),則我們需要先進行單旋操作,再進行顔色調整,顔色調整後這棵被旋轉子樹的根結點是黑色的,是以無需繼續往上進行處理。
抽象圖表示如下:
說明一下: 當直線關系為,parent是grandfather的右孩子,cur是parent的右孩子時,就需要先進行左單旋操作,再進行顔色調整。
若祖孫三代的關系是折現(cur、parent、grandfather這三個結點為一條折現),則我們需要先進行雙旋操作,再進行顔色調整,顔色調整後這棵被旋轉子樹的根是黑色的,是以無需繼續往上進行處理。
抽象圖表示如下:
說明一下: 當折現關系為,parent是grandfather的右孩子,cur是parent的左孩子時,就需要先進行右左雙旋操作,再進行顔色調整。
情況三:插入結點的叔叔不存在。
在這種情況下的cur結點一定是新插入的結點,而不可能是由情況一變化而來的,因為叔叔不存在說明在parent的下面不可能再挂黑色結點了,如下圖:
如果插入前parent下面再挂黑色結點,就會導緻圖中兩條路徑黑色結點的數目不相同,而parent是紅色的,是以parent下面自然也不能挂紅色結點,是以說這種情況下的cur結點一定是新插入的結點。
和情況二一樣,若祖孫三代的關系是直線(cur、parent、grandfather這三個結點為一條直線),則我們需要先進行單旋操作,再進行顔色調整,顔色調整後這棵被旋轉子樹的根結點是黑色的,是以無需繼續往上進行處理。
抽象圖表示如下:
說明一下: 當直線關系為,parent是grandfather的右孩子,cur是parent的右孩子時,就需要先進行左單旋操作,再進行顔色調整。
若祖孫三代的關系是折現(cur、parent、grandfather這三個結點為一條折現),則我們需要先進行雙旋操作,再進行顔色調整,顔色調整後這棵被旋轉子樹的根是黑色的,是以無需繼續往上進行處理。
抽象圖表示如下:
說明一下: 當折現關系為,parent是grandfather的右孩子,cur是parent的左孩子時,就需要先進行右左雙旋操作,再進行顔色調整。
代碼如下:
//插入函數
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr) //若紅黑樹為空樹,則插入結點直接作為根結點
{
_root = new Node(kv);
_root->_col = BLACK; //根結點必須是黑色
return make_pair(_root, true); //插入成功
}
//1、按二叉搜尋樹的插入方法,找到待插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first < cur->_kv.first) //待插入結點的key值小于目前結點的key值
{
//往該結點的左子樹走
parent = cur;
cur = cur->_left;
}
else if (kv.first > cur->_kv.first) //待插入結點的key值大于目前結點的key值
{
//往該結點的右子樹走
parent = cur;
cur = cur->_right;
}
else //待插入結點的key值等于目前結點的key值
{
return make_pair(cur, false); //插入失敗
}
}
//2、将待插入結點插入到樹中
cur = new Node(kv); //根據所給值構造一個結點
Node* newnode = cur; //記錄新插入的結點(便于後序傳回)
if (kv.first < parent->_kv.first) //新結點的key值小于parent的key值
{
//插入到parent的左邊
parent->_left = cur;
cur->_parent = parent;
}
else //新結點的key值大于parent的key值
{
//插入到parent的右邊
parent->_right = cur;
cur->_parent = parent;
}
//3、若插入結點的父結點是紅色的,則需要對紅黑樹進行調整
while (parent&&parent->_col == RED)
{
Node* grandfather = parent->_parent; //parent是紅色,則其父結點一定存在
if (parent == grandfather->_left) //parent是grandfather的左孩子
{
Node* uncle = grandfather->_right; //uncle是grandfather的右孩子
if (uncle&&uncle->_col == RED) //情況1:uncle存在且為紅
{
//顔色調整
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//繼續往上處理
cur = grandfather;
parent = cur->_parent;
}
else //情況2+情況3:uncle不存在 + uncle存在且為黑
{
if (cur == parent->_left)
{
RotateR(grandfather); //右單旋
//顔色調整
grandfather->_col = RED;
parent->_col = BLACK;
}
else //cur == parent->_right
{
RotateLR(grandfather); //左右雙旋
//顔色調整
grandfather->_col = RED;
cur->_col = BLACK;
}
break; //子樹旋轉後,該子樹的根變成了黑色,無需繼續往上進行處理
}
}
else //parent是grandfather的右孩子
{
Node* uncle = grandfather->_left; //uncle是grandfather的左孩子
if (uncle&&uncle->_col == RED) //情況1:uncle存在且為紅
{
//顔色調整
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//繼續往上處理
cur = grandfather;
parent = cur->_parent;
}
else //情況2+情況3:uncle不存在 + uncle存在且為黑
{
if (cur == parent->_left)
{
RotateRL(grandfather); //右左雙旋
//顔色調整
cur->_col = BLACK;
grandfather->_col = RED;
}
else //cur == parent->_right
{
RotateL(grandfather); //左單旋
//顔色調整
grandfather->_col = RED;
parent->_col = BLACK;
}
break; //子樹旋轉後,該子樹的根變成了黑色,無需繼續往上進行處理
}
}
}
_root->_col = BLACK; //根結點的顔色為黑色(可能被情況一變成了紅色,需要變回黑色)
return make_pair(newnode, true); //插入成功
}
//左單旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentParent = parent->_parent;
//建立subRL與parent之間的聯系
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
//建立parent與subR之間的聯系
subR->_left = parent;
parent->_parent = subR;
//建立subR與parentParent之間的聯系
if (parentParent == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
//右單旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentParent = parent->_parent;
//建立subLR與parent之間的聯系
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
//建立parent與subL之間的聯系
subL->_right = parent;
parent->_parent = subL;
//建立subL與parentParent之間的聯系
if (parentParent == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
//左右雙旋
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
//右左雙旋
void RotateRL(Node* parent)
{
RotateR(parent->_right);
RotateL(parent);
} 注意: 在紅黑樹調整後,需要将根結點的顔色變為黑色,因為紅黑樹的根結點可能在情況一的調整過程中被變成了紅色。
紅黑樹的驗證
紅黑樹也是一種特殊的二叉搜尋樹,是以我們可以先擷取二叉樹的中序周遊序列,來判斷該二叉樹是否滿足二叉搜尋樹的性質。
代碼如下:
//中序周遊
void Inorder()
{
_Inorder(_root);
}
//中序周遊子函數
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_kv.first << " ";
_Inorder(root->_right);
} 但中序有序隻能證明是二叉搜尋樹,要證明二叉樹是紅黑樹還需驗證該二叉樹是否滿足紅黑樹的性質。
代碼如下:
//判斷是否為紅黑樹
bool ISRBTree()
{
if (_root == nullptr) //空樹是紅黑樹
{
return true;
}
if (_root->_col == RED)
{
cout << "error:根結點為紅色" << endl;
return false;
}
//找最左路徑作為黑色結點數目的參考值
Node* cur = _root;
int BlackCount = 0;
while (cur)
{
if (cur->_col == BLACK)
BlackCount++;
cur = cur->_left;
}
int count = 0;
return _ISRBTree(_root, count, BlackCount);
}
//判斷是否為紅黑樹的子函數
bool _ISRBTree(Node* root, int count, int BlackCount)
{
if (root == nullptr) //該路徑已經走完了
{
if (count != BlackCount)
{
cout << "error:黑色結點的數目不相等" << endl;
return false;
}
return true;
}
if (root->_col == RED&&root->_parent->_col == RED)
{
cout << "error:存在連續的紅色結點" << endl;
return false;
}
if (root->_col == BLACK)
{
count++;
}
return _ISRBTree(root->_left, count, BlackCount) && _ISRBTree(root->_right, count, BlackCount);
} 紅黑樹的查找
紅黑樹的查找函數與二叉搜尋樹的查找方式一模一樣,邏輯如下:
- 若樹為空樹,則查找失敗,傳回nullptr。
- 若key值小于目前結點的值,則應該在該結點的左子樹當中進行查找。
- 若key值大于目前結點的值,則應該在該結點的右子樹當中進行查找。
- 若key值等于目前結點的值,則查找成功,傳回對應結點。
代碼如下:
//查找函數
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key < cur->_kv.first) //key值小于該結點的值
{
cur = cur->_left; //在該結點的左子樹當中查找
}
else if (key > cur->_kv.first) //key值大于該結點的值
{
cur = cur->_right; //在該結點的右子樹當中查找
}
else //找到了目标結點
{
return cur; //傳回該結點
}
}
return nullptr; //查找失敗
} 紅黑樹的删除
紅黑樹的删除要比插入更加難以了解,但是隻要仔細一點也還行。
第一步:找到實際待删除的結點
找結點的過程與二叉搜尋樹尋找待删除結點的方法一樣,若找到的待删除結點的左右子樹均不為空,則需要使用替換法進行删除。是以我們最終需要删除的都是左右子樹至少有一個為空的結點。
找到實際待删除結點後,先不删除該結點,否則調整紅黑樹時不容易控制,找到實際待删除結點後立即進行紅黑樹的調整。
第二步:調整紅黑樹
調整紅黑樹之前,我們先判斷一下本次結點的删除是否會破壞了紅黑樹的性質,若破壞了我們才需要對紅黑樹進行調整。
若實際删除的結點是紅色結點,那麼本次删除操作不會破壞紅黑樹的性質,是以我們不需要對紅黑樹進行調整。反之,若删除的結點是黑色結點,我們就需要對紅黑樹進行調整,因為黑色結點的删除将會使得一些路徑中黑色結點的數目減少,此時便破壞了紅黑樹的性質四。
我們先來說最簡單的一種情況,即待删除結點隻有一個孩子為空的情況。
在這種情況下,待删除結點要麼是隻有左孩子,要麼是有隻右孩子,但不管是左孩子還是右孩子,這個孩子一定是紅色的,因為若這個孩子是黑色的,那麼此時圖示長藍色路徑的黑色結點數目比短藍色路徑的黑色結點數目多,不符合紅黑樹的性質。
又因為紅黑樹當中不允許出現連續的紅色結點,是以在這種情況下實際上就隻有圖示兩種實際情況,這時我們直接将待删除結點的那個紅孩子變成黑色就行了,因為在後面實際删除結點時會将這個孩子連接配接到删除結點的父結點下面,連接配接後相當于我們删除的是一個紅色結點,紅黑樹調整完成。
下面再來說比較複雜的情況,即待删除結點的左右孩子均為空。
我們以待删除結點是其父結點的左孩子為例,分為以下四種情況:
圖示說明:
- 若parent結點為白色,表明parent結點可能是紅色結點也可能是黑色結點。
- 若bL或bR結點為白色,表明其可能是紅色結點或黑色結點甚至該結點不存在。
- bL和bR結點為黑色時,表明他們可能是黑色結點或該結點不存在。
情況一:brother為紅色。
當待删除結點的brother為紅色時,我們先以parent為旋轉點進行一次左單旋,再将brother的顔色變為黑色,将parent的顔色變為紅色,此時我們再對待删除結點cur進行情況分析,情況一就轉換成了情況二、三或四。情況二:brother為黑色,且其左右孩子都是黑色結點或為空。
在該情況下,我們直接将brother的顔色變成紅色,此時根據parent的顔色決定紅黑樹的調整是否結束,若parent的顔色是紅色,則我們将parent變為黑色後即可結束紅黑樹的調整;若parent的顔色原本就是黑色,則我們需要将parent結點當作下一次調整時的cur結點進行情況分析,并且情況二在下一次調整時可能會是情況一、二、三、四當中的任何一種。情況三:brother為黑色,且其左孩子是紅色結點,右孩子是黑色結點或為空。
出現該情況時,我們先以brother為旋轉點進行一次右單旋,再将brother結點變為紅色,将brotherLeft變為黑色,此時我們再對待删除結點cur進行情況分析,情況三就轉換成了情況四。情況四:brother為黑色,且其右孩子是紅色結點。
經過情況四的處理後,紅黑樹就一定調整結束了。在情況四當中,我們先以parent為旋轉點進行一次左單旋,然後将parent的顔色指派給brother,再将parent的顔色變為黑色,最後将brotherRight變為黑色,此時紅黑樹的調整便結束了。
說明一下:
- 待删除結點是其父結點的右孩子時的四種情況與上面四種情況類似,這裡就不列舉出來了。
- 若待删除結點沒有父結點,即待删除結點是根結點時,在找到該結點時就進行了删除,這裡不用考慮,具體看代碼。
這裡有必要對各種情況的切換進行說明,你可能會擔心調整紅黑樹時在這四種情況當中一直來回切換而不能跳出,下面我們來對此進行分析:
首先,進入情況四後紅黑樹就一定調整結束了。其次,進入情況三後,下次也一定會進入情況四,紅黑樹的調整也會結束。是以情況三和情況四是沒有問題的,你們最糾結的隻能是情況一和情況二了。
情況一又會切換為情況二、三、四,是以隻要情況二能夠有辦法退出,那麼所有情況就都能退出了。
在情況二當中我們說,如果parent的顔色是紅色,那麼我們将parent變為黑色後就可以結束紅黑樹的調整,那會不會每次進入情況二時parent的顔色都不是紅色,而一直是黑色的呢?
當然有可能,但是我們若一直往上進行調整時,那麼總會調整到紅黑樹的根結點,當調整到根結點後我們便不用進行調整了,此時根結點雖然是黑色的,但是不影響,這僅僅意味着每條從根到葉子的路徑上包含的黑色結點的個數都增加了一個,此時也沒有破壞紅黑樹的性質,也就完成了紅黑樹的調整,是以在調整過程中不會出現一直在這四種情況來回切換而不能跳出的問題。
第三步:進行結點的實際删除
在紅黑樹調整完畢後,我們就可以進行結點的删除了,删除結點的方式很簡單,若待删除結點有左孩子或右孩子,我們将其左孩子或右孩子連接配接到待删除結點父結點的下面即可,之後便可以将待删除結點删除了。
代碼如下:
//删除函數
bool Erase(const K& key)
{
//用于周遊二叉樹
Node* parent = nullptr;
Node* cur = _root;
//用于标記實際的待删除結點及其父結點
Node* delParentPos = nullptr;
Node* delPos = nullptr;
while (cur)
{
if (key < cur->_kv.first) //所給key值小于目前結點的key值
{
//往該結點的左子樹走
parent = cur;
cur = cur->_left;
}
else if (key > cur->_kv.first) //所給key值大于目前結點的key值
{
//往該結點的右子樹走
parent = cur;
cur = cur->_right;
}
else //找到了待删除結點
{
if (cur->_left == nullptr) //待删除結點的左子樹為空
{
if (cur == _root) //待删除結點是根結點
{
_root = _root->_right; //讓根結點的右子樹作為新的根結點
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //根結點為黑色
}
delete cur; //删除原根結點
return true;
}
else
{
delParentPos = parent; //标記實際删除結點的父結點
delPos = cur; //标記實際删除的結點
}
break; //進行紅黑樹的調整以及結點的實際删除
}
else if (cur->_right == nullptr) //待删除結點的右子樹為空
{
if (cur == _root) //待删除結點是根結點
{
_root = _root->_left; //讓根結點的左子樹作為新的根結點
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //根結點為黑色
}
delete cur; //删除原根結點
return true;
}
else
{
delParentPos = parent; //标記實際删除結點的父結點
delPos = cur; //标記實際删除的結點
}
break; //進行紅黑樹的調整以及結點的實際删除
}
else //待删除結點的左右子樹均不為空
{
//替換法删除
//尋找待删除結點右子樹當中key值最小的結點作為實際删除結點
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
cur->_kv.first = minRight->_kv.first; //将待删除結點的key改為minRight的key
cur->_kv.second = minRight->_kv.second; //将待删除結點的value改為minRight的value
delParentPos = minParent; //标記實際删除結點的父結點
delPos = minRight; //标記實際删除的結點
break; //進行紅黑樹的調整以及結點的實際删除
}
}
}
if (delPos == nullptr) //delPos沒有被修改過,說明沒有找到待删除結點
{
return false;
}
//記錄待删除結點及其父結點(用于後續實際删除)
Node* del = delPos;
Node* delP = delParentPos;
//調整紅黑樹
if (delPos->_col == BLACK) //删除的是黑色結點
{
if (delPos->_left) //待删除結點有一個紅色的左孩子(不可能是黑色)
{
delPos->_left->_col = BLACK; //将這個紅色的左孩子變黑即可
}
else if (delPos->_right) //待删除結點有一個紅色的右孩子(不可能是黑色)
{
delPos->_right->_col = BLACK; //将這個紅色的右孩子變黑即可
}
else //待删除結點的左右均為空
{
while (delPos != _root) //可能一直調整到根結點
{
if (delPos == delParentPos->_left) //待删除結點是其父結點的左孩子
{
Node* brother = delParentPos->_right; //兄弟結點是其父結點的右孩子
//情況一:brother為紅色
if (brother->_col == RED)
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateL(delParentPos);
//需要繼續處理
brother = delParentPos->_right; //更新brother(否則在本循環中執行其他情況的代碼會出錯)
}
//情況二:brother為黑色,且其左右孩子都是黑色結點或為空
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//需要繼續處理
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//情況三:brother為黑色,且其左孩子是紅色結點,右孩子是黑色結點或為空
if ((brother->_right == nullptr) || (brother->_right->_col == BLACK))
{
brother->_left->_col = BLACK;
brother->_col = RED;
RotateR(brother);
//需要繼續處理
brother = delParentPos->_right; //更新brother(否則執行下面情況四的代碼會出錯)
}
//情況四:brother為黑色,且其右孩子是紅色結點
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_right->_col = BLACK;
RotateL(delParentPos);
break; //情況四執行完畢後調整一定結束
}
}
else //delPos == delParentPos->_right //待删除結點是其父結點的左孩子
{
Node* brother = delParentPos->_left; //兄弟結點是其父結點的左孩子
//情況一:brother為紅色
if (brother->_col == RED) //brother為紅色
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateR(delParentPos);
//需要繼續處理
brother = delParentPos->_left; //更新brother(否則在本循環中執行其他情況的代碼會出錯)
}
//情況二:brother為黑色,且其左右孩子都是黑色結點或為空
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//需要繼續處理
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//情況三:brother為黑色,且其右孩子是紅色結點,左孩子是黑色結點或為空
if ((brother->_left == nullptr) || (brother->_left->_col == BLACK))
{
brother->_right->_col = BLACK;
brother->_col = RED;
RotateL(brother);
//需要繼續處理
brother = delParentPos->_left; //更新brother(否則執行下面情況四的代碼會出錯)
}
//情況四:brother為黑色,且其左孩子是紅色結點
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_left->_col = BLACK;
RotateR(delParentPos);
break; //情況四執行完畢後調整一定結束
}
}
}
}
}
//進行實際删除
if (del->_left == nullptr) //實際删除結點的左子樹為空
{
if (del == delP->_left) //實際删除結點是其父結點的左孩子
{
delP->_left = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
else //實際删除結點是其父結點的右孩子
{
delP->_right = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
}
else //實際删除結點的右子樹為空
{
if (del == delP->_left) //實際删除結點是其父結點的左孩子
{
delP->_left = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
else //實際删除結點是其父結點的右孩子
{
delP->_right = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
}
delete del; //實際删除結點
return true;
} 紅黑樹與AVL樹的比較
- AVL樹是通過控制左右高度差不超過1來實作二叉樹平衡的,實作的是二叉樹的嚴格平衡。
- 紅黑樹是通過控制結點的顔色,進而使得紅黑樹當中最長可能路徑不超過最短可能路徑的2倍,實作的是近似平衡。