2010年計算機聯考真題——一維數組循環左移

前記

從七月份決定開始考研，中間由于聽報告，回家複習數學和政治而耽誤了一些時間。自己準備報考山東大學計算機技術的專碩，幸好是數學是考數學二，專業課也隻有一門資料結構，這位我的複習節省了很多時間，不想數學一和統考的計算機基礎綜合的專業複習那麼費勁。現在資料結構的複習完全是參照《王道考研系列——2018年資料結構考研複習指導》在複習。對于資料結構雖然到時候是手寫算法，但是畢竟這是程式設計，對于算法能否正确實作并符合題目要求，隻有跑程式才能看見。是以複習的同時，有也想利用好csdn部落格來記錄自己複習過程，故現在開始把指導書上的所有題與基礎算法和資料結構利用部落格來記錄一下。

題目

設将n(n,1)個整數存放到一維數組R中，試設計一個在時間和空間兩方面盡可能有效的算法，将R中保有的序列循環左移P（0﹤P﹤n）個位置，即将R中的資料由（X0 X1 ……Xn-1）變換為（Xp Xp+1 ……Xn-1 X0 X1 ……Xp-1）要求：

　　（1）給出算法的基本設計思想。

　　（2）根據設計思想，采用C或C++或JAVA語言表述算法，關鍵之處給出注釋。

　　（3）說明你所設計算法的時間複雜度和空間複雜度

思路

對于這個問題：可以把問題轉化為把數組的前p個數與後n-p個數進行位置互換。即把後n-p個數整體放到前p個數的前面即可。

代碼

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std;

//把下标在[left,right]的數進行逆置 
bool Reverse(int* A ,int left , int right , int size)
{
    if(left >= right || right >= size)
        return false;
    int mid = (left+right)/2;
    for(int i = 0 ; i < mid - left ; i++){
        A[i+left] += A[right-i];
        A[right-i] = A[i+left] - A[right-i];
        A[i+left] -= A[right-i];
    }
    return true;
}

//把前ｍ個數與後ｎ個數互換位置 
void Exchange(int* A ,int m, int n ,int size) 
{
    Reverse(A,0,m+n-1,size);        //下标０～ｍ+n-1的數逆置
    Reverse(A,0,n-1,size);          //下标０～n-1的數逆置
    Reverse(A,n,m+n-1,size);        //下标n～ｍ+n-1的數逆置 
}

int main()
{
    int a[7];
    for(int i = 0 ; i < 7 ; i++){
        a[i] = i+1;
    } 

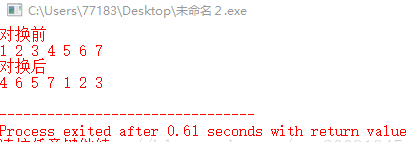
    cout<<"對換前"<<endl;
    for(int i = 0 ; i< 7 ; i++){
        cout<<a[i]<<" ";
    }
    cout<<endl;

    Exchange(a ,3,4,7);
    cout<<"對換後"<<endl;
    for(int i = 0 ; i< 7 ; i++){
        cout<<a[i]<<" ";
    }
    cout<<endl;

    return 0;
}           

複制