概述
這是自己這學期算法課的實驗作業。下面給出漢密爾頓圖的定義。定義如下:對于連通圖G=(V,E),V1,V2,…,Vn是G 的一條通路,且圖中任意兩個頂點都可達,若 中每個頂點在該通路中出現且僅出現一次,則稱該通路為漢密爾頓通路。若 V1=Vn,則稱該通路為漢密爾頓回路。
算法描述
1)初始化最佳路徑數組best_path,同時初始化臨時路徑數組path與通路數組isvisited,設定最小長度min,設定長度變量length = 0
2)開始對每個頂點進行周遊尋找最佳路徑,首先堆通路數組中對應頂點進行置1,并把目前頂點追加到path,同時利用cur_vertex這個臨時變量儲存目前結點,并開始進行循環。
3)找到出cur_vertex之外與之相鄰且并未通路的一個頂點k,利用tmp儲存這兩點之間的權重,之後檢查是否存在比tmp更小且與cur_vertex相鄰的頂點,如有則更新tmp與通路的頂點k,之後更新length += tmp,以及更新cur_vertex = k,如果length大于min,則說明改路徑無效,跳出循環。
4)重複步驟3周遊每一個結點。循環結束後,對length更新,加上最後一個結點到cur_vertex結點的距離。這是如果min大于legnth,則對min更新,并把path數組複制到best_path中去。
5)重複步驟2)直至周遊完每個結點。傳回最小長度。
//求漢密爾頓回路函數
int Hanmilton(){
int path[1000] = {0};
int cur_vertex = 0; //作為儲存目前結點
int length = 0; //漢密爾頓回路長度
int min = 10000; //最小長度
for(int i = 1 ; i < this->Nv+1 ; i++){//對每個頂點為初始點進行比周遊尋找漢密爾頓回路
length = 0; //重新設定最端長度為0
memset(this->isvisited,0,sizeof(this->isvisited[0])*(this->Nv+1)); //重新初始化通路數組為0
this->isvisited[i] = 1; //标記目前結點為已通路
path[1] = i; //儲存到臨時路徑數組的第一個
cur_vertex = i; //儲存目前頂點
for(int j = 2 ; j < this->Nv+1 ; j++){//通路剩餘的結點
int k = 0;
//尋找到第一個未通路的結點
for(k = 2 ; k < this->Nv+1 ; k++){
if(this->isvisited[k] == 0){
break;
}
}
int tmp = this->data[cur_vertex][k]; //儲存目前頂點到該結點的路徑長度
for(int m = k+1 ; m < this->Nv+1 ; m++){//向後尋找有沒有路徑更短的節點
if((!this->isvisited[m]) && (tmp > this->data[cur_vertex][m])){
tmp = this->data[cur_vertex][m];//更新目前最短路徑
k = m;//更新第一個未被通路的結點
}
}
path[j] = k; //儲存路徑上的結點
this->isvisited[k] = 1; //标記為已通路
cur_vertex = k; //跟新目前結點
length += tmp; //跟新長度
if(length > min){ //目前長度大于最小長度,則改路徑無效,跳出循環
break;
}
}
length += this->data[cur_vertex][i];
if(min > length){ //更新最小長度并儲存最佳路徑
min = length;
for(int m = 0 ; m < this->Nv+1 ; m++){
this->best_path[m] = path[m];
}
}
}
//傳回最小長度
return min;
} 複制
例子
下面的例子是基于如下圖結構:
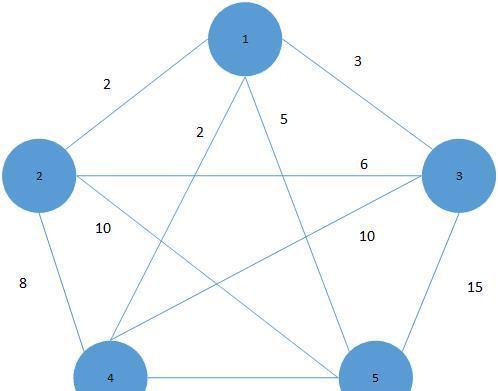
全部代碼如下:
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>
using namespace std;
/*
邊與邊長:(起點,終點,長度)
1 2 2
1 3 3
1 4 2
1 5 5
2 3 6
2 4 8
2 5 10
3 4 10
3 5 15
4 5 12
*/
class Graph{
private:
int** data; //鄰接矩陣 到sa 拉黑聖誕節,
int* isvisited; //通路數組
int Nv; //頂點數
int Ne; //邊數
vector<int> best_path; //漢密爾頓最佳路徑
public:
//構造函數
Graph(int nv,int ne){
this->Nv = nv;
this->Ne = ne;
this->data = new int*[nv+1];
best_path.reserve(nv+1);
for(int i = 0 ; i < nv+1 ; i++){
best_path[i] = 0;
}
//初始化通路數組
this->isvisited = new int[nv+1];
memset(this->isvisited,0,sizeof(this->isvisited[0])*(nv+1));
//對鄰接矩陣進行初始化
for(int i = 0 ; i < nv+1 ; i++){
data[i] = new int[nv+1];
memset(data[i],0,sizeof(data[i][0])*(nv+1));
}
cout<<"請輸入邊與邊長:"<<endl;
//對邊進行初始化
for(int i = 0 ; i < ne ; i++){
int v1,v2,weight;
cin>>v1>>v2>>weight;
this->data[v1][v2] = this->data[v2][v1] = weight;
}
}
//求漢密爾頓回路函數
int Hanmilton(){
int path[1000] = {0};
int cur_vertex = 0; //作為儲存目前結點
int length = 0; //漢密爾頓回路長度
int min = 10000; //最小長度
for(int i = 1 ; i < this->Nv+1 ; i++){//對每個頂點為初始點進行比周遊尋找漢密爾頓回路
length = 0; //重新設定最端長度為0
memset(this->isvisited,0,sizeof(this->isvisited[0])*(this->Nv+1)); //重新初始化通路數組為0
this->isvisited[i] = 1; //标記目前結點為已通路
path[1] = i; //儲存到臨時路徑數組的第一個
cur_vertex = i; //儲存目前頂點
for(int j = 2 ; j < this->Nv+1 ; j++){//通路剩餘的結點
int k = 0;
//尋找到第一個未通路的結點
for(k = 2 ; k < this->Nv+1 ; k++){
if(this->isvisited[k] == 0){
break;
}
}
int tmp = this->data[cur_vertex][k]; //儲存目前頂點到該結點的路徑長度
for(int m = k+1 ; m < this->Nv+1 ; m++){//向後尋找有沒有路徑更短的節點
if((!this->isvisited[m]) && (tmp > this->data[cur_vertex][m])){
tmp = this->data[cur_vertex][m];//更新目前最短路徑
k = m;//更新第一個未被通路的結點
}
}
path[j] = k; //儲存路徑上的結點
this->isvisited[k] = 1; //标記為已通路
cur_vertex = k; //跟新目前結點
length += tmp; //跟新長度
if(length > min){ //目前長度大于最小長度,則改路徑無效,跳出循環
break;
}
}
length += this->data[cur_vertex][i];
if(min > length){ //更新最小長度并儲存最佳路徑
min = length;
for(int m = 0 ; m < this->Nv+1 ; m++){
this->best_path[m] = path[m];
}
}
}
//傳回最小長度
return min;
}
//列印最佳漢密爾頓回路
void Print_Best_Path(){
cout<<this->best_path[1];
for(int i = 2 ; i < this->Nv+1 ; i++){
cout<<" -> "<<this->best_path[i];
}
cout<<" -> "<<this->best_path[1];
}
//列印鄰接矩陣
void Print(){
for(int i = 1 ; i < this->Nv+1 ; i++){
for(int j = 1 ; j < this->Nv+1 ; j++){
printf("%3d",this->data[i][j]);
}
cout<<endl;
}
}
};
int main()
{
cout<<"請輸入頂點數與邊數:"<<endl;
int nv,ne;
cin>>nv>>ne;
Graph graph(nv,ne);
cout<<"鄰接矩陣為:"<<endl;
graph.Print();
cout<<"該圖的漢密爾頓回路長度為:"<<endl;
int length = 0;
length = graph.Hanmilton();
cout<<length<<endl;
cout<<"漢密爾頓回路路徑為:"<<endl;
graph.Print_Best_Path();
return 0;
} 複制
運作結果如下: