與簡單的加法運算相比,乘法運算具有更高的計算複雜度。深度神經網絡中廣泛使用的卷積正好是來度量輸入特征和卷積濾波器之間的相似性,這涉及浮點值之間的大量乘法。現在作者提出了加法網絡(AdderNets)來交換深度神經網絡中的這些大規模乘法,特别是卷積神經網絡(CNNs),以獲得更簡易的加法以降低計算成本。
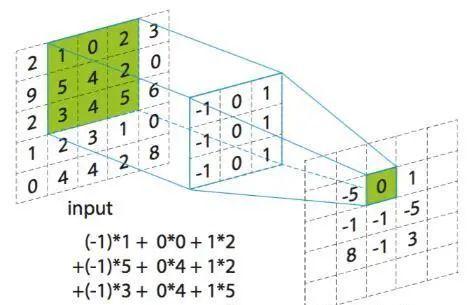
在加法器網中,作者以濾波器與輸入特征之間的L1範數距離作為輸出響應。分析了這種新的相似性度量對神經網絡優化的影響。為了獲得更好的性能,通過研究全精度梯度開發了一種特殊的反向傳播方法。然後,作者還提出了一種自适應學習率政策,根據每個神經元梯度的大小來增強加法網絡的訓練過程。
上圖就是加法網絡的特征可視化結果。
研究背景
雖然深度神經網絡的二值化濾波器大大降低了計算成本,但原始識别精度往往無法保持。此外,二進制網絡的訓練過程不穩定,通常要求較慢的收斂速度和較小的學習速率。經典CNN中的卷積實際上是測量兩個輸入的相似性。研究人員和開發人員習慣于将卷積作為預設操作,從視覺資料中提取特征,并引入各種方法來加速卷積,即使存在犧牲網絡能力的風險。但幾乎沒有人試圖用另一種更有效的相似性度量來取代卷積。事實上,加法的計算複雜度要比乘法低得多。是以,作者有動機研究用卷積神經網絡中的加法代替乘法的可行性。
相關工作
Network Pruning
網絡剪枝主要通過移除備援的權重來實作網絡的壓縮和加速。比如用奇異值分解(SVD)全連接配接層的權重矩陣、去除預訓練中的部分權重、将filter變換到頻域避免浮點計算。還有的通過去除備援的filter、或者對channel進行選擇這樣備援filter/channel後續的計算就無需考慮了。
Efficient Blocks Design
許多工作不是直接降低預先訓練的神經網絡的計算複雜度,而是集中在設計新的子產品或操作來取代傳統的卷積濾波器。Landola等人(Forrest N Iandola, Song Han, Matthew W Moskewicz,Khalid Ashraf, William J Dally, and Kurt Keutzer.Squeezenet: Alexnet-level accuracy with 50x fewer parameters and¡ 0.5 mb model size. 2017)引入了瓶頸結構,大大降低了CNN的計算成本。Howard等人(Andrew G Howard, Menglong Zhu, Bo Chen, DmitryKalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, and Hartwig Adam. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXivpreprint arXiv:1704.04861, 2017)設計了移動網絡,它将傳統的卷積濾波器分解為點和深度卷積濾波器,FLOPs要少得多。張等人(Xiangyu Zhang, Xinyu Zhou, Mengxiao Lin, and Jian Sun.Shufflenet: An extremely efficient convolutional neural network for mobile devices. In CVPR, pages 6848–6856, 2018)組合群卷積和信道洗牌操作,以建立有效的神經網絡與較少的計算。胡等人(Jie Hu, Li Shen, and Gang Sun. Squeeze-and-excitation networks. In CVPR, pages 7132–7141, 2018)提出了擠壓和激勵塊,該子產品通過模組化信道之間的互相依賴關系來關注信道的關系,以稍微增加的計算成本來提高性能。吳等人(Bichen Wu, Alvin Wan, Xiangyu Yue, Peter Jin, SichengZhao, Noah Golmant, Amir Gholaminejad, Joseph Gonzalez, and Kurt Keutzer. Shift: A zero flop, zero parameteralternative to spatial convolutions. In CVPR, pages 9127–9135, 2018)提出了一種無參數的“移位”操作,該操作具有零失敗和零參數,以取代傳統濾波器,大大降低了CNN的計算和存儲成本。鐘等人 (Huasong Zhong, Xianggen Liu, Yihui He, Yuchun Ma, andKris Kitani. Shift-based primitives for efficient convolutionalneural networks. arXiv preprint arXiv:1809.08458, 2018)進一步将基于移位的原理推入信道移位、位址移位和快捷移位,以減少GPU上的推理時間,同時保持性能。Wang等人(Yunhe Wang, Chang Xu, Chunjing Xu, Chao Xu, andDacheng Tao. Learning versatile filters for efficient convolutional neural networks. In NeuriPS, pages 1608–1618, 2018)開發了多功能卷積濾波器,利用較少的計算和參數生成更有用的特征。
Knowledge Distillation
除了去除網絡中的備援連接配接,Hinton還提出了knowledge distillation的概念,借助teacher網絡的學習能力來指導student網絡完成複雜任務的學習,變種有多個teacher網絡、對中間隐層的學習以及對不同teacher網絡學到的特征整合成新的知識來幫助student網絡的訓練。
Adder Network
不同類别的CNN特征按其角度來劃分。由于AdderNet使用L1範數來區分不同的類,是以AdderNet的特征傾向于聚集到不同的類中心。
對于CNN中的卷積運算,假定輸入X,filter表示為F,卷積後輸出的是二者的相似性度量,表述如下面公式:
實際上二者的相似性度量可以有多種途徑,但都涉及到大量的乘法運算,這就增加了計算開銷。是以作者通過計算L1距離完成輸入和filter之間的相似性度量。而L1距離僅涉及到兩個向量差的絕對值,這樣輸出就變成了如下:
我們注意到使用互相關運算還是L1距離都可以完成相似性度量,但二者的輸出結果還是有一些差别的。通過卷積核完成輸入特征圖譜的權重和計算,結果可正可負;但adder filter輸出的結果恒為負,為此作者引入了batch normalization将結果歸一化到一定範圍區間内進而保證傳統CNN使用的激活函數在此依舊可以正常使用。雖然BN的引入也有乘法操作但計算複雜度已遠低于正常卷積層。conv和BN的計算複雜度分别如下:
Optimization
神經網絡利用反向傳播來計算濾波器的梯度和随機梯度下降來更新參數。在CNN中,輸出特征Y相對于濾波器F的偏導數被計算為:
但是在AdderNets中,Y相對于濾波器F的偏導數是:
但signSGD優化方法幾乎不會選擇到最陡的方向,而且随着次元增加效果會更差,是以本文使用如下公式進行梯度更新:
此外,如果使用full-precision gradient的更新方法,由于涉及到前層的梯度值很容易導緻梯度爆炸,是以本文還通過使用HardTanh将輸出限定在[-1,1]範圍内。
輸出特征Y相對于輸入特征X的偏導數計算為:
Adaptive Learning Rate Scaling
在傳統的CNN中,假設權值和輸入特征是獨立的,服從正态分布,輸出的方差大緻可以估計為:
相反,對于AdderNets,輸出的方差可以近似為:
AdderNets的輸出具有較大方差,在更新時根據正常的鍊式法則會導緻梯度比正常CNN更小,進而導緻參數更新過慢。是以自然而然想到通過引入自适應學習率調整參數的更新learningrate組成:
包括神經網絡的全局學習率和本地學習率,其中本地學習率表示為:
這樣可以保證每層更新的幅度一緻,最終AdderNet的訓練過程表述為:
實驗
在MNIST、CIFAR及ImageNet資料集山驗證了AdderNet的有效性,随後進行了消融實驗以及對提取的特征進行可視化。實驗平台和架構:V100 Pytorch。
CIFAR-10和CIFAR-100 datasets分類結果
ImageNet datasets分類結果
AdderNet使用L1距離來度量輸入與filter之間的關系,而不是使用卷積的互相關。是以需要探究一些AdderNet與CNN特征空間上的差異。是以就在MNIST資料集上搭建了LeNet++:6conv+1fc,每層神經元數目依次為:32,32,64,64,128,128,2。同樣其中的conv層用add filter替換可視化結果如圖1所示,CNN的可視化結果為右側,相似度通過cosin計算得到的,是以分類通過角度進行的分類。左側是AdderNet的可視化結果,可以看到不同種類的聚類中心不同,這也驗證了AdderNet具有同CNN相似的辨識能力。
對filter的可視化結果如上圖所示,雖然AdderNet和CNN用的度量矩陣不同,但都具有特征提取的能力。
Learning curve of AdderNets using different optimization schemes
權重分布的可視化
對LeNet-5-BN的第三層進行可視化,AdderNet權重更接近Laplace分布,CNN的權重近似高斯分布,分别對應L1-norm和L2-norm。
注:左邊是AdderNet,右邊是CNNs