1)畫圖及文字解釋p74頁下半頁關于LAR算法所定義的一系列向量的幾何意義,及整個算法的幾何意義
回歸模型:
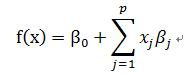
(共有p個變量)
給出具有n個樣本的樣本矩陣:
(j=1,...,p)
LAR算法:
1.标準化、中心化資料(使各向量為機關向量,且
)
殘差:
初始系數:
2.(1)目前殘差
找出Xj,使得
,Xj對應系數
(2)将從0到
增大,直到出現Xk,使得
,其中
為目前殘差
(3)改變Xj,Xk的系數,使向量
沿着Xj,Xk的角平分線移動,直到出現Xl,使得
為目前殘差(圖中平移向量使得Xj,Xk,r2在同一起始點,Xj的系數從第一步賦予的值開始增大)
2.重複以上步驟,每一次改變系數使得向量在所有已選擇向量的角平分線上移動,得到新的向量,新的向量與目前殘差的相關系數與已選擇向量和目前殘差的相關系數相等,直到所有向量都被選中,所得到的系數即可确定回歸方程。
2)畫圖及文字解釋p76頁關于了解LAR和Lasso的軌迹圖為何如此相像
QQ圖檔20160323195642.jpg (375.77 KB)
下載下傳附件 儲存到相冊
2016-3-23 19:58 上傳
Lasso搜尋路徑受條件影響,L.Arc Length從0增長時,正方形不斷變大,但在一定範圍内,
始終為0,
不斷增大,直到加入。而LAR算法在執行第二步算法時,增大,
始終為0,直到找到Xk,加入後才有變化,是以兩者軌迹相似。
3)解釋增強LAR算法為什麼可以進行變量淘汰
第三題不太懂。不知道是不是因為變量間存在多重共線性,選擇其中一個即可。共線的向量隻選擇一個。
參考資料:
煉數成金 畫圖解釋p74頁關于LAR算法所定義的一系列向量的幾何意義 ,了解LAR和Lasso的軌迹
http://f.dataguru.cn/forum.php?m ... 1&highlight=LAR