K-means算法詳解及實作

文章目錄

- 一、原理和流程
- - 1、原理
  - 2、流程
- 二、K-means中常用的到中心距離的度量有哪些
- 三、K-means中的k值如何選取
- - 1、手肘法
  - 2、輪廓系數法
  - 3、總結
- 四、代碼實作
- 五、其他問題的解答
- References

主要的KMeans算法的原理和應用，在學習典過程中，我們要帶着以下幾個問題去學習

以下問題摘自于https://blog.csdn.net/qq_33011855/article/details/81482511

1、簡述一下K-means算法的原理和工作流程

2、K-means中常用的到中心距離的度量有哪些？

3、K-means中的k值如何選取?

4、K-means算法中初始點的選擇對最終結果有影響嗎？

5、K-means聚類中每個類别中心的初始點如何選擇？

6、K-means中空聚類的處理

7、K-means是否會一直陷入選擇質心的循環停不下來？

8、如何快速收斂資料量超大的K-means？

9、K-means算法的優點和缺點是什麼？

一、原理和流程

1、原理

對給定的無标記的樣本資料集，事先确定聚類簇數K，讓簇内的樣本盡可能緊密分布在一起，使簇間的距離盡可能大。K-Means作為無監督的聚類算法，其類似于全自動分類，簇内越相似，聚類效果越好，實作較簡單，聚類效果好，是以被廣泛使用。用以下的效果圖更能直覺地看出其過程：

K-means算法詳解及實作

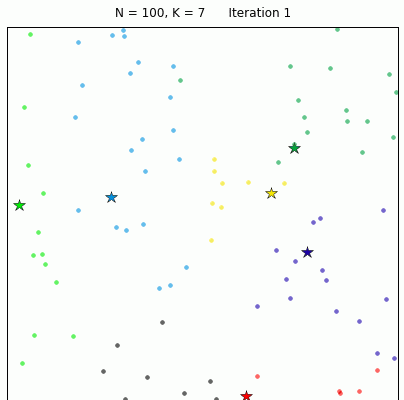
2、流程

（1）随即确定K個初始點作為質心（這裡如何确定k将在下面給出解釋）

（2）将資料集中的每個點配置設定到一個簇中，即為每個點找距離其最近的質心，并将其配置設定給質心所對應的簇

（3）簇分好後，計算每個簇所有點的平均值，将平均值作為對應簇新的質心

（4）循環2、3步驟，直到質心不變

Step1：從資料集D中随機選擇k個樣本作為初始的k個質心向量
Step2：計算資料集中樣本Xi分别到k個質心的歐幾裡得距離d1, d2……dk. 于是我們得到與Xi距離最小的質心并且把Xi劃分到和這個質心同一cluster中。
Step3：對資料集中所有樣本進行Step2操作
Step4：重新計算k個簇裡面的向量均值（就是把k個質心在新的簇下重新整理一遍），然後重複Step2- Step4。直到所有的k個質心向量都沒有發生變化。

僞代碼是：（要會寫）

建立k個點作為起始質心（經常是随機選擇）
當任意一個點的簇配置設定結果發生改變時
	對資料集中的每個資料點
		對每個質心
			計算質心和資料點之間的距離
		将資料點配置設定到距離其最近的簇
	對每一個簇，計算簇中所有點的均值并将均值作為新的質心

上面“最近”質心，意味着需要進行某種距離的計算，即下文要介紹的K-means中常用的到中心距離的度量有哪些？

二、K-means中常用的到中心距離的度量有哪些

這裡最常用的有以下兩種（我們這裡隻簡單介紹下二維的）

曼哈頓距離

d 12 = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d _ { 12 } = \left| x _ { 1 } - x _ { 2 } \right| + \left| y _ { 1 } - y _ { 2 } \right| d12=∣x1−x2∣+∣y1−y2∣
歐幾裡得距離（别稱“歐式距離”）

d 12 = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d _ { 12 } = \sqrt { \left( x _ { 1 } - x _ { 2 } \right) ^ { 2 } + \left( y _ { 1 } - y _ { 2 } \right) ^ { 2 } } d12=(x1−x2)2+(y1−y2)2

假設兩個點坐标是（1，1），（4，5）
則曼哈頓距離是7，歐式距離是5

K-means算法詳解及實作

補充：（圖檔來源）

K-means算法詳解及實作

聚類分析的類間距離度量方法

三、K-means中的k值如何選取

以下博文轉自：https://blog.csdn.net/qq_15738501/article/details/79036255

通常我們會采用手肘法來确定k的值

1、手肘法

手肘法的核心名額是SSE(sum of the squared errors，誤差平方和)，

S S E = ∑ i = 1 k ∑ p ∈ C i ∣ p − m i ∣ 2 S S E = \sum _ { i = 1 } ^ { k } \sum _ { p \in C _ { i } } \left| p - m _ { i } \right| ^ { 2 } SSE=i=1∑kp∈Ci∑∣p−mi∣2

其中， C i C_i Ci是第 i i i個簇， p p p是 C i C_i Ci中的樣本點， m i m_i mi是 C i C_i Ci的質心（ C i C_i Ci中所有樣本的均值），SSE是所有樣本的聚類誤差，代表了聚類效果的好壞。

手肘法的核心思想是：随着聚類數k的增大，樣本劃分會更加精細，每個簇的聚合程度會逐漸提高，那麼誤差平方和SSE自然會逐漸變小。并且，當k小于真實聚類數時，由于k的增大會大幅增加每個簇的聚合程度，故SSE的下降幅度會很大，而當k到達真實聚類數時，再增加k所得到的聚合程度回報會迅速變小，是以SSE的下降幅度會驟減，然後随着k值的繼續增大而趨于平緩，也就是說SSE和k的關系圖是一個手肘的形狀，而這個肘部對應的k值就是資料的真實聚類數。當然，這也是該方法被稱為手肘法的原因。

實踐：我們對預處理後資料.csv 中的資料利用手肘法選取最佳聚類數k。具體做法是讓k從1開始取值直到取到你認為合适的上限(一般來說這個上限不會太大，這裡我們選取上限為8)，對每一個k值進行聚類并且記下對于的SSE，然後畫出k和SSE的關系圖（毫無疑問是手肘形），最後選取肘部對應的k作為我們的最佳聚類數。python實作如下：

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
df_features = pd.read_csv(r'C:\預處理後資料.csv',encoding='gbk') # 讀入資料
'利用SSE選擇k'
SSE = []  # 存放每次結果的誤差平方和
for k in range(1,9):
    estimator = KMeans(n_clusters=k)  # 構造聚類器
    estimator.fit(df_features[['R','F','M']])
    SSE.append(estimator.inertia_)
X = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

畫出的k與SSE的關系圖如下：

K-means算法詳解及實作

顯然，肘部對于的k值為4，故對于這個資料集的聚類而言，最佳聚類數應該選4

2、輪廓系數法

該方法的核心名額是輪廓系數（Silhouette Coefficient），某個樣本點 X i X_i Xi的輪廓系數定義如下：

S = b − a max ⁡ ( a , b ) S = \frac { b - a } { \max ( a , b ) } S=max(a,b)b−a

其中， a a a是 X i X_i Xi與同簇的其他樣本的平均距離，稱為凝聚度（将 a a a稱為樣本 X i X_i Xi的簇内不相似度）， b b b是 X i X_i Xi與最近簇中所有樣本的平均距離，稱為分離度（将 b b b稱為樣本 X i X_i Xi的簇間不相似度的最小值）。

而最近簇的定義是：

C j = arg ⁡ min ⁡ C k 1 n ∑ p ∈ C k ∣ p − X i ∣ 2 C _ { j } = \arg \min _ { C _ { k } } \frac { 1 } { n } \sum _ { p \in C _ { k } } \left| p - X _ { i } \right| ^ { 2 } Cj=argCkminn1p∈Ck∑∣p−Xi∣2

其中 p p p是某個簇 C k C_k Ck中的樣本。事實上，簡單點講，就是用 X i X_i Xi到某個簇所有樣本的平均距離作為衡量該點到該簇的距離後，選擇離 X i X_i Xi最近的一個簇作為最近簇。

求出所有樣本的輪廓系數後再求平均值就得到了平均輪廓系數。平均輪廓系數的取值範圍為[-1,1]，且簇内樣本的距離越近，簇間樣本距離越遠，平均輪廓系數越大，聚類效果越好。那麼，很自然地，平均輪廓系數最大的k便是最佳聚類數。

實踐：我們同樣使用上面的資料集，同樣考慮 k k k等于 1 1 1到 8 8 8的情況，對于每個 k k k值進行聚類并且求出相應的輪廓系數，然後做出 k k k和輪廓系數的關系圖，選取輪廓系數取值最大的k作為我們最佳聚類系數，python實作如下：

import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
 
df_features = pd.read_csv(r'C:\Users\61087\Desktop\項目\爬蟲資料\預處理後資料.csv',encoding='gbk')
Scores = []  # 存放輪廓系數
for k in range(2,9):
    estimator = KMeans(n_clusters=k)  # 構造聚類器
    estimator.fit(df_features[['R','F','M']])
    Scores.append(silhouette_score(df_features[['R','F','M']],estimator.labels_,metric='euclidean'))
X = range(2,9)
plt.xlabel('k')
plt.ylabel('輪廓系數')
plt.plot(X,Scores,'o-')
plt.show()

得到聚類數k與輪廓系數的關系圖：

K-means算法詳解及實作

可以看到，輪廓系數最大的k值是2，這表示我們的最佳聚類數為2。但是，值得注意的是，從k和SSE的手肘圖可以看出，當k取2時，SSE還非常大，是以這是一個不太合理的聚類數，我們退而求其次，考慮輪廓系數第二大的k值4，這時候SSE已經處于一個較低的水準，是以最佳聚類系數應該取4而不是2。

但是，講道理，k=2時輪廓系數最大，聚類效果應該非常好，那為什麼SSE會這麼大呢？在我看來，原因在于輪廓系數考慮了分離度b，也就是樣本與最近簇中所有樣本的平均距離。為什麼這麼說，因為從定義上看，輪廓系數大，不一定是凝聚度a（樣本與同簇的其他樣本的平均距離）小，而可能是b和a都很大的情況下b相對a大得多，這麼一來，a是有可能取得比較大的。a一大，樣本與同簇的其他樣本的平均距離就大，簇的緊湊程度就弱，那麼簇内樣本離質心的距離也大，進而導緻SSE較大。是以，雖然輪廓系數引入了分離度b而限制了聚類劃分的程度，但是同樣會引來最優結果的SSE比較大的問題，這一點也是值得注意的。

3、總結

從以上兩個例子可以看出，輪廓系數法确定出的最優k值不一定是最優的，有時候還需要根據SSE去輔助選取，這樣一來相對手肘法就顯得有點累贅。是以，如果沒有特殊情況的話，我還是建議首先考慮用手肘法。

四、代碼實作

def kmeans(k):
    m, n = 100, 20  # 構造樣本：100行、20列（100個樣本，每個樣本20維特征）
    x = 10 * np.random.random((m, n))  # 0-1   x是訓練集，無标簽

    # 建立k個點作為初始中心點/質心（經常是随機選擇）
    init_cent_sample = set()  # 用set的原因是為了去重
    while len(init_cent_sample) < k:
        init_cent_sample.add(np.random.randint(0, m))  # [low, high)  # 中心點/質心 在這裡僅用其idx表示，後面還會處理

    # 儲存簇中心點（聚類中心點），k個聚類中心點（每個中心點都是一個n維的向量）
    cent_pos = x[list(init_cent_sample)]  # 第i個質心的坐标為：cent_pos[i]

    # 記錄每個樣本的類歸屬和（距離其所屬簇質心的）距離    [每個樣本所歸屬的簇中心點idx， 該樣本距離此簇中心點的距離]
    sample_belong_to = np.zeros((m, 2))  # np.array([min_idx, min_dist])

    # 記錄每個類的中心點在本次疊代後是否有過改變
    cent_changed = True
    # 當任意一個點的簇配置設定結果發生改變時
    while cent_changed:
        cent_changed = False

        # 對資料集中的每個樣本點
        for i in range(m):
            # 記錄每個樣本距離最近的類
            min_idx = -1
            # 記錄每個樣本的最小類距
            min_dist = math.inf

            # 對資料集中的每個資料點，計算其與k個質心的距離
            for j in range(k):
                d = distance(x[i], cent_pos[j])
                if d < min_dist:
                    min_idx = j
                    min_dist = d

            # 記錄此樣本（即第i個樣本）所對應的中心點是否發生變化（隻有所有樣本所歸屬的簇類中心點都不變時，才停止疊代）
            if min_idx != sample_belong_to[i][0]:
                sample_belong_to[i] = np.array([min_idx, min_dist])  # [每個樣本所歸屬的簇中心點idx， 該樣本距離此簇中心點的距離]
                cent_changed = True

        print(sample_belong_to)

        # 更新每個類/簇的中心點：均值
        for i in range(k):
            samples_of_curr_cluster = np.where(sample_belong_to[:, 0] == i)  # 隻有條件(condition)，沒有x和y，則輸出滿足條件（即非0）元素的坐标（等價于numpy.nonzero）。
            if len(samples_of_curr_cluster) > 0:
                print(samples_of_curr_cluster)
                cent_pos[i] = np.mean(x[samples_of_curr_cluster], axis = 0)


# 計算距離
def distance(a, b):
    return math.sqrt(sum(pow(a - b, 2)))

五、其他問題的解答

K-means算法中初始點的選擇對最終結果有影響嗎？

會有影響的，不同的初始值結果可能不一樣（選不好可能會得到局部最優）

K-means聚類中每個類别中心的初始點如何選擇？
- 随機法：最簡單的确定初始類簇中心點的方法是随機選擇K個點作為初始的類簇中心點。
- 這k個點的距離盡可能遠：首先随機選擇一個點作為第一個初始類簇中心點，然後選擇距離該點最遠的那個點作為第二個初始類簇中心點，然後再選擇距離前兩個點的最近距離最大的點作為第三個初始類簇的中心點，以此類推，直到選出k個初始類簇中心。
- 可以對資料先進行層次聚類（部落格後期會更新這類聚類算法），得到K個簇之後，從每個類簇中選擇一個點，該點可以是該類簇的中心點，或者是距離類簇中心點最近的那個點。

K-means中空聚類的處理
- 選擇一個距離目前任何質心最遠的點。這将消除目前對總平方誤差影響最大的點。
- 從具有最大SSE的簇中選擇一個替補的質心，這将分裂簇并降低聚類的總SSE。如果有多個空簇，則該過程重複多次。
- 如果噪點或者孤立點過多，考慮更換算法，如密度聚類（部落格後期會更新這類聚類算法）

K-means是否會一直陷入選擇質心的循環停不下來？

不會，有數學證明Kmeans一定會收斂，大概思路是利用SSE的概念（也就是誤差平方和），即每個點到自身所歸屬質心的距離的平方和，這個平方和是一個凸函數，通過疊代一定可以到達它的局部最優解。
- 疊代次數設定
- 設定收斂判斷距離

如何快速收斂資料量超大的K-means？

相關解釋可以去這個部落格稍做了解https://blog.csdn.net/sunnyxidian/article/details/89630815

K-means算法的優點和缺點是什麼？

K-Means的主要優點：

（1）原理簡單，容易實作

（2）可解釋度較強

K-Means的主要缺點：（對應改進和優化暫時還沒補充）

（1）K值很難确定

（2）局部最優

（3）對噪音和異常點敏感

（4）需樣本存在均值（限定資料種類）

（5）聚類效果依賴于聚類中心的初始化

（6）對于非凸資料集或類别規模差異太大的資料效果不好

K-Means與KNN有什麼差別

1）KNN是分類算法，K-means是聚類算法；

2）KNN是監督學習，K-means是非監督學習

如何對K-means聚類效果進行評估？

輪廓系數（Silhouette Coefficient），是聚類效果好壞的一種評價方式。最早由 Peter J. Rousseeuw 在 1986 提出。它結合凝聚度和分離度兩種因素。可以用來在相同原始資料的基礎上用來評價不同算法、或者算法不同運作方式對聚類結果所産生的影響。

em算法與k-means的關系，用em算法推導解釋k means

用hadoop實作看k means

如何判斷自己實作的 LR、Kmeans 算法是否正确？

References

https://blog.csdn.net/WangZixuan1111/article/details/98970139
https://blog.csdn.net/WangZixuan1111/article/details/98947683
https://blog.csdn.net/orangefly0214/article/details/86538865
https://mp.weixin.qq.com/s?__biz=Mzg2MjI5Mzk0MA==&mid=2247484061&idx=1&sn=2f9d5def9ec4615a9f4234c931124b92&chksm=ce0b5846f97cd150a479c37ee24f497ae864065415f23ca7f28f67206d949c718430f607919f&scene=21#wechat_redirect

K-means算法詳解及實作

文章目錄

一、原理和流程

1、原理

2、流程

二、K-means中常用的到中心距離的度量有哪些

三、K-means中的k值如何選取

1、手肘法

2、輪廓系數法

3、總結

四、代碼實作

五、其他問題的解答

References

繼續閱讀

Dropout深入了解

[機器學習筆記] （四）決策樹 Decision Tree

[機器學習] ModuleNotFoundError: No module named 'prettytable' 錯誤的解決

【關于時間序列的ML】項目 8 ：使用 Facebook Prophet 模型預測股票價格

【Seq2Seq】使用神經網絡進行序列到序列學習

【XGBoost】第 9 章：XGBoost Kaggle 大師探索 Kaggle 比賽工程新列建構不相關的集合堆疊模型概括

[機器學習筆記] 用Python分析：紅葡萄酒品質分析（資料探索）

[機器學習筆記] 機器學習中的“過拟合（Overfitting）”和“欠拟合（Underfitting）”

conda環境的複制（生成.yaml檔案）和pip環境的複制（生成requirements.txt）

pip自動生成和安裝requirements.txt