第四階段我們進行深度學習(AI),本部分(第一部分)主要是對底層的資料結構與算法部分進行詳盡的講解,通過本部分的學習主要達到以下兩方面的效果:
1.對開發中常見的算法能應用自如,讓你在跳槽找工作中“算法題”不再是阻礙你“錢途”的攔路虎。
2.我們不需要調參數的調參攻城獅,我們要做正真的自己的AI模型。
3.本部分預計40篇左右。
hello,大家好,今天我們來聊一個有點燒腦的資料結構--跳表,what? 跳表是個什麼鬼,且聽我慢慢道來。這裡先給大家說一下,今天的算法不強求大家一定能自己完全寫出來,但是整個思路得非常清晰
還記得我們上講說過的二分查找算法嗎,ok 你若還不是很清楚那建議你在看一下上一篇的文章,跳表:就是對連結清單稍加改造,就可以支援類似“二分”的查找算法。我們把改造之後的資料結構叫作跳表(Skip list)。
第一、如何了解跳表
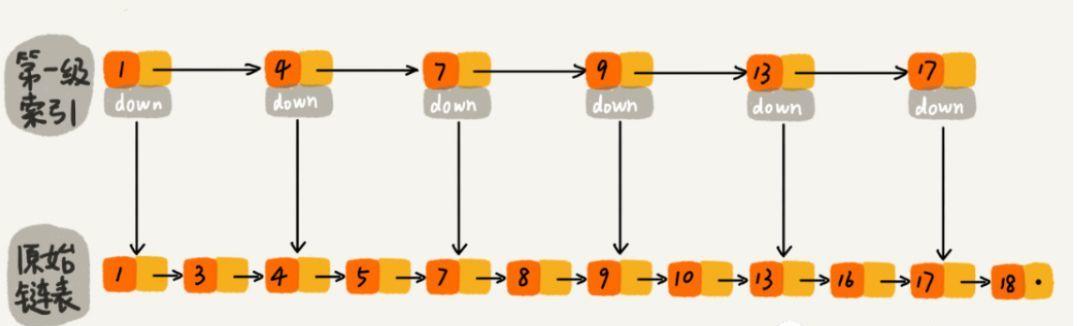
對于一個單連結清單來講,即便連結清單中存儲的資料是有序的,如果我們要想在其中查找某個資料,也隻能從頭到尾周遊連結清單。這樣查找效率就會很低,時間複雜度會很高,是 O(n)。 那怎麼來提高查找效率呢?如果像圖中那樣,對連結清單建立一級“索引”,查找起來是不是就會更快一些呢?每兩個結點提取一個結點到上一級,我們把抽出來的那一級叫作索引或索引層。你可以看我畫的圖。圖中的 down 表示 down 指針,指向下一級結點。
第二、跳表的資料結構實作
如何從代碼的層面來實作跳表呢?我們先看一張圖檔:
通過圖檔我們能很清楚的看到:每個節點都是有多個指針的,當然這個指針數的多少與建構的索引的層數是有關系的,最低層是包含所有的資料結點的。(其實質也是用空間換取時間的一種操作)。
第三、跳表查詢的效率
這個時間複雜度的分析方法比較難想到。我把問題分解一下,先來看這樣一個問題,如果連結清單裡有 n 個結點,會有多少級索引呢?
按照我們剛才講的,每兩個結點會抽出一個結點作為上一級索引的結點,那第一級索引的結點個數大約就是 n/2,第二級索引的結點個數大約就是 n/4,第三級索引的結點個數大約就是 n/8,依次類推,也就是說,第 k 級索引的結點個數是第 k-1 級索引的結點個數的 1/2,那第 k級索引結點的個數就是 n/(2k)。假設索引有 h 級,最進階的索引有 2 個結點。通過上面的公式,我們可以得到 n/(2h)=2,進而求得 h=log2n-1。如果包含原始連結清單這一層,整個跳表的高度就是 log2n。我們在跳表中查詢某個資料的時候,如果每一層都要周遊 m 個結點,那在跳表中查詢一個資料的時間複雜度就是 O(m*logn)。那這個 m 的值是多少呢?按照前面這種索引結構,我們每一級索引都最多隻需要周遊 3 個結點,也就是說 m=3,為什麼是 3 呢?我來解釋一下。
假設我們要查找的資料是 x,在第 k 級索引中,我們周遊到 y 結點之後,發現 x 大于 y,小于後面的結點 z,是以我們通過 y 的 down 指針,從第 k 級索引下降到第 k-1 級索引。在第 k-1 級索引中,y 和 z 之間隻有 3 個結點(包含 y和 z),是以,我們在 K-1 級索引中最多隻需要周遊 3 個結點,依次類推,每一級索引都最多隻需要周遊 3 個結點。
通過上面的分析,我們得到 m=3,是以在跳表中查詢任意資料的時間複雜度就是 O(logn)。這個查找的時間複雜度跟二分查找是一樣的。換句話說,我們其實是基于單連結清單實作了二分查找,是不是很神奇?不過,天下沒有免費的午
餐,這種查詢效率的提升,前提是建立了很多級索引,用空間換時間的設計思路。
第四、跳表的代碼實作(python版本)
由于本篇的代碼較多,不便于放于文中,如果感興趣,可以通過我提供的連結擷取。
好的,本期我們對于跳表算法就算就說完了,如果有問題可以進行留言。
由于代碼倉庫出現一些小問題,後續後把代碼傳上去的。
有小夥伴在背景留言,說能不能推一些關于python面試方面的資料呢,這個已近在考慮之中了,很快就會上線第一季的,敬請期待哈