B樹
B樹即平衡查找樹,一般了解為平衡多路查找樹,也稱為B-樹、B_樹。是一種自平衡樹狀資料結構,能對存儲的資料進行O(log n)的時間複雜度進行查找、插入和删除。B樹一般較多用在存儲系統上,比如資料庫或檔案系統。
B樹特點
- B樹可以定義一個m值作為預定範圍,即m路(階)B樹。
- 每個節點最多有m個孩子。
- 每個節點至少有ceil(m/2)個孩子,除了根節點和葉子節點外。
- 對于根節點,子樹個數範圍為[2,m],節點内值的個數範圍為[1,m-1]。
- 對于非根節點,節點内的值個數範圍為[ceil(m/2)-1,m-1]。
- 根節點(非葉子節點)至少有兩個孩子。
- 一個有k個孩子的非葉子節點包含k-1個值。
- 所有葉子節點在同一層。
- 節點内的值按照從小到大排列。
- 父節點的若幹值作為分離值分成多個子樹,左子樹小于對應分離值,對應分離值小于右子樹。
以下是一個四階B樹,
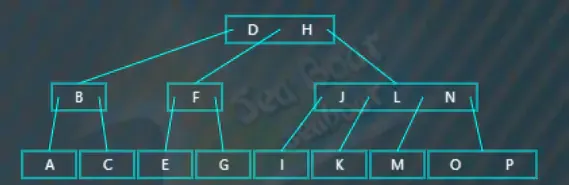
插入
假設現在建構一棵四階B樹,開始插入“A”,直接作為根節點,
插入“B”,大于“A”,放右邊,
插入“C”,按順序排到最後,
繼續插入“D”,直接添加的結果如下圖,此時超過了節點可以存放容量,對于四階B樹每個節點最多存放3個值,此時需要執行分裂操作,
分裂操作為,先選取待分裂節點的中值,這裡為“B”,然後将中值“B”放到父節點中,因為這裡還沒有父節點,那麼直接建立一個新的父節點存放“B”,而原來小于“B”的那些值作為左子樹,原來大于“B”的那些值作為右子樹。
繼續插入“E”,"E"大于“B”,往右子節點,
分别于“C”和“D”比較,大于它們,放到最右邊,
插入“F”,“F”大于“B”,往右子樹,
“F”分别與“C”“D”"E"比較,大于它們,放到最右邊,此時觸發分裂操作,
選取待分裂節點的中值“D”,然後将中值“D”放到父節點中,父節點中的“B”小于“D”,于是放到“B”右邊,而原來小于“D”的那些值作為左子樹,原來大于“D”的那些值作為右子樹。
繼續插入“M”,結果為,
插入“L’,大于“B”“D”,往右子樹,
“L”大于“E”“F”小于“M”,于是放到第三個位置,此時觸發分裂操作,
選取待分裂節點的中值“F”,然後将中值“F”放到父節點中,父節點中的“B”“D”都小于“F”,于是放到最右邊,而原來小于“F”的那些值作為左子樹,原來大于“F”的那些值作為右子樹。
插入“K”,結果為,
插入“J”,大于“B”“D”“F”,往右子樹,
“J”小于“K”“L”“M”,于是放到第一個位置,此時觸發分裂操作,
選取待分裂節點的中值“K”,然後将中值“K”放到父節點中,父節點中的“B”“D”“F”都小于“K”,于是放到最右邊,而原來小于“K”的那些值作為左子樹,原來大于“K”的那些值作為右子樹。此時父節點也觸發分裂操作,
選取待分裂節點的中值“D”,然後将中值“D”放到父節點中,由于還沒有父節點,那麼直接建立一個新的父節點存放“D”,而原來小于“D”的那些值作為左子樹,原來大于“D”的那些值作為右子樹。
插入“I”,大于“D”,往右子樹,
右子樹不是葉子節點,繼續往下,這時“I”大于“F”而小于“K”,是以往第二個分支,
“I”小于“J”,于是放到左邊,
類似地,插入“H”,結果如下,
插入“G”,往左子樹,
往中間分支,
觸發分裂操作,
選取待分裂節點的中值“H”,然後将中值“H”放到父節點中,"H"大于父節點中的“F”而小于“K”,于是放到中間,而原來小于“H”的那些值作為左子樹,原來大于“H”的那些值作為右子樹。
綜上所述,插入操作的核心是分裂操作。無需分裂的情況比較簡單,直接插入即可;如果插入後超過節點容量,這個容量可預先自定義,則需要進行分裂操作,需要注意的是分裂可能引起父節點需要繼續分裂。
查找
對B樹進行查找就比較簡單,查找過程有點類似二叉搜尋樹,從根節點開始查找,根據比較數值找到對應的分支,繼續往子樹上查找。
比如查找“I”,"I"大于“D”,往右子樹,
“I”分别與節點内值比較,大于“F”“H”而小于“K”,往第三個分支,
逐一比較節點内的值,找到“I”。