1.最小二乘法
通過最小化誤差的平方,尋找資料的最佳函數比對。
通俗來說,我們有一些組資料,但是我們不知道這些資料之間的對應關系是什麼(一個公式),我們可以利用最小二乘方法,求出偏差最小時,我們的公式表達方式,即公式的未知參數。
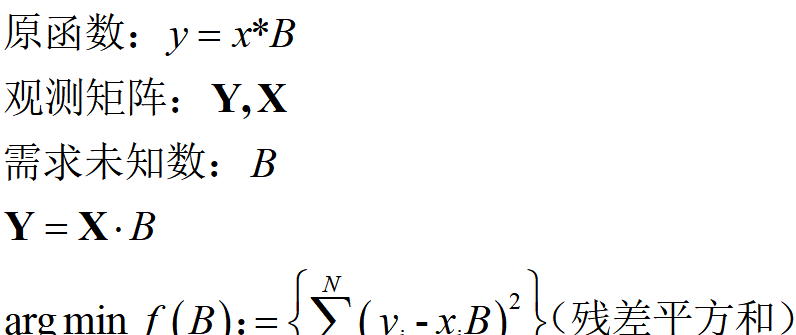
這裡可能有人會有疑問,什麼是觀測矩陣?
從字面了解為看到的矩陣,實際上是我們在測量時,得到的真實資料。例如我們需要标定一個系統的一些參數,我們隻需要為系統輸入一些變量,然後觀察得到的結果,最後利用最小二乘求出能表達系統的矩陣。
當然,有人還會聯想到,我們的線性公式很多是y=Bx+b,b去哪了?有了b,還能這樣求解麼?
這也是為什麼最小二乘時,建議左右均減去一個平均數,這樣b就可以消掉了。
當然消掉b隻是一方面,它是可以直接消掉一些單獨的不變未知參數的,這個可以在實際應用中發現這種方法的妙用。
到了這裡,大家也會去想,我如何找到我需求的B呢?
窮舉法,算出最小殘差平方和時的B………………這個最初是這樣做的,但是有點太浪費計算資源了,速度比較慢。
還有其他方法:(梯度下降法、牛頓法、拟牛頓法、共轭梯度法等)
2.矩陣表示求解問題
我們的方程以及觀測值都可以用矩陣來表示,用矩陣表示後,一些優化方法自然也可以放到矩陣下表示。
我們在用矩陣求最小二乘時,可能會有一個非常大的疑問。
一個矩陣的逆,乘上一個什麼,然後就直接解決了窮舉和最小二乘兩個步驟的工作。。。。
大家會很奇怪,我就把矩陣變化一下,就有這麼神奇????!!!!!
不然,不然,其實你把大部分計算都壓縮到了求逆的過程中了,而求逆你隻是寫了個求逆符号,具體怎麼求,你卻不會去管,也感覺自己不懂如何求的,隻是知道很友善。
是以,用矩陣求最小二乘,并不是很神奇,隻用矩陣變換就解決問題,而是在逆中解決了大量的問題,如何求逆,才是矩陣求最小二乘的精華,而這個精華,多數程式都提供了完備的解決方案,不需要使用者考慮。就像,你沒用矩陣之前,用最小二乘的時候還需要計算最小二乘和選擇最優的優化方案,當你用到矩陣的逆後在,這些操作都被計算機自己實作了。
這裡,還有另一個知識點。
我們大部分求逆時,隻是為了解方程,而并不是為了得到逆的顯式表示。
是以,我們隻需要在matlab中使用反斜杠運算符 \ ——高斯消去法
反斜杠計算方法速度更快,而且殘差減少了幾個數量級,快2-3倍。
如果A是方陣,A\B近似等于inv(A)*B,他們的不同之處在于算法。