OO第一單元總結
1. 基于度量來分析自己的程式架構
- 第一次作業
- 第一次作業為簡單多項式的求導,我的設計由SimplePoly, ComuptePoly類組成。ComputePoly通過正則比對單個項,并将其送入SimplePoly中進行合并構造形如a*x^b的簡單項,ComputePoly中定義簡單項構成的Arraylist。求導時,對每一項調用SimplePoly的deriv()方法,傳回其導數項,存儲在一個新的Arraylist中。最終對此Arraylist合并同類項,并逐項調用SimplePoly的toString方法輸出。
- 類圖
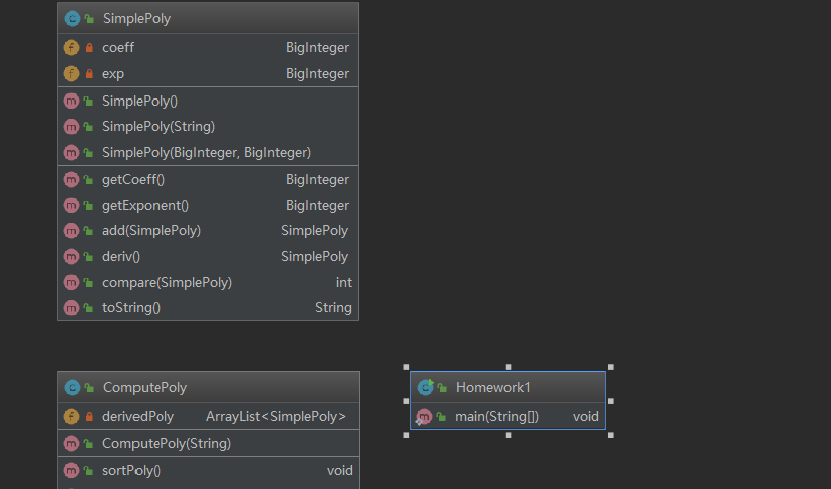
OO第一單元總結OO第一單元總結 - 複雜度
OO第一單元總結OO第一單元總結
- 第二次作業
- 第二次作業增加了簡單三角函數sin(x)和cos(x),我的設計如下
- 簡單函數類:Cosine,Sine, Power 分别定義由字元串作為參數的構造器方法,傳回字元串的求導方法deriv(), 傳回字元串的toString()
- Item: 執行個體域由前述的三個簡單函數對象及Biginteger型系數組成,接受由加減号作為分割的字元串類型的項作為參數,通過正則解析并送至底層函數類。deriv()方法用于求導: 對形如u*v*w的三個對象的乘積,分别調用他們的deriv() 和toString(),得到字元串類型的三項之和,将這三項分别通過Item的構造器執行個體化,并存儲在一個Arraylist中傳回。
- Poly: 定義由Item組成的Arraylist: allItem,通過正則對表達式進行拆分,得到的每一項通過送入Item類構造,求導時,周遊allItem,調用Item的deriv()方法,得到其導數組成的arraylist。
- 類圖
OO第一單元總結OO第一單元總結 - 複雜度
OO第一單元總結OO第一單元總結
- 第二次作業增加了簡單三角函數sin(x)和cos(x),我的設計如下
- 第三次作業
- 思路:第三次作業在第二次作業的基礎上增加了表達式因子,并允許因子嵌套在三角函數因子裡面,對此,我增加了factor類作為簡單函數類的父類,并在Sine,Cosine類中定義Expression類型的selfVar作為它的自變量,求導時通過遞歸進行。
- 類圖
OO第一單元總結OO第一單元總結 - 複雜度
OO第一單元總結OO第一單元總結
2. 分析自己程式的bug
- 第一次作業:在用正則進行拆項之前調用了String.trim()方法,導緻對于表達式開頭或結尾的非法空白字元無法識别
- 第二次作業:在化簡結果時,為縮短表達式長度,将正項提前,但我在周遊尋找正項之後,忘記判斷是否含有正項,導緻當表達式的導數隻有負項時程式出現IndexOutOfBoundsException
- 第三次作業:本次作業由于我沒有對結果進行化簡,并且對所有的表達式強制添加括号,在強側和互測階段均未發現bug, 但輸出結果又臭又長,并且幾乎毫無擴充性。
3. 分析自己發現别人程式bug所采用的政策
- 通過各個層次表達式的形式,構造正确的表達式測試集,并在此測試集上稍作改動構造非法測試集
- 通過調試,觀察其他同學處理表達式的大緻步驟,重點讀構造器部分
4. Applying Creational Pattern
第三次作業毫無擴充性,且各級求導方法均傳回字元串,應該将輸入與化簡輸出單獨封裝。
轉載于:https://www.cnblogs.com/okawaikoto/p/10610560.html