主成分分析(Principal Components Analysis, PCA)是最重要的降維方法之一,在資料壓縮、消除備援和資料噪音消除等方面有廣泛的應用。通常我們提到降維算法,最先想到的就是PCA,下面我們對PCA原理進行介紹。
1. PCA思想
PCA就是找出資料中最主要的方面,用資料中最重要的方面來代替原始資料。假如我們的資料集是n維的,共有m個資料(x1,x2,...,xm),我們将這m個資料從n維降到r維,希望這m個r維的資料集盡可能的代表原始資料集。
我們知道從n維降到r維肯定會有損失,但是希望損失盡可能的小,那麼如何讓這r維的資料盡可能表示原來的資料呢?首先來看最簡單的情況,即将二維資料降到一維,也就是n=2,r=1。資料如下圖所示,我們希望找到某一個次元方向,它可以代表這兩個次元的資料。圖中列了兩個向量,也就是u1和u2,那麼哪個向量可以更好的代表原始資料集呢?
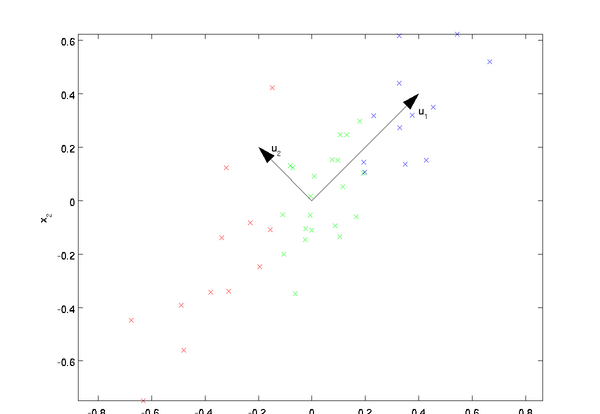
直覺上看u1比u2更好,為什麼呢?可以有兩種解釋,第一種解釋是樣本點在這個直線上的投影盡可能的分開,第二種解釋是樣本點到這個直線的距離足夠近。假如我們把r從1維推廣到任意維,則我們希望降維的标準為樣本點在這個超平面上的投影盡可能分開,或者說樣本點到這個超平面的距離足夠近。基于上面的兩種标準,我們可以得到PCA的兩種等價推導。
2. PCA推導:基于最大投影方差
2.1 基變換
一般來說,想要獲得原始資料的表示空間,最簡單的方式是對原始資料進行線性變換(基變換),即Y=PX。其中Y是樣本在新空間的表達,P是基向量,X是原始樣本。我們可知選擇不同的基能夠對一組資料給出不同的表示,同時當基的數量少于原始樣本本身的維數時,則可以達到降維的效果,矩陣表示如下
2.2 方差
那麼考慮,如何選擇一個方向或者基才是最優的呢? 觀察上圖,我們将所有的點分别向兩條直線做投影,基于前面PCA最大可分的思想,我們要找的方向是降維後損失最小,可以了解為投影後的資料盡可能的分開。那麼這種分散程度可以用數學上的方差進行表示,方差越大資料越分散,方差公式如下所示
對資料進行中心化後得到
現在我們知道以下幾點
- 對原始資料進行基變換可以對原始資料給出不同表示。
- 基的次元小于資料的次元可以起到降維的效果。
- 對基變換後新的樣本進行求方差,選擇使其方差最大的基。
2.3 協方差
基于上面提到的幾點,我們來探讨如何尋找計算方案。從上面可以得到,二維降到一維可以使用方差最大,來選出能使基變換後資料分散最大的方向(基),但如果遇到高維的變換,怎麼辦呢?
針對高維情況,數學上采用協方差來表示
2.4 協方差矩陣
2.5 協方差矩陣對角化
我們來看看原資料協方差矩陣和通過基變換後的協方差矩陣之間的關系。設原資料協方差矩陣為C,P是一組基按行組成的矩陣,設Y=PX,則Y為X對P做基變換後的資料。設Y的協方差矩陣為D,我們來推導一下D和C的關系
可以看出,我們的目标是尋找能夠讓原始協方差矩陣對角化的P。換句話說,優化目标變成了尋找一個矩陣P,滿足PCP^T是一個對角矩陣。并且對角元素按照從大到小依次排列,那麼P的前k行就是要尋找的基,用P的前k行組成的矩陣乘以X就使得X從n維降到了r維。
我們希望投影後的方差最大化,于是優化目标為
其中tr表示矩陣的迹,利用拉格朗日函數可以得到
對P進行求導,整理得到
3. PCA推導:基于最小投影距離
可以發現,和第二節基于最大投影方差的優化目标完全一樣。隻是上述計算的是加負号的最小化,現在計算的是無負号最大化。然後利用拉格朗日函數可以得到
對P求導有
4. PCA算法流程
5. 核主成分分析KPCA
在上面的PCA算法中,我們假設存在一個線性的超平面,可以讓我們對資料進行投影。但是有些時候,資料不是線性的,不能直接進行PCA降維。這裡便需要利用和支援向量機一樣的核函數思想,先把資料集從n維映射到線性可分的高維N,其中N>n,然後再從N維降維到一個低次元r,這裡次元之間滿足r
使用核函數的主成分分析稱為核主成分分析(Kernelized PCA, KPCA)。假設高維空間的資料由n維空間的資料通過映射ϕ産生。則對于n維空間的特征分解
映射為
通過在高維空間進行協方差的特征值分解,然後用和PCA一樣的方法進行降維。一般來說,映射ϕ不用顯式的計算,而是在需要計算的時候通過核函數完成。由于KPCA需要核函數的運算,是以它的計算量要比PCA大很多。
6. PCA算法總結
作為一個非監督學習的降維方法,PCA隻需要特征值分解,就可以對資料進行壓縮,去噪。是以在實際場景應用很廣泛。為了克服PCA的一些缺點,出現了很多PCA的變種,比如解決非線性降維的KPCA,還有解決記憶體限制的增量PCA方法Incremental PCA,以及解決稀疏資料降維的PCA方法Sparse PCA等。
你看到的這篇文章來自于公衆号「謂之小一」,歡迎關注我閱讀更多文章。