一、多目标粒子群算法簡介
1 算法提出
雖然PSO算法在許多單目标優化問題中的成功應用說明了PSO算法的有效性.但是PSO算法不能直接應用于多目标優化問題, 因為多目标優化問題和單目标優化問題是有本質的差別的:前者一般是一組或幾組連續解的集合, 而後者隻是單個解或一組連續的解.另外, 遺傳算法在多目标優化問題中的成功應用以及PSO算法和遺傳算法的相似性, 說明PSO算法可能是一種處理多目标優化問題方法.但PSO算法和遺傳算法還是有很大的不同:在遺傳算法中染色體間共享資訊, 是整個群體逐漸移向好的區域, 而PSO算法中資訊是由最好的粒子給出的, 其他個體跟着最好粒子快速向一點收斂.是以直接用PSO算法處理多目标優化問題, 将很容易收斂于非劣最優域的局部區域.
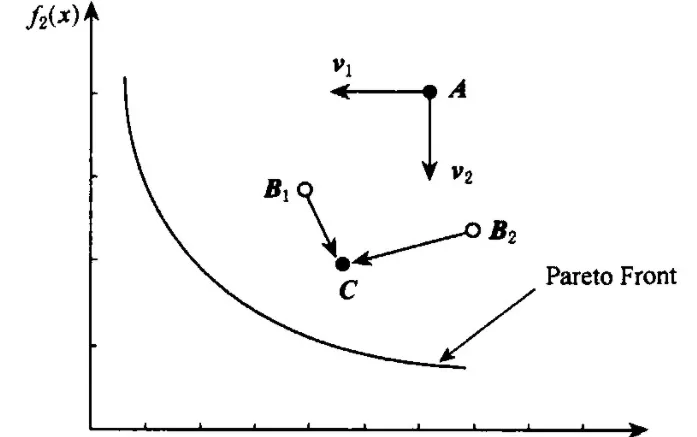
圖1 目标函數空間
基于以上原因, 本文提出了最優解評估選取的PSO算法, 用于對多目标優化問題的非劣最優解集的搜尋.算法在決策變量空間初始化一個粒子群, 通過多目标優化問題中的各個目标函數來共同指導粒子在決策變量空間中的飛行, 使其最終能落入非劣最優解集中;反映到目标函數空間, 粒子将落入非劣最優目标域.如圖1為極小化f1 (x) , f2 (x) 時目标函數空間中情況.如果隻有目标函數f1 (x) 或f2 (x) , 目标向量A将沿着v1或v2方向變化, 而算法中目标函數f1 (x) , f2 (x) 通過決策變量空間的粒子共同指導A的變化, 是以A既不沿v1方向變化, 也不沿v2方向變化, 而是從v1, v2間某一f1 (x) , f2 (x) 不同時增大的方向變化, 最終到達非劣最優目标域.具體通過下述方式實作:首先, 用多目标優化問題中的各個目标函數, 找到每個粒子對應于各個目标函數的全局極值gBest[i] (其中, i=1, 2, …, n是目标函數的個數) 和個體極值pBest[i, j] (其中, j=1, 2, …, N是粒子個數) .其次, 在更新每個粒子的速度時, 用各個gBest[i]的“均值”作為全局極值gBest;每個粒子的pBest[i, j]是通過判斷pBest[i, j]相對于gBest[i]的離散程度決定是取pBest[i, j]的均值還是在pBest[i, j]中随機選取.
2 算法分析
因為在PSO算法中每個粒子的行為主要由gBest和pBest決定, 是以本文的選取方式使得每個粒子向解移動時的行為各不相同:每個粒子都移向解區域中不同的解.這樣最終整個群體将分散于非劣最優解集中, 避免了收斂于非劣最優解集的局部區域.gBest的評估選取在避免了所有個體落于某一目标函數的最優點的同時, 更重要是展現了各個目标函數間的制約關系, 而pBest的選取方式更加強了這一行為.
如圖2為極小化f1 (x) , f2 (x) 時某次循環後決策變量空間中情況.群體對目标函數f1 (x) 而言的最好解為x1 (gBest[1]) , x2為f2 (x) 的最好解gBest[2].對應于x1, x2在目标函數空間的目标向量為B1, B2 (如圖1) .依據算法對gBest[1], gBest[2]評估選取得到gBest, 對應的解一定會在x1, x2之間, 假設為x0 (如圖2) , 而在目标函數空間與x0對應的目标向量為C.顯然C要比B1, B2更接近非劣最優目标域, 這也說明用x0 (gBest) 更新粒子要比用gBest[1]或gBest[2]更好.和标準的PSO算法相比, 本文是對粒子的全局極值和個體極值的選取做了改進.
圖2 決策變量空間
3 算法流程
下面以兩目标函數 (極小化f1 (x) , f2 (x) ) 優化為例給出算法流程 (沒有給出對粒子的每個次元的操作, 實際使用時可參考PSO算法的公式進行) .
① 初始化粒子群:給定群體規模N, 随機産生每個粒子的位置Xi、速度Vi.
② 用目标函數f1 (x) , f2 (x) 分别計算每個粒子的适應度值:
For i=1 to N
Fitness1[i]=f1 (X[i]) ;
Fitness2[i]=f2 (X[i]) ;
Next i
③ 在兩個目标函數f1 (x) , f2 (x) 下分别對每個粒子求得個體極值:
For i=1 to N
pBest[1, i]←f1 (x) ;
pBest[2, i]←f2 (x) ;
Next i
④ 對兩個目标函數f1 (x) , f2 (x) 分别求兩個全局極值:
gBest[1]←f1 (x) ;
gBest[2]←f2 (x) ;
⑤ 計算兩全局矢量的均值gBest和距離dgBest:
gBest=Average (gBest[1], gBest[2]) ;
dgBest=Distance (gBest[1], gBest[2]) ;
⑥ 計算每個粒子pBest[1, i]和pBest[2, i]之間的距離dpBest[i]:
For i=1 to N
dpBest[i]=Distance (pBest[1, i],
pBest[2, i]) ;
Next i
⑦ 對每個粒子計算更新速度Vi和位置Xi時所要用的個體極值pBest[i]:
⑧ 用⑤⑦所得的gBest和pBest[i]更新每個粒子速度Vi和位置Xi;
⑨ 如滿足中止條件, 退出, 否則傳回②.
說明:函數Average () 既可以是平均也可以是按一定比例動态選取.
二、部分源代碼
三、運作結果
四、matlab版本及參考文獻
1 matlab版本
2014a
2 參考文獻
[1] 包子陽,餘繼周,楊杉.智能優化算法及其MATLAB執行個體(第2版)[M].電子工業出版社,2016.
[2]張岩,吳水根.MATLAB優化算法源代碼[M].清華大學出版社,2017.