一、什麼是二叉搜尋樹
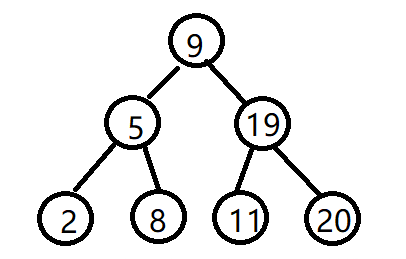
二叉搜尋樹本質還是二叉樹,但它在不空時添加節點,它左子樹上所有的元素都小于根節點的元素,而根節點右子樹上所有的元素都大于根節點的元素。
通過以上方法建的樹的中序周遊是從小到大的序列,是以二叉搜尋樹又稱之為二叉排序樹。
二、二叉搜尋樹的基本操作
2.1二叉搜尋樹插入節點
由于二叉搜尋樹仍然是二叉樹,是以先建立二叉樹類
public class tree {
private Object data;
private tree left;
private tree right;
public tree (){}
public tree(Object data) {
this.data = data;
}
public Object getData() {
return data;
}
public void setData(Object data) {
this.data = data;
}
public tree getLeft() {
return left;
}
public void setLeft(tree left) {
this.left = left;
}
public tree getRight() {
return right;
}
public void setRight(tree right) {
this.right = right;
}
}
接下來就是如何在二叉搜尋樹中添加節點
1.非遞歸的方式添加節點
(1)思路首先建立一個二叉樹,如果根節點為空,則将建立的二叉樹位址傳給跟根節點。如果不為空進行(2)
(2)建立臨時節點取得根節點,當臨時節點不為空時,判斷根節點和目前建立的樹要比較值的大小(這裡建立的二叉樹儲存的值的類型為Object,是以取出的資料需要連接配接Comparalbe接口),如果新節點小于目前節點,那麼進行(3),如果新節點不小于目前節點,進行(4)
(3)判斷臨時節點的左子樹是否為空,如果為空将新節點設定為臨時節點的左子樹,添加完畢退出循環。如果不為空,臨時節點指向它的左子樹,傳回(2)
(4)判斷臨時節點的右子樹是否為空,如果為空将新節點設定為臨時節點的右子樹,添加完畢退出循環。如果不為空,臨時節點指向它的右子樹,傳回(2)
public void add (Object data){
tree t = new tree(data);
if(root == null){
root = t;
}else {
tree temp = root;
while(temp!=null){
Comparable comparable =(Comparable)temp.getData();
if(comparable.compareTo(data)==1){
if(temp.getLeft()!=null)
temp = temp.getLeft();
else {
temp.setLeft(t);
break;
}
}
else {
if (temp.getRight() != null)
temp = temp.getRight();
else {
temp.setRight(t);
break;
}
}
}
}
this.size++;
}
2.遞歸的方式添加節點
思路:
(1)思路首先建立一個二叉樹,如果根節點為空,則将建立的二叉樹位址傳給跟根節點。如果不為空進行(2)
(2)建立函數f(tree currentNode,tree newNode) 兩個參數表示目前臨時節點和新節點。将這兩個節點進行比較如果新節點小于目前節點,那麼進行(3),如果新節點不小于目前節點,進行(4)
(3)判斷目前節點的左子樹是否為空,如果為空将新節點設定為臨時節點的左子樹,添加完畢。如果不為空,調用f(tree currentNode,tree newNode) 将目前currentNode修改為currentNode.getLeft().
(4)判斷臨時節點的右子樹是否為空,如果為空将新節點設定為臨時節點的右子樹,添加完畢。如果不為空,如果不為空,調用f(tree currentNode,tree newNode) 将目前currentNode修改為currentNode.getRight().
public void diguiAdd(Object data){
boolean flag = false;
tree node = new tree(data);
if(root == null){
root = node;
}
else{
flag = f(this.root,node);
}
if(!flag)
this.size++;
}
private boolean f(tree currentNode,tree newNode){
Comparable c = (Comparable) currentNode.getData();
Comparable n = (Comparable) newNode.getData();
if(c.compareTo(n) == -1){
if(currentNode.getRight() != null){
f(currentNode.getRight(),newNode);
}else{
currentNode.setRight(newNode);
}
}else if(c.compareTo(n) == 1){
if(currentNode.getLeft() != null){
f(currentNode.getLeft(),newNode);
}else{
currentNode.setLeft(newNode);
}
}else {
return true;
}
return false;
}
2.2二叉排序樹的查找算法
思路:
如果目前節點小于target則向目前節點的右節點前進,如果右節點不存在說明沒有這個target傳回null;
如果目前節點大于target則向目前節點的左節點前進,如果左節點不存在說明沒有這個target傳回null;
public Object get(Object data){
if(root == null){
return null;
}else {
tree temp = root;
while(temp!=null){
Comparable comparable =(Comparable)temp.getData();
if(comparable.compareTo(data)==1){
if(temp.getLeft()!=null)
temp = temp.getLeft();
else {
return null;
}
}
else if(comparable.compareTo(data)==-1){
if (temp.getRight() != null)
temp = temp.getRight();
else {
return null;
}
}else{
if(data.equals(temp.getData())) // data需要重寫equals方法
return temp.getData();
else return null;
}
}
}
return null;
}
2.3在二叉排序樹删除結點的算法
删除節點有三種情況
(1)需要删除的節點左子樹和右子樹為空
此時可以直接将這個節點指空,最後傳回空,使這個節點的父節點的子樹設為空。
(2)如圖所示,需要删除的節點左子樹或者右子樹為空,此時将現在的節點指向它的左子樹(如果左子樹為空則指向右子樹)。
(3)如圖所示,需要删除的節點的左右子樹均存在,此時需要将左右子樹中節點值跟它最接近的節點,變成此節點,這裡取最接近它比他大的節點,也就是此節點右子樹最深的左子樹,也就是圖中的10,然後調用删除節點的算法遞歸将子樹15中的10删除
public void remove(Object data){
this.root = deleteNode(this.root,data);
if(size>0)
size--;
}
public tree deleteNode(tree root , Object data){
if(root == null) return null;
Comparable comparable = (Comparable) root.getData();
if(comparable.compareTo(data)==1)
root.setLeft(deleteNode(root.getLeft(),data));
else if(comparable.compareTo(data)==-1)
root.setRight(deleteNode(root.getRight(),data));
else{
if(root.getLeft()==null||root.getRight()==null){
tree temp = root.getLeft()!=null ? root.getLeft():root.getRight();
if(temp == null){
temp = root;
root = null;
}else{
root = temp;
temp =null;
}
}else{
tree temp = minValueNode(root.getRight());
root.setData(temp.getData());
root.setRight(deleteNode(root.getRight(),temp.getData()));
}
}
if(root == null)
return root;
return root;
}
public tree minValueNode(tree Node){
tree cur = Node;
while(cur.getLeft()!=null){
cur = cur.getLeft();
}
return cur;
}
删除算法測試
完整代碼
https://github.com/yhq915540781/javaPra/blob/master/src/Algorithm/dataStructure/searchBinaryTree.java
三、二叉排序樹性能分析
由于所要查找的資料量不同,則其查找的性能也不同。且二叉排序樹的平均查找長度與樹的形态有關。最好情況是:二叉排序樹和二叉判定樹形态相同;最壞情況是:二叉排序為單支樹,則其平均查找長度與順序查找相同。