Climbing Stairs（爬樓梯）

題目描述（Easy）

假設一個樓梯有n梯，每次隻能爬1梯或2梯，求出有多少種爬的方式。

注意：給定n是一個正整數。

樣例

示例 1：

輸入： 2
輸出： 2
解釋： 有兩種方法可以爬到樓頂。
1.  1 步 + 1 步
2.  2 步      

示例 2：

輸入： 3
輸出： 3
解釋： 有三種方法可以爬到樓頂。
1.  1 步 + 1 步 + 1 步
2.  1 步 + 2 步
3.  2 步 + 1 步      

題目連結

Climbing Stairs（爬樓梯）

方法思路

第一直覺

遞歸：f(n) = f(n - 1) + f(n - 2)。但太慢，因為會重複計算很多次f(k)(k <= n)。

變量記錄方式

1、考慮preNumDistinctWays記錄前一梯的方法數；

2、令目前方法數distinctWays，加上前一梯preNumDistinctWays方法數，就是下一梯求的方法數；distinctWays+= preNumDistinctWays。

通項公式

另外，菲波拉契數列也有通項公式：

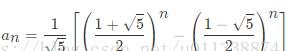
核心代碼

public int climbStairs(int n) {
        // 前一梯的方法數
        int preNumDistinctWays = 0;
        // 求的總方法數
        int distinctWays = 1;
        for (int i = 1; i <= n; i++) {
            // 未加之前方法數臨時變量
            int temp = distinctWays;
            // 目前方法數 += 前一梯方法數
            distinctWays += preNumDistinctWays;
            // 将臨時變量指派給前一梯方法數變量
            preNumDistinctWays = temp;
        }
        return distinctWays;
    }