Radar Installation（POJ-1328）

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

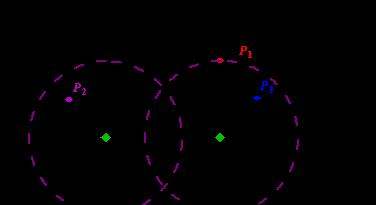
Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.

The input is terminated by a line containing pair of zeros

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0
      

Sample Output

Case 1: 2
Case 2: 1
      

題意：海上有很多島嶼，每個島嶼都給你坐标，讓你在x軸上（相當于海岸線）放置雷達，最少放幾個；

思路：貪心，把每個島嶼放置雷達的區間求出來，沿途比較就行；

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define INF 0x3f3f3f3f
#define maxn 1010
using namespace std;
struct edge
{
    double l,r;
};
edge g[maxn];
bool cmp(edge a,edge b)
{
    return a.l<b.l;
}
double x,y;
int n,d,t;
int main()
{
    t=0;
    while(scanf("%d%d",&n,&d)!=EOF){
        if(n==0&&d==0) break;
        t++;
        bool flag=true;
        for(int i=0;i<n;i++){
            scanf("%lf%lf",&x,&y);
            if(y>d) flag=false;
            g[i].l=x-sqrt(1.0*d*d-y*y);
            g[i].r=x+sqrt(1.0*d*d-y*y);
        }
        printf("Case %d: ",t);
        if(!flag){
            cout<<-1<<endl;
            continue;
        }
        sort(g,g+n,cmp);
        double xx=g[0].r;
        int sum=1;
        for(int i=1;i<n;i++){
            if(g[i].r<xx) xx=g[i].r;
            else if(g[i].l>xx){
                sum++;
                xx=g[i].r;
            }
        }
        cout<<sum<<endl;
    }
}