Java實作最小堆二

Java實作最小堆二

如何建立這個堆呢，可以從空的堆開始，然後依次往堆中插入每一個元素，直到所有數都被插入。

因為插入第N個元素的所用的時間是O(logN)，是以插入所有元素的整體時間複雜度是O(NlogN)，代碼如下。

n=0;
for(i=1;i<=m;i++)
{
    n++;
    h[n]=a[i];  //或者寫成scanf("%d",&h[n]);
    siftup();
}

           

其實我們還有更快得方法來建立堆。它是這樣的，直接把99、5、36、7、22、17、46、12、2、19、25、28、1和92這14個數放入一個完全二叉樹中（這裡我們還是用一個一維數組來存儲完全二叉樹）。

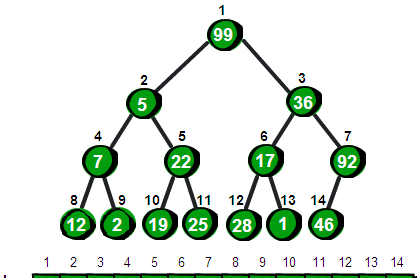
在這個棵完全二叉樹中，我們從最後一個結點開始依次判斷以這個結點為根的子樹是否符合最小堆的特性。如果所有的子樹都符合最小堆的特性，那麼整棵樹就是最小堆了。如果這句話沒有了解不要着急，繼續往下看。

首先我們從葉結點開始。因為葉結點沒有兒子，是以所有以葉結點為根結點的子樹（其實這個子樹隻有一個結點）都符合最小堆的特性（即父結點的值比子結點的值小）。這些葉結點壓根就沒有子節點，當然符合這個特性。是以所有葉結點都不需要處理，直接跳過。從第n/2個結點（n為完全二叉樹的結點總數，這裡即7号結點）開始處理這棵完全二叉樹。注意完全二叉樹有一個性質：最後一個非葉結點是第n/2個結點。

以7号結點為根的子樹不符合最小堆的特性，是以要向下調整。

同理以6号、5号和4結點為根的子樹也不符合最小對的特性，都需要往下調整。

下面是已經對7号、6号、5号和4結點為根結點的子樹調整完畢之後的狀态。

當然目前這棵樹仍然不符合最小堆的特性，我們需要繼續調整以3号結點為根的子樹，即将3号結點向下調整。

同理繼續調整以2号結點為根的子樹，最後調整以1号結點為根的子樹。調整完畢之後，整棵樹就符合最小堆的特性啦。

小結一下這個建立堆的算法。把n個元素建立一個堆，首先我可以将這n個結點以自頂向下、從左到右的方式從1到n編碼。這樣就可以把這n個結點轉換成為一棵完全二叉樹。緊接着從最後一個非葉結點（結點編号為n/2）開始到根結點（結點編号為1），逐個掃描所有的結點，根據需要将目前結點向下調整，直到以目前結點為根結點的子樹符合堆的特性。雖然講起來起來很複雜，但是實作起來卻很簡單，隻有兩行代碼如下：

for(i=n/2;i>=1;i--)
    siftdown(i);
           

用這種方法來建立一個堆的時間複雜度是O(N)，如果你感興趣可以嘗試自己證明一下，

堆還有一個作用就是堆排序，與快速排序一樣堆排序的時間複雜度也是O(NlogN)。堆排序的實作很簡單，比如我們現在要進行從小到大排序，可以先建立最小堆，然後每次删除頂部元素并将頂部元素輸出或者放入一個新的數組中，直到堆為空為止。最終輸出的或者存放在新數組中數就已經是排序好的了。

完整代碼如下

package com.usoft.heap;


import java.util.Random;

/**
 * Created by xinxingegeya on 16/6/30.
 */
public class MinHeap<T extends Comparable<T>> {

    /**
     * 最小堆内部使用數組存儲
     */
    private Node<T>[] h;
    private int maximumCapacity; //數組初始化大小
    private int capacity; //堆的大小

    private int index;


    /**
     * 最小堆的大小
     *
     * @param maxCapacity
     */
    public MinHeap(int capacity, int maxCapacity) {
        this.capacity = capacity;
        this.maximumCapacity = maxCapacity;
        h = (Node<T>[]) new Node[maxCapacity];
    }

    /**
     * 使用Node封裝最小堆的元素節點
     *
     * @param <T>
     */
    static class Node<T extends Comparable<T>> implements Comparable<Node> {
        private T data; //節點資料

        public Node(T data) {
            this.data = data;
        }

        public T getData() {
            return data;
        }

        public void setData(T data) {
            this.data = data;
        }

        @Override
        public int compareTo(Node o) {
            return this.data.compareTo((T) o.getData());
        }
    }


    void swap(int x, int y) {
        Node<T> t;
        t = h[x];
        h[x] = h[y];
        h[y] = t;
    }

    //向下調整節點
    void siftDown(int i) {//傳入一個需要向下調整的結點編号i，這裡傳入1，即從堆的頂點開始向下調整
        int t, flag = 0;//flag用來标記是否需要繼續向下調整
        //當i結點有兒子的時候（其實是至少有左兒子的情況下）并且有需要繼續調整的時候循環窒執行
        while (i * 2 <= capacity && flag == 0) {
            //首先判斷他和他左兒子的關系，并用t記錄值較大的結點編号
            if (h[i].compareTo(h[i * 2]) > 0) {
                t = i * 2;
            } else {
                t = i;
            }

            //如果他有右兒子的情況下，再對右兒子進行讨論
            if (i * 2 + 1 <= capacity) {
                //如果右兒子的值更大，更新較小的結點編号
                if (h[t].compareTo(h[i * 2 + 1]) > 0) {
                    t = i * 2 + 1;
                }
            }
            //如果發現最大的結點編号不是自己，說明子結點中有比父結點更大的
            if (t != i) {
                swap(t, i);//交換它們，注意swap函數需要自己來寫
                i = t;//更新i為剛才與它交換的兒子結點的編号，便于接下來繼續向下調整
            } else {
                flag = 1;//則否說明目前的父結點已經比兩個子結點都要大了，不需要在進行調整了
            }
        }
    }

    //向上調整節點
    void siftUp(int i) { //傳入一個需要向上調整的結點編号i
        int flag = 0; //用來标記是否需要繼續向上調整
        if (i == 1) return; //如果是堆頂，就傳回，不需要調整了
        //不在堆頂 并且 目前結點i的值比父結點小的時候繼續向上調整
        while (i != 1 && flag == 0) {
            //判斷是否比父結點的小
            if (h[i].compareTo(h[i / 2]) < 0) {
                swap(i, i / 2);//交換他和他爸爸的位置
            } else {
                flag = 1;//表示已經不需要調整了，目前結點的值比父結點的值要大
            }
            i = i / 2; //這句話很重要，更新編号i為它父結點的編号，進而便于下一次繼續向上調整
        }
    }

    /**
     * 把數組初始化成最小堆
     */
    void creatBySiftDown() {
        int i;
        //從最後一個非葉結點到第1個結點依次進行向上調整
        for (i = capacity / 2; i >= 1; i--) {
            siftDown(i);
        }
    }


    /**
     * 插入元素,并sift up
     *
     * @param data
     */
    void insert(T data) {
        if (capacity < maximumCapacity) {
            Node<T> node = new Node<>(data);
            h[++index] = node;
            siftUp(index);
        } else {
            throw new RuntimeException("heap is full");
        }
    }

    /**
     * 使用最小堆的性質進行堆排序
     *
     * @return
     */
    Node deleteMin() {
        Node node;
        node = h[1];
        h[1] = h[capacity];
        capacity--;
        siftDown(1);
        return node;
    }

    public static void main(String args[]) {

        int maxCapacity = 100;
        int capacity = 9;
        MinHeap<Item> minHeap = new MinHeap<>(capacity, maxCapacity);

        for (int i = 0; i < capacity; i++) {
            Random random = new Random();
            int r = random.nextInt();
            Item item = new Item(Math.abs(r) % 1000);
            minHeap.insert(item);
        }

        for (int i = 1; i <= capacity; i++) {
            System.out.print(minHeap.h[i].getData().getId() + ",");
        }

        System.out.println();

        for (int i = 1; i <= capacity; i++) {
            System.out.println(((Item) minHeap.deleteMin().getData()).getId());
        }
    }
}

           

========END========

版權聲明：本文為CSDN部落客「weixin_34365635」的原創文章，遵循CC 4.0 BY-SA版權協定，轉載請附上原文出處連結及本聲明。

原文連結：https://blog.csdn.net/weixin_34365635/article/details/92644866