http://acm.sdut.edu.cn/sdutoj/problem.php?action=showproblem&problemid=2623
The number of steps
Time Limit: 1000ms Memory limit: 65536K 有疑問?點這裡^_^
題目描述
Mary stands in a strange maze, the maze looks like a triangle(the first layer have one room,the second layer have two rooms,the third layer have three rooms …). Now she stands at the top point(the first layer), and the KEY of this maze is in the lowest layer’s leftmost room. Known that each room can only access to its left room and lower left and lower right rooms .If a room doesn’t have its left room, the probability of going to the lower left room and lower right room are a and b (a + b = 1 ). If a room only has it’s left room, the probability of going to the room is 1. If a room has its lower left, lower right rooms and its left room, the probability of going to each room are c, d, e (c + d + e = 1). Now , Mary wants to know how many steps she needs to reach the KEY. Dear friend, can you tell Mary the expected number of steps required to reach the KEY?
輸入
There are no more than 70 test cases. In each case , first Input a positive integer n(0<n<45), The input is terminated with 0. This test case is not to be processed.
輸出
Please calculate the expected number of steps required to reach the KEY room, there are 2 digits after the decimal point.
示例輸入
3
0.3 0.7
0.1 0.3 0.6
0 示例輸出
3.41 提示
來源
2013年山東省第四屆ACM大學生程式設計競賽
示例程式
分析:
第一行有一個位置,第二行兩個,第三行三個......第n行n個。此時你在最左上角的位置,如果你左面沒有位置,隻能往左下和右下走,機率(a,b)。否則可以往左,左下和右下三個方向走,,機率(c,d,e)。讓你求到達最左下角的期望。
先科普一下數學期望吧:
首先,來看下期望有啥基本的公式。對離散型随機變量x,其機率為p,有
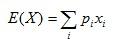
對随機變量A、B,有
第二個式子表明了期望有線性的性質,簡單了解就是期望之間可根據關系,簡單運算(不嚴謹的了解)。 這就為我們解決一個期望問題,不斷轉化為解決另外的期望問題,最終轉化到一個已知的期望上。
舉一個求期望最簡單的例子,見下圖:
假設有個人在 1号節點處,每一分鐘他會緣着邊随機走到一個節點或者在原地停留,問他走到4号節點需要平均幾分鐘?
這是個簡單的期望問題,我們用Ei(i=1,2,3,4) 表示從i号節點走到4号節點的數學期望值。根據題意對1号節點有
E1=(1/3)*E1+(1/3)*E2+(1/3)*E3+1 ①
表示 他下一分鐘可以走到2或者3或在原地1,每個可能機率是1/3 ,注意是下一分鐘,故要加上1.
同理我們對節點2,3同樣可以列出:
E2=(1/3)*E1+(1/3)*E2+(1/3)*E4+1 ②
E3=(1/3)*E1+(1/3)*E3+(1/3)*E4+1 ③
那E4等于多少呢? 很明顯
E4=0 ④
因為他就是要到點4
這樣上面1234式其實就是組成了一組方程組,解方程組就可得出E1!!,用高斯消元,複雜度是O(n^3)
從上述例子,我們可總結出如何解決期望類問題,根據題意,表示出各個狀态的期望(上例的Ei,1234),根據機率公式,列出期望之間的方程,解方程即可。
AC代碼:
1 #include<stdio.h>
2 #include<string.h>
3 double dp[57][57];
4 int main()
5 {
6 int t;
7 while(scanf("%d",&t),t)
8 {
9 int i,j;
10 double a,b,c,d,e;
11 scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e);
12 memset(dp,0,sizeof(dp));
13 dp[t][1]=0;
14 for(i=1;i<=t-1;i++)
15 {
16 dp[t][i+1]+=(dp[t][i]+1);
17 }
18 for(i=t-1;i>=1;i--)
19 {
20 dp[i][1]+=a*(dp[i+1][1]+1)+b*(dp[i+1][2]+1);
21 for(j=2;j<=i;j++)
22 dp[i][j]+=c*(dp[i+1][j]+1)+d*(dp[i+1][j+1]+1)+e*(dp[i][j-1]+1);
23 }
24 printf("%.2lf\n",dp[1][1]);
25 }
26 return 0;
27 } View Code
官方标程:
1 #include <stdio.h>
2 #include <string.h>
3 #include <stdlib.h>
4 #include <string>
5 #include <iostream>
6 #include <map>
7 #include <vector>
8 #include <algorithm>
9 using namespace std;
10 #define MAXN 1000
11 #define eps 1e-8
12 double Atex[MAXN][MAXN];
13 double a[2], b[3];
14 int all;
15 inline int dcmp(double d) {
16 return d < -eps ? -1 : d > eps;
17 }
18
19 void gauss(int n, int m)
20 {
21 int r,c,i,j;
22 for(r=c=0; r<n&&c<m; r++,c++)
23 {
24 for(i=r;i<n;i++)
25 if(dcmp(Atex[i][c])) break;
26 if(i==n)//{r--;continue;}
27 return;
28 if(i!=r) for(j=c;j<=m;j++) swap(Atex[i][j],Atex[r][j]);
29 for(i=r+1;i<n;i++)
30 if(Atex[i][c]!=0)
31 {
32 double temp=Atex[i][c]/Atex[r][c];
33 for(j=c;j<=m;j++)
34 Atex[i][j]-=Atex[r][j]*temp;
35 }
36 }
37 for(i=n-1;i>=0;i--)
38 {
39 Atex[i][m]/=Atex[i][i];
40 Atex[i][i]=1;
41 for(j=i-1;j>=0;j--) Atex[j][m]-=Atex[i][m]*Atex[j][i];
42 }
43 return;
44 }
45
46 void makemap(int n) {
47 memset(Atex, 0, sizeof(Atex));
48 all = (1+n)*n/2;
49 for (int i = 0; i < all; i ++) {
50 Atex[i][i] = 1;
51 Atex[i][all] = 1;
52 }
53 int t = 0, tt;
54 for (int i = 0; i < n-1; i ++) {
55 tt = t + i+1;
56 Atex[t][tt] = -1*a[0];
57 Atex[t][tt+1] = -1*a[1];
58 for (int j = t+1; j < tt; j ++) {
59 Atex[j][j+i+1] = -1*b[0];
60 Atex[j][j+i+2] = -1*b[1];
61 Atex[j][j-1] = -1*b[2];
62 }
63 t = tt;
64 }
65 Atex[t][all] = 0;
66 for (int i = t+1; i < all; i ++) {
67 Atex[i][i-1] = -1;
68 }
69 }
70
71 int main()
72 {
73 int n;
74 while(scanf("%d", &n) != EOF) {
75 if(n == 0) break;
76 for (int i = 0; i < 2; i ++) {
77 scanf("%lf", &a[i]);
78 }
79 for (int i = 0; i < 3; i ++) {
80 scanf("%lf", &b[i]);
81 }
82 makemap(n);
83 gauss(all, all);
84 printf("%.2f\n", Atex[0][all]);
85 }
86 return 0;
87 } View Code
轉載于:https://www.cnblogs.com/jeff-wgc/p/4468199.html