希爾排序(遞減增量排序)
-
- 希爾排序是基于插入排序的以下兩點性質而提出改進方法的:
- 原理
- 算法描述
- 僞代碼
- 代碼
-
- Donald Shell增量
- 其他增量
- 希爾排序是不穩定的排序算法。
- 複雜度
希爾排序是基于插入排序的以下兩點性質而提出改進方法的:
插入排序在對幾乎已經排好序的資料操作時,效率高,即可以達到線性排序的效率
但插入排序一般來說是低效的,因為插入排序每次隻能将資料移動一位
希爾排序通過将比較的全部元素分為幾個區域來提升插入排序的性能
可以讓一個元素可以一次性地朝最終位置前進一大步。
然後算法再取越來越小的步長進行排序,算法的最後一步就是普通的插入排序,但是到了這步,需排序的資料幾乎是已排好的了(此時插入排序較快)。
原理
希爾排序是将待排序的數組元素 按下标的一定增量分組 ,分成多個子序列,然後對各個子序列進行直接插入排序算法排序;
然後依次縮減增量再進行排序,直到增量為1時,進行最後一次直接插入排序,排序結束。
算法描述
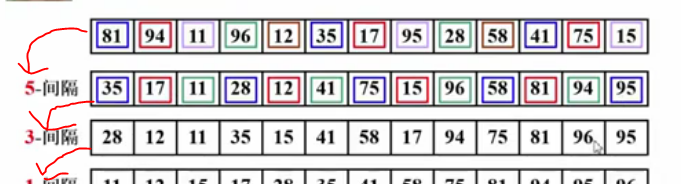
1.先将整個待排序的記錄序列分割成為若幹子序列分别進行直接插入排序,具體算法描述:
2.選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
3.按增量序列個數k,對序列進行 k 趟排序;
4.每趟排序,根據對應的增量ti,将待排序列分割成若幹長度為m 的子序列,分别對各子表進行直接插入排序。
注意:"tk間隔"排序後的有序的序列,在執行"tk+1間隔"排序後,"Dk間隔"排序後的結果依然是有序的
5.僅當增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
僞代碼
代碼
Donald Shell增量
增量元素不互質,則小增量可能根本不起作用
void shellSort(int [] arr){
int temp;
for (int delta = arr.length/2;delta>=1;delta/=2){ //對每個增量進行一次排序
for (int i=delta; i`<arr.length; i++){
for (int j=i;j>=delta && arr[j]<arr[j-delta]; j-=delta){
// 注意每個地方增量和內插補點都是delta
temp=arr[j-delta];
arr[j-delta]=arr[j];
arr[j]=temp;
}
} //loop i
} //loop delta
}
其他增量
void ShellSort( ElementType A[], int N )
{ /* 希爾排序 - 用Sedgewick增量序列 */
int Si, D, P, i;
ElementType Tmp;
/* 這裡隻列出一小部分增量 */
int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};
for ( Si=0; Sedgewick[Si]>=N; Si++ )
; /* 初始的增量Sedgewick[Si]不能超過待排序列長度 */
for ( D=Sedgewick[Si]; D>0; D=Sedgewick[++Si] )
for ( P=D; P<N; P++ ) { /* 插入排序*/
Tmp = A[P];
for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
A[i] = A[i-D];
A[i] = Tmp;
}
}
希爾排序是不穩定的排序算法。
雖然一次插入排序是穩定的,不會改變相同元素的相對順序,但在不同的插入排序過程中,相同的元素可能在各自的插入排序中移動,最後其穩定性就會被打亂。
複雜度
最差時間複雜度 ---- 根據步長序列的不同而不同。已知最好的為O(n(logn)^2)
最優時間複雜度 ---- O(n)