廣度優先搜尋找出的是最短路徑(無權重),而Dijkstra算法找出的是最快路徑(有權重,即權重總和最少的路徑)。此隻适用于有向無環圖。
不能将此算法用于包含負權邊的圖。
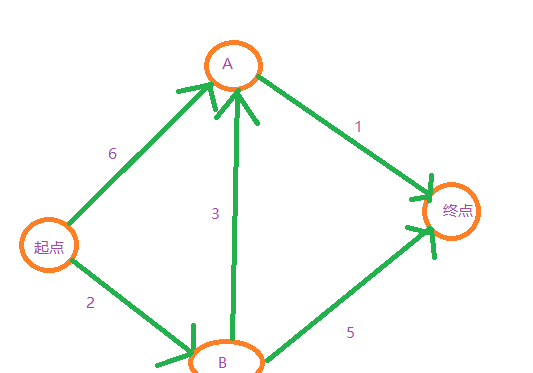
需要三個散清單:
随着算法進行,将不斷更新散清單costs和parents
1 首先建立一個散清單:
2 起點有兩個鄰居A和B,散清單需要同時存儲鄰居和前往鄰居的開銷,如何表示呢:
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
即graph[“start”]是一個散清單(即散清單中包含散清單)
要擷取起點的所有鄰居,可以這樣做:
結果如下:
有一條從起點到A的邊,還有一條從起點到B的邊。如何獲得權重:
print(graph["start"]["a"])
print(graph["start"]["b"])
結果如下:
下面來添加其他節點及其鄰居:
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {}#終點沒有任何鄰居
接下來需要用一個散清單來存儲每個節點的開銷。
節點的開銷指的是從起點出發前往該節點需要多長時間。
從起點到B需要2分鐘,到A需要6分鐘,到終點的時間不知道,設為無窮。
建立開銷表:
infinity = float("inf")#無窮
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity
還需要一個存儲父節點的散清單:
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
最後需要一個數組,用于記錄處理過的點,因為對于同一個節點不用處理多次。
算法流程:
完整代碼:
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {}#終點沒有任何鄰居
infinity = float("inf")#無窮
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
processed = []
def find_lowest_cost_node(costs):
'''
從未被處理的節點中找出最低開銷節點
:param costs: 開銷表
:return: 最低開銷節點
'''
lowest_cost = float("inf")#最低開銷初始設為無窮
lowest_cost_node = None#最低開銷節點初始設為無
for node in costs:#周遊所有節點
cost = costs[node]
if cost < lowest_cost and node not in processed:#如果目前節點開銷更低且未處理過
lowest_cost = cost#就将其視為開銷最低節點
lowest_cost_node = node
return lowest_cost_node
node = find_lowest_cost_node(costs)#從未被處理的節點中找出最低開銷節點
while node is not None:#此循環在所有節點被處理過後結束
cost = costs[node]#此節點的開銷
neighbors = graph[node]#此節點的鄰居,neighbors是一個散清單
for n in neighbors.keys():#周遊鄰居
new_cost = cost + neighbors[n]#開銷指的是 從起點到該節點需要多長時間,而不是從目前節點直接前往鄰居節點
if costs[n] > new_cost:#原來直接前往此鄰居的開銷 和 經過此節點前往該鄰居的開銷對比
costs[n] = new_cost#更新鄰居開銷
parents[n] = node#将該鄰居父節點設為目前節點
processed.append(node)#将該節點标記為處理過
node = find_lowest_cost_node(costs)#找出接下來要處理的節點
print(parents)
print(costs)
最終可以從costs表中看到,fin的開銷為6
從parents表的父節點路徑為fin-a-b-start
練習:
graph = {}
graph["start"] = {}
graph["start"]["a"] = 2
graph["start"]["b"] = 5
graph["a"] = {}
graph["a"]["b"] = 8
graph["a"]["d"] = 7
graph["b"] = {}
graph["b"]["c"] = 4
graph["b"]["d"] = 2
graph["c"] = {}
graph["c"]["fin"] = 3
graph["c"]["d"] = 6
graph["d"] = {}
graph["d"]["fin"] = 1
graph["fin"] = {}#終點沒有任何鄰居
infinity = float("inf")#無窮
costs = {}
costs["a"] = 2
costs["b"] = 5
costs["c"] = infinity
costs["d"] = infinity
costs["fin"] = infinity
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["c"] = None
parents["d"] = None
parents["fin"] = None
processed = []
def find_lowest_cost_node(costs):
'''
從未被處理的節點中找出最低開銷節點
:param costs: 開銷表
:return: 最低開銷節點
'''
lowest_cost = float("inf")#最低開銷初始設為無窮
lowest_cost_node = None#最低開銷節點初始設為無
for node in costs:#周遊所有節點
cost = costs[node]
if cost < lowest_cost and node not in processed:#如果目前節點開銷更低且未處理過
lowest_cost = cost#就将其視為開銷最低節點
lowest_cost_node = node
return lowest_cost_node
node = find_lowest_cost_node(costs)#從未被處理的節點中找出最低開銷節點
while node is not None:#此循環在所有節點被處理過後結束
cost = costs[node]#此節點的開銷
neighbors = graph[node]#此節點的鄰居,neighbors是一個散清單
for n in neighbors.keys():#周遊鄰居
new_cost = cost + neighbors[n]#開銷指的是 從起點到該節點需要多長時間,而不是從目前節點直接前往鄰居節點
if costs[n] > new_cost:#原來直接前往此鄰居的開銷 和 經過此節點前往該鄰居的開銷對比
costs[n] = new_cost#更新鄰居開銷
parents[n] = node#将該鄰居父節點設為目前節點
processed.append(node)#将該節點标記為處理過
node = find_lowest_cost_node(costs)#找出接下來要處理的節點
print(parents)
print(costs)
最終可以從costs表中看到,fin的開銷為8
從parents表看出父節點路徑為fin-d-b-start