Boosting ---- 加法模型、前向分步、Gradient Boosting、AdaBoost、GBDT

加法模型

加法模型 (additive model) 形式如下：

f ( x ) = ∑ m = 1 M β m b ( x ; γ m ) f(x) = \sum_{m=1}^{M}\beta_mb(x;\gamma_m) f(x)=m=1∑Mβmb(x;γm)

其中， b ( x ; γ m ) b(x;\gamma_m) b(x;γm)是第 m m m個基函數， γ m \gamma_m γm是第 m m m個基函數的模型參數， β m \beta_m βm是第 m m m個基函數的權重。由此可見，加法模型實際上由一系列基函數的權重相加得到。

在給定訓練資料 { ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x N , y N ) } \{(x_0, y_0), (x_1, y_1), ..., (x_N, y_N)\} {(x0,y0),(x1,y1),...,(xN,yN)}及損失函數 L ( y , f ( x ) ) L(y, f(x)) L(y,f(x))的情況下，學習加法模型 f ( x ) f(x) f(x)即損失函數極小化問題：

min ⁡ β m , γ m ∑ i = 1 N L ( y i , ∑ m = 1 M β m b ( x i ; γ m ) ) \min_{\beta_m, \gamma_m}\sum_{i=1}^{N}L(y_i, \sum_{m=1}^{M}\beta_mb(x_i;\gamma_m)) βm,γmmini=1∑NL(yi,m=1∑Mβmb(xi;γm))

是以可以看出加法模型的學習過程實際上是一個非常複雜的優化問題。

前向分步算法

前向分步算法 (forward stagewise algorithm) 是求解上述優化問題的一種算法，其思想是：從前往後，每一步隻學習一個基函數及其系數，逐漸逼近優化損失函數，進而簡化優化的複雜度。其算法過程如下：

輸入：訓練資料集 { ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x N , y N ) } \{(x_0, y_0), (x_1, y_1), ..., (x_N, y_N)\} {(x0,y0),(x1,y1),...,(xN,yN)}；損失函數 L ( y , f ( x ) ) L(y, f(x)) L(y,f(x))；基函數集 { b ( x ; γ ) } \{b(x;\gamma)\} {b(x;γ)} (參數未優化)

輸出：加法模型 f ( x ) f(x) f(x)

初始化 f 0 ( x ) = 0 f_0(x) = 0 f0(x)=0
對 m = 1 , 2 , . . . , M m=1, 2, ..., M m=1,2,...,M

(1) 極小化損失函數，得到參數 β m , γ m \beta_m, \gamma_m βm,γm

( β m , γ m ) = arg ⁡ min ⁡ β , γ ∑ i = 1 N L ( y i , f m − 1 ( x i ) + β b ( x i ; γ ) ) (\beta_m, \gamma_m) = \arg\min_{\beta, \gamma} \sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+\beta b(x_i;\gamma)) (βm,γm)=argβ,γmini=1∑NL(yi,fm−1(xi)+βb(xi;γ))

(2) 更新

f m ( x ) = f m − 1 ( x ) + β m b ( x ; γ m ) f_m(x) = f_{m-1}(x)+\beta_m b(x;\gamma_m) fm(x)=fm−1(x)+βmb(x;γm)
得到最終的加法模型

f ( x ) = f m ( x ) = ∑ m = 1 M β m b ( x ; γ m ) f(x) = f_m(x) = \sum_{m=1}^{M}\beta_mb(x;\gamma_m) f(x)=fm(x)=m=1∑Mβmb(x;γm)

前向分步算法将同時求解 M M M個基函數的參數及系數的優化問題，簡化成了逐漸求解每個基函數的參數及系數的優化問題。前向分步算法的第 m m m個基函數參數及系數 β m , γ m \beta_m, \gamma_m βm,γm的确定，僅考慮目前狀态下使損失函數極小化即局部最優解，是一種貪婪算法，不一定能夠得到全局最優解。

內建模型的提升 (Boosting) 方法即采用了加法模型與前向分布算法。以決策樹為基函數的提升方法成為提升樹。

AdaBoost

Adaboost是一種疊代算法，其核心思想是針對同一個訓練集訓練不同的分類器 (弱分類器)，然後把這些弱分類器集合起來，構成一個更強的最終分類器 (強分類器)。AdaBoost是一種內建學習中的Boosting算法。

AdaBoost的主要思想：

先訓練出一個基學習器
根據該學習器的表現對訓練樣本分布進行調整，使得現有基學習器做錯的樣本在後續學習器的訓練中受到更多關注 (即增權重重)
基于調整後的樣本分布來訓練下一個基學習器
如此重複進行直至基學習器數目達到事先指定的值 M M M
最終将這 M M M個基學習器進行權重結合

AdaBoost的函數形式如下：

H ( x ) = ∑ m = 1 M α m h m ( x ) H(x) = \sum_{m=1}^{M}\alpha_m h_m(x) H(x)=m=1∑Mαmhm(x)

由此可見，AdaBoost是一種加法模型。AdaBoost的損失函數采用指數損失：

L o s s = ∑ i = 1 N e − y i H ( x i ) Loss = \sum_{i=1}^{N}e^{-y_iH(x_i)} Loss=i=1∑Ne−yiH(xi)

在這裡， y i ∈ { − 1 , + 1 } y_i \in \{-1, +1\} yi∈{−1,+1}。

當 y i = H ( x i ) y_i = H(x_i) yi=H(xi)時， − y i H ( x i ) = − 1 -y_iH(x_i) = -1 −yiH(xi)=−1

當 y i ≠ H ( x i ) y_i \not= H(x_i) yi=H(xi)時， − y i H ( x i ) = 1 -y_iH(x_i) = 1 −yiH(xi)=1

AdaBoost算法過程如下：

輸入：訓練資料集 { ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x N , y N ) } \{(x_0, y_0), (x_1, y_1), ..., (x_N, y_N)\} {(x0,y0),(x1,y1),...,(xN,yN)}，其中 y i ∈ { − 1 , + 1 } y_i \in \{-1, +1\} yi∈{−1,+1}；基分類器 { h ( x ) } \{h(x)\} {h(x)} (參數未優化)

輸出：強分類器 H ( x ) H(x) H(x)

初始化訓練資料的權值分布 D 1 = ( w 1 , 1 , w 1 , 2 , … , w 1 , N ) , w 1 , i = 1 N , i = 1 , 2 , … , N D_1=(w_{1,1},w_{1,2},…,w_{1,N}),w_{1,i}=\frac{1}{N},i=1,2,…,N D1=(w1,1,w1,2,…,w1,N),w1,i=N1,i=1,2,…,N
對 m = 1 , 2 , . . . , M m=1, 2, ..., M m=1,2,...,M

(1) 使用具有權值分布 D m D_m Dm的訓練集進行學習，得到弱分類器 h m ( x ) h_m(x) hm(x)

(2) 計算 h m ( x ) h_m(x) hm(x)在目前資料集上的分類誤差：

e m = ∑ i = 1 N w m , i I ( h m ( x i ) ≠ y i ) e_m=\sum_{i=1}^Nw_{m,i} I(h_m (x_i )≠y_i ) em=i=1∑Nwm,iI(hm(xi)=yi)

(3) 計算 h m ( x ) h_m(x) hm(x)在強分類器中所占的權重：

α m = 1 2 l o g 1 − e m e m α_m=\frac{1}{2}log \frac{1-e_m}{e_m} αm=21logem1−em

(4) 更新訓練資料集的權值分布， z m z_m zm是歸一化因子，為了使樣本的機率分布和為1：

w m + 1 , i = w m , i e − α m y i h m ( x i ) z m ， i = 1 , 2 , … , N w_{m+1,i}=\frac{w_{m,i}e^{-α_m y_i h_m (x_i )}}{z_m}，i=1,2,…,N wm+1,i=zmwm,ie−αmyihm(xi)，i=1,2,…,N

z m = ∑ i = 1 N w m , i e − α m y i h m ( x i ) z_m=\sum_{i=1}^Nw_{m,i}e^{-α_m y_i h_m (x_i )} zm=i=1∑Nwm,ie−αmyihm(xi)
得到最終的強分類器

H ( x ) = ∑ m = 1 M α m h m ( x ) H(x) = \sum_{m=1}^{M}\alpha_mh_m(x) H(x)=m=1∑Mαmhm(x)

其中， I ( h m ( x i ) ≠ y i ) ∈ { 0 , 1 } I(h_m (x_i )≠y_i ) \in \{0, 1\} I(hm(xi)=yi)∈{0,1}，當其值為真時函數值為1，其值為假時函數值為0。

從前向分步算法到AdaBoost

AdaBoost算法實際上是前向分步算法的一種特例。

當加法模型的基函數是弱分類器，損失函數是指數函數時，使用前向分步算法學習到的加法模型等價于AdaBoost算法的最終分類器：

f ( x ) = ∑ m = 1 M α m h m ( x ) f(x) = \sum_{m=1}^{M}\alpha_mh_m(x) f(x)=m=1∑Mαmhm(x)

假設經過 m − 1 m-1 m−1輪疊代後前向分布算法得到了 f m − 1 ( x ) f_{m-1}(x) fm−1(x)：

f m − 1 ( x ) = ∑ i = 1 m − 1 α i h i ( x ) f_{m-1}(x) = \sum_{i=1}^{m-1}\alpha_ih_i(x) fm−1(x)=i=1∑m−1αihi(x)

那麼，在第 m m m輪疊代時，根據前向分布算法，需要得到 α m \alpha_m αm和 h m ( x ) h_m(x) hm(x)，使 f m ( x ) f_m(x) fm(x)在訓練集上的損失最小。

( α m , h m ( x ) ) = arg ⁡ min ⁡ α , h ∑ i = 1 N L ( y i , f m − 1 ( x i ) + α h ( x i ) ) = arg ⁡ min ⁡ α , h ∑ i = 1 N e − y i ( f m − 1 ( x i ) + α h ( x i ) = arg ⁡ min ⁡ α , h ∑ i = 1 N e − y i f m − 1 ( x i ) e − y i α h ( x i ) = arg ⁡ min ⁡ α , h ∑ i = 1 N w m i e − y i α h ( x i ) (\alpha_m, h_m(x)) = \arg\min_{\alpha, h} \sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+\alpha h(x_i)) \\ = \arg\min_{\alpha, h} \sum_{i=1}^{N}e^{-y_i(f_{m-1}(x_i)+\alpha h(x_i)} \\ = \arg\min_{\alpha, h} \sum_{i=1}^{N}e^{-y_if_{m-1}(x_i)}e^{-y_i\alpha h(x_i)} \\ = \arg\min_{\alpha, h} \sum_{i=1}^{N}w_{mi}e^{-y_i\alpha h(x_i)} (αm,hm(x))=argα,hmini=1∑NL(yi,fm−1(xi)+αh(xi))=argα,hmini=1∑Ne−yi(fm−1(xi)+αh(xi)=argα,hmini=1∑Ne−yifm−1(xi)e−yiαh(xi)=argα,hmini=1∑Nwmie−yiαh(xi)

其中， w m i = e − y i f m − 1 ( x i ) w_{mi} = e^{-y_if_{m-1}(x_i)} wmi=e−yifm−1(xi)， w m i w_{mi} wmi不依賴于 α , h \alpha, h α,h，是以與最小化無關，但是 w m i w_{mi} wmi依賴于 f m ( x ) f_m(x) fm(x)，随着每一輪的疊代變化。

對任意的 α > 0 \alpha > 0 α>0，使上式最小的 h m ( x ) h_m(x) hm(x)可由下式得到：

h m ( x ) = arg ⁡ min ⁡ h ∑ i = 1 N w m i e − y i h ( x i ) ) h_m(x) = \arg\min_{h} \sum_{i=1}^{N}w_{mi}e^{-y_ih(x_i))} hm(x)=arghmini=1∑Nwmie−yih(xi))

在不考慮規範因子 z z z的情況下，上式的 h m ( x ) h_m(x) hm(x)即表示第 m m m輪在權重分布為 w m w_m wm的訓練資料下使指數損失函數最小的弱分類器，即為AdaBoost中第 m m m輪的基本分類器 h m ( x ) h_m(x) hm(x)。

然後，在最優化 arg ⁡ min ⁡ α , h ∑ i = 1 N w m i e − y i α h ( x i ) ) \arg\min_{\alpha, h} \sum_{i=1}^{N}w_{mi}e^{-y_i\alpha h(x_i))} argminα,h∑i=1Nwmie−yiαh(xi))式中，

∑ i = 1 N w m i e − y i α h ( x i ) ) = ∑ y i ≠ h m ( x i ) w m i e α + ∑ y i = h m ( x i ) w m i e − α = e α ∑ i = 1 N w m i I ( h m ( x i ) ≠ y i ) + e − α ∑ i = 1 N w m i ( 1 − I ( h m ( x i ) ≠ y i ) ) = ( e α − e − α ) ∑ i = 1 N w m i I ( h m ( x i ) ≠ y i ) + e − α ∑ i = 1 N w m i \sum_{i=1}^{N}w_{mi}e^{-y_i\alpha h(x_i))} = \sum_{y_i\not = h_m(x_i)}w_{mi}e^{\alpha} + \sum_{y_i = h_m(x_i)}w_{mi}e^{-\alpha} \\ = e^{\alpha}\sum_{i=1}^{N}w_{mi}I(h_m (x_i )≠y_i ) + e^{-\alpha}\sum_{i=1}^{N}w_{mi}(1 - I(h_m (x_i )≠y_i )) \\ = (e^{\alpha} - e^{-\alpha})\sum_{i=1}^{N}w_{mi}I(h_m (x_i )≠y_i ) + e^{-\alpha}\sum_{i=1}^{N}w_{mi} i=1∑Nwmie−yiαh(xi))=yi=hm(xi)∑wmieα+yi=hm(xi)∑wmie−α=eαi=1∑NwmiI(hm(xi)=yi)+e−αi=1∑Nwmi(1−I(hm(xi)=yi))=(eα−e−α)i=1∑NwmiI(hm(xi)=yi)+e−αi=1∑Nwmi

對上式求 α \alpha α的導數并為0，得到 α m \alpha_m αm：

α m = 1 2 log ⁡ 1 − e m e m \alpha_m = \frac{1}{2}\log\frac{1-e_m}{e_m} αm=21logem1−em

其中， e m e_m em是權重分布為 w m w_m wm的訓練資料在弱分類器 h m ( x ) h_m(x) hm(x)下的分類誤差率：

e m = ∑ i = 1 N w m i I ( h m ( x i ) ≠ y i ) ∑ i = 1 N w m i e_m = \frac{\sum_{i=1}^{N}w_{mi}I(h_m (x_i )≠y_i )}{\sum_{i=1}^{N}w_{mi}} em=∑i=1Nwmi∑i=1NwmiI(hm(xi)=yi)

是以，這裡的 α m \alpha_m αm與AdaBoost算法得出的 α m \alpha_m αm完全一緻。

最後，第 m + 1 m+1 m+1輪權重的更新如下:

w m + 1 , i = e − y i f m ( x i ) = e − y i f m − 1 ( x i ) e − y i α h m ( x i ) = w m i e − y i α h m ( x i ) w_{m+1, i} = e^{-y_if_{m}(x_i)} = e^{-y_if_{m-1}(x_i)}e^{-y_i\alpha h_{m}(x_i)} = w_{mi}e^{-y_i\alpha h_{m}(x_i)} wm+1,i=e−yifm(xi)=e−yifm−1(xi)e−yiαhm(xi)=wmie−yiαhm(xi)

這與AdaBoost算法中樣本權重的更新隻相差規範化因子，是以等價。

Gradient Boost

當損失函數是指數函數時，對于前向分步算法中2.1的最優化過程是比較直覺簡單的。但是，對一般的損失函數而言，優化并不是一個容易的過程。Freidman提出了梯度提升 (Gradient Boost)算法，這是使用最速下降 (Steepest Descend)對更一般的損失函數進行優化。

一種常見的思想是不斷疊代更新目前自變量空間的狀态，逼近函數空間上的極小值，來對最優化過程求解。梯度下降就是這樣的一種算法。某點的梯度是函數在該點上升最快的方向，是以梯度的反方向是函數下降再快的地方。梯度下降算法的表達式如下：

x k + 1 = x k − α ⋅ ∇ f ( x k ) \bm x_{k+1} = \bm x_{k} - \alpha \cdot \nabla f(\bm x_{k}) xk+1=xk−α⋅∇f(xk)

其中， α \alpha α是步長，也叫做學習率，控制每次更新的大小。

最速下降法（Steepest descent）是梯度下降法的一種更具體實作形式，其理念為在每次疊代中選擇合适的步長 α k \alpha_k αk，使得目标函數值能夠得到最大程度的減少。

對于每一次疊代，沿梯度的反方向，總可以找到一個 α k \alpha_k αk， x k + 1 = x k − α k ⋅ ∇ f ( x k ) \bm x_{k+1} = \bm x_{k} - \alpha_k \cdot \nabla f(\bm x_{k}) xk+1=xk−αk⋅∇f(xk)在這個方向上更新後函數 f ( x k + 1 ) f(x_{k+1}) f(xk+1)取最小值。

α k = arg ⁡ min ⁡ α ≥ 0 f ( x k − α ∇ f ( x k ) ) \alpha_k = \mathop{\arg\min}_{\alpha \ge 0} f(\bm x_{k} - \alpha \nabla f(\bm x_{k})) αk=argminα≥0f(xk−α∇f(xk))

相比之下，最速下降每一步的步長是搜尋得到的，而梯度下降的步長是預先設定的。

（實際上，在下降的過程中，點的位置在發生改變，對應的梯度也在發生變化，而下降的方向并沒有改變，都是初始點的梯度反方向，這就意味着沿初始點的梯度方向并不一定是下降最快的過程。上式隻是最速下降使用歐式範數的特殊情況，不使用歐式範數時最速下降和梯度下降的方向不一定一樣，具體可以查找相關資料。）

那麼，對于前向分步算法中2.1的最優化過程，使用最速梯度下降算法進行求解。那麼，每次函數更新的過程如下:

f m ( x ) = f m − 1 ( x ) − ρ m [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) f_m(x) = f_{m-1}(x) - \rho_m {[\frac{\partial{L(y_i, f(x_i)) }}{\partial{f(x_i ) } } ] _{f(x) = f_{m-1}(x)}} fm(x)=fm−1(x)−ρm[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)

ρ m \rho_m ρm是函數最速下降的步長。考慮到加法函數的形式：

f m ( x ) = ∑ i = 1 m − 1 β i b ( x ; γ i ) + β m b ( x ; γ m ) = f m − 1 ( x ) + β m b ( x ; γ m ) f_m(x) = \sum_{i=1}^{m-1}\beta_ib(x;\gamma_i) + \beta_mb(x;\gamma_m) = f_{m-1}(x)+ \beta_mb(x;\gamma_m) fm(x)=i=1∑m−1βib(x;γi)+βmb(x;γm)=fm−1(x)+βmb(x;γm)

是以可見， b ( x ; γ m ) b(x;\gamma_m) b(x;γm)作為第 m m m個基函數，需要對梯度的反方向進行拟合，而它的權重應該是最速下降的步長。

那麼最優的 b ( x ; γ m ) b(x;\gamma_m) b(x;γm)應該由下式确定：

y ~ i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) \tilde y_i= - {[\frac{\partial{L(y_i, f(x_i)) }}{\partial{f(x_i ) } } ] _{f(x) = f_{m-1}(x)}} y~i=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)

γ m = arg ⁡ min ⁡ 1 2 ∑ i = 1 N [ y ~ i − b ( x i ; γ m ) ] 2 \gamma_m = \mathop{\arg\min}\frac{1}{2}\sum_{i=1}^{N}[\tilde y_i - b(x_i;\gamma_m)]^2 γm=argmin21i=1∑N[y~i−b(xi;γm)]2

而權重即步長 ρ m \rho_m ρm由最速下降的定義确定：

ρ m = arg ⁡ min ⁡ ρ ≥ 0 f ( x k − ρ ∇ f ( x k ) ) = arg ⁡ min ⁡ ρ ≥ 0 ∑ i = 1 N L ( y i , f m − 1 ( x ) + ρ b ( x ; γ m ) ) \rho_m = \mathop{\arg\min}_{\rho \ge 0} f(\bm x_{k} - \rho\nabla f(\bm x_{k})) \\ = \mathop{\arg\min}_{\rho \ge 0}\sum_{i=1}^{N}L(y_i, f_{m-1}(x) + \rho b(x;\gamma_m)) ρm=argminρ≥0f(xk−ρ∇f(xk))=argminρ≥0i=1∑NL(yi,fm−1(x)+ρb(x;γm))

最後，更新加法模型：

f m ( x ) = f m − 1 ( x ) + ρ b ( x ; γ m ) f_m(x) = f_{m-1}(x) + \rho b(x;\gamma_m) fm(x)=fm−1(x)+ρb(x;γm)

以上就是Gradient Boosting的過程，GB實際上是使用最速下降對前向分步算法的優化過程求解的一種算法。Gradient Boosting的通用解法如下：

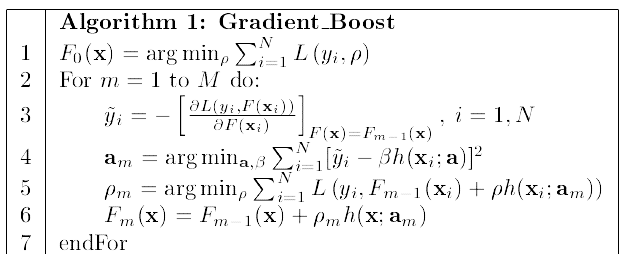
Boosting ---- 加法模型、前向分步、Gradient Boosting、AdaBoost、GBDT

GBDT回歸樹

考慮損失函數為平方誤差函數的情況：

L o s s = 1 2 ∑ i N ( y i − f ( x ) ) 2 Loss = \frac{1}{2}\sum_{i}^{N}(y_i-f(x))^2 Loss=21i∑N(yi−f(x))2

此時，根據Gradient Boosting算法在第 m m m步時的梯度反方向如下：

y ~ i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) = y i − f ( x i ) \tilde y_i= - {[\frac{\partial{L(y_i, f(x_i)) }}{\partial{f(x_i ) } } ] _{f(x) = f_{m-1}(x)}} = y_i - f(x_i) y~i=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)=yi−f(xi)

即為殘差，由此可見，在損失函數為平方誤差函數時，基函數拟合梯度的反方向實際上可看作基函數拟合殘差。

第 m m m步時， b ( x ; γ m ) b(x;\gamma_m) b(x;γm)由下式确定：

γ m = arg ⁡ min ⁡ ∑ i = 1 N 1 2 [ y ~ i − β b ( x i ; γ m ) ] 2 \gamma_m = \mathop{\arg\min}\sum_{i=1}^{N}\frac{1}{2}[\tilde y_i - \beta b(x_i;\gamma_m)]^2 γm=argmini=1∑N21[y~i−βb(xi;γm)]2

而對于步長 ρ m \rho_m ρm：

ρ m = arg ⁡ min ⁡ ρ ≥ 0 f ( x k − ρ ∇ f ( x k ) ) = arg ⁡ min ⁡ ∑ i = 1 N L ( y i , f m − 1 ( x ) + ρ b ( x ; γ m ) ) = arg ⁡ min ⁡ ∑ i = 1 N 1 2 ( y i − f m − 1 ( x i ) − ρ b ( x i ; γ m ) ) 2 = arg ⁡ min ⁡ ∑ i = 1 N 1 2 ( y ~ i − ρ b ( x i ; γ m ) ) 2 \rho_m = \mathop{\arg\min}_{\rho \ge 0} f(\bm x_{k} - \rho\nabla f(\bm x_{k})) \\ = \mathop{\arg\min}\sum_{i=1}^{N}L(y_i, f_{m-1}(x) + \rho b(x;\gamma_m)) \\ =\arg\min \sum_{i=1}^{N}\frac{1}{2}(y_i - f_{m-1}(x_i) - \rho b(x_i;\gamma_m))^2 \\ = \arg\min \sum_{i=1}^{N}\frac{1}{2}(\tilde y_i - \rho b(x_i;\gamma_m))^2 ρm=argminρ≥0f(xk−ρ∇f(xk))=argmini=1∑NL(yi,fm−1(x)+ρb(x;γm))=argmini=1∑N21(yi−fm−1(xi)−ρb(xi;γm))2=argmini=1∑N21(y~i−ρb(xi;γm))2

從以上兩式可以看出，實際上 γ m \gamma_m γm 的優化過程和 ρ m \rho_m ρm的優化過程是等價的， ρ m \rho_m ρm的求解等價于求解 γ m \gamma_m γm的 β m \beta_m βm。是以，可以使用同一個優化過程：

( β m , γ m ) = arg ⁡ min ⁡ β , γ ∑ i = 1 N 1 2 ( y ~ i − β b ( x i ; γ ) ) 2 ρ m = β m (\beta_m, \gamma_m) = \arg\min_{\beta, \gamma} \sum_{i=1}^{N}\frac{1}{2}(\tilde y_i - \beta b(x_i;\gamma))^2 \\ \rho_m = \beta_m (βm,γm)=argβ,γmini=1∑N21(y~i−βb(xi;γ))2ρm=βm

如果我們令基函數為一個回歸樹模型，第 m m m步時的樹模型 T ( x ) = β b ( x ; γ ) T(x) = \beta b(x;\gamma) T(x)=βb(x;γ)，那麼根據上式可知，

T m ( x ) = arg ⁡ min ⁡ T ∑ i = 1 N 1 2 ( y ~ i − T ( x i ) ) 2 T_m(x) = \arg\min_{T} \sum_{i=1}^{N}\frac{1}{2}(\tilde y_i - T(x_i))^2 Tm(x)=argTmini=1∑N21(y~i−T(xi))2

是以，可見，第 m m m步的最優樹模型 T m ( x ) T_m(x) Tm(x)實際上是對上一步模型的殘差在最小平方誤差下的拟合。

最終得到的回歸提升樹模型如下：

f ( x ) = ∑ m = 1 M T m ( x ) f(x) =\sum_{m=1}^{M}T_m(x) f(x)=m=1∑MTm(x)

上述過程正是GBDT (Gradient Boosting Decision Tree) 用于回歸的訓練過程。實際上在GBDT的實作過程中，為了正則化防止過拟合，在每一步更新模型時往往會進行shrink，即對新的樹模型乘以一個較小的權重：

f m ( x ) = f m − 1 ( x ) + v T m ( x ) f_m(x) = f_{m-1}(x) + v T_m(x) fm(x)=fm−1(x)+vTm(x)

其中， v v v也叫做學習率，是人工設定的超參數。

由上述可見，GBDT中的每一輪的子樹拟合的是上一輪模型的殘差，是以模型的殘差等于該模型此時的梯度的反方向。當加法模型的損失函數是平方誤差函數時，此時殘差和梯度反方向才等價，是以說，拟合的不是殘差，而是梯度。而GBDT隻是Gradient Boosting殘差等價于梯度的一種特殊情況。

上述過程是GBDT用于回歸的一種情況，實際上GBDT也可以用作分類，相對于回歸過程多進行了一步Logistic變換，此文不再進行闡述。

GBDT源碼分析

這裡僅分析 sklearn.ensemble.GradientBoostingRegressor：

class GradientBoostingRegressor(BaseGradientBoosting, RegressorMixin):
    _SUPPORTED_LOSS = ('ls', 'lad', 'huber', 'quantile')
    def __init__(self, loss='ls', learning_rate=0.1, n_estimators=100,
                 subsample=1.0, criterion='friedman_mse', min_samples_split=2,
                 min_samples_leaf=1, min_weight_fraction_leaf=0.,
                 max_depth=3, min_impurity_decrease=0.,
                 min_impurity_split=None, init=None, random_state=None,
                 max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None,
                 warm_start=False, presort='auto', validation_fraction=0.1,
                 n_iter_no_change=None, tol=1e-4):
        super().__init__(
            loss=loss, learning_rate=learning_rate, n_estimators=n_estimators,
            criterion=criterion, min_samples_split=min_samples_split,
            min_samples_leaf=min_samples_leaf,
            min_weight_fraction_leaf=min_weight_fraction_leaf,
            max_depth=max_depth, init=init, subsample=subsample,
            max_features=max_features,
            min_impurity_decrease=min_impurity_decrease,
            min_impurity_split=min_impurity_split,
            random_state=random_state, alpha=alpha, verbose=verbose,
            max_leaf_nodes=max_leaf_nodes, warm_start=warm_start,
            presort=presort, validation_fraction=validation_fraction,
            n_iter_no_change=n_iter_no_change, tol=tol)
    def predict(self, X):
        X = check_array(X, dtype=DTYPE, order="C", accept_sparse='csr')
        # In regression we can directly return the raw value from the trees.
        return self._raw_predict(X).ravel()
    def staged_predict(self, X):
        for raw_predictions in self._staged_raw_predict(X):
            yield raw_predictions.ravel()
    def apply(self, X):
        leaves = super().apply(X)
        leaves = leaves.reshape(X.shape[0], self.estimators_.shape[0])
        return leaves

這裡可以看出，GradientBoostingRegressor類繼承的是BaseGradientBoosting，其損失函數取值有4種。分析BaseGradientBoosting中的_fit_stage函數。

在該函數中，可以看到模型循環K次，每次計算殘差residual，然後建構一個新的樹模型（sklearn中的模型均為改進後的CART樹）對殘差拟合，然後儲存該樹，并根據學習率對Loss進行更新。

class BaseGradientBoosting(BaseEnsemble, metaclass=ABCMeta):
	def _fit_stage(self, i, X, y, raw_predictions, sample_weight, sample_mask,
                   random_state, X_idx_sorted, X_csc=None, X_csr=None):
        assert sample_mask.dtype == np.bool
        loss = self.loss_
        original_y = y
        raw_predictions_copy = raw_predictions.copy()
        for k in range(loss.K):
            if loss.is_multi_class:
                y = np.array(original_y == k, dtype=np.float64)
            # 計算殘差
            residual = loss.negative_gradient(y, raw_predictions_copy, k=k,
                                              sample_weight=sample_weight)

            # induce regression tree on residuals
            tree = DecisionTreeRegressor(
                criterion=self.criterion,
                splitter='best',
                max_depth=self.max_depth,
                min_samples_split=self.min_samples_split,
                min_samples_leaf=self.min_samples_leaf,
                min_weight_fraction_leaf=self.min_weight_fraction_leaf,
                min_impurity_decrease=self.min_impurity_decrease,
                min_impurity_split=self.min_impurity_split,
                max_features=self.max_features,
                max_leaf_nodes=self.max_leaf_nodes,
                random_state=random_state,
                presort=self.presort)

            if self.subsample < 1.0:
                # no inplace multiplication!
                sample_weight = sample_weight * sample_mask.astype(np.float64)

            X = X_csr if X_csr is not None else X
            tree.fit(X, residual, sample_weight=sample_weight,
                     check_input=False, X_idx_sorted=X_idx_sorted)
            # update tree leaves
            loss.update_terminal_regions(
                tree.tree_, X, y, residual, raw_predictions, sample_weight,
                sample_mask, learning_rate=self.learning_rate, k=k)
            # add tree to ensemble
            self.estimators_[i, k] = tree

        return raw_predictions

在這裡，模型每次使用loss.negative_gradient計算殘差residual。考慮loss類中的negative_gradient函數，在scikit-learn/sklearn/ensemble/_gb_losses.py中：

class LeastSquaresError(RegressionLossFunction):
    def negative_gradient(self, y, raw_predictions, **kargs):
        return y - raw_predictions.ravel()

class LeastAbsoluteError(RegressionLossFunction):
    def negative_gradient(self, y, raw_predictions, **kargs):
        raw_predictions = raw_predictions.ravel()
        return 2 * (y - raw_predictions > 0) - 1

class HuberLossFunction(RegressionLossFunction):
    def negative_gradient(self, y, raw_predictions, sample_weight=None,
                          **kargs):
        raw_predictions = raw_predictions.ravel()
        diff = y - raw_predictions
        if sample_weight is None:
            gamma = np.percentile(np.abs(diff), self.alpha * 100)
        else:
            gamma = _weighted_percentile(np.abs(diff), sample_weight,
                                         self.alpha * 100)
        gamma_mask = np.abs(diff) <= gamma
        residual = np.zeros((y.shape[0],), dtype=np.float64)
        residual[gamma_mask] = diff[gamma_mask]
        residual[~gamma_mask] = gamma * np.sign(diff[~gamma_mask])
        self.gamma = gamma
        return residual

class QuantileLossFunction(RegressionLossFunction):
    def negative_gradient(self, y, raw_predictions, **kargs):
        alpha = self.alpha
        raw_predictions = raw_predictions.ravel()
        mask = y > raw_predictions
        return (alpha * mask) - ((1 - alpha) * ~mask)

可以看出上述過程的傳回值以residual命名，實際上求的都是各個Loss函數對應的梯度。

其它

求解最優化過程中，僅使用了梯度，即一階導數，考慮再使用二階導數，是否能夠優化求解過程？（xgboost）
分類樹與回歸樹的過程？
GBDT中兩個優化過程與同時優化如何證明等價？
不使用最速下降，直接使用梯度下降？

參考資料

Friedman論文：Greedy function approximation: a gradient boosting machine.
李航《統計學習方法》P144 - P150
GBDT算法梳理: https://zhuanlan.zhihu.com/p/58105824

Boosting ---- 加法模型、前向分步、Gradient Boosting、AdaBoost、GBDT

加法模型

前向分步算法

AdaBoost

從前向分步算法到AdaBoost

Gradient Boost

GBDT回歸樹

GBDT源碼分析

其它

參考資料

繼續閱讀

機器學習實戰（6）--AdaBoost

金融評分卡項目—4.GBDT模型在流失預警模型中的應用

機器學習筆記04梯度提升樹(GBDT)調參

深入了解提升樹（Boosting tree）算法1. Boosting基本概念2. 前向分步加法模型3. 提升樹4. 回歸提升樹示例5. 完整的示例代碼6. 關于提升樹的若幹問題思考7. 總結8. Reference

GBDT(梯度提升決策樹)算法梳理

機器學習方法篇(9)------梯度提升決策樹GBDT導語GBDT結語

從決策樹到gbdt

GBDT和XGboost介紹

随機森林，GBDT，XGBoost的對比随機森林，GBDT，XGBoost的對比

[機器學習 ] RandomForest、GBDT、XGBoost、lightGBM 原理與差別

GBDT、XGBoost、LightGBM的差別和聯系

詳解最大似然估計（MLE）、最大後驗機率估計（MAP），以及貝葉斯公式的了解

BP神經網絡的Python實作

深度學習推薦系統-筆記08：傳統推薦算法發展彙總

AdaBoost數學原理

Adaboost的原理、推導與執行個體