題目描述
CC C國有n n n個大城市和m mm 條道路,每條道路連接配接這 nnn個城市中的某兩個城市。任意兩個城市之間最多隻有一條道路直接相連。這 mmm 條道路中有一部分為單向通行的道路,一部分為雙向通行的道路,雙向通行的道路在統計條數時也計為 11 1條。
CC C國幅員遼闊,各地的資源分布情況各不相同,這就導緻了同一種商品在不同城市的價格不一定相同。但是,同一種商品在同一個城市的買入價和賣出價始終是相同的。
商人阿龍來到 CCC 國旅遊。當他得知同一種商品在不同城市的價格可能會不同這一資訊之後,便決定在旅遊的同時,利用商品在不同城市中的差價賺回一點旅費。設 CCC 國 n 個城市的标号從 1 n1~ n1 n,阿龍決定從 11 1号城市出發,并最終在 nnn 号城市結束自己的旅行。在旅遊的過程中,任何城市可以重複經過多次,但不要求經過所有 nnn 個城市。阿龍通過這樣的貿易方式賺取旅費:他會選擇一個經過的城市買入他最喜歡的商品――水晶球,并在之後經過的另一個城市賣出這個水晶球,用賺取的差價當做旅費。由于阿龍主要是來 CCC 國旅遊,他決定這個貿易隻進行最多一次,當然,在賺不到差價的情況下他就無需進行貿易。
假設 CC C國有 555個大城市,城市的編号和道路連接配接情況如下圖,單向箭頭表示這條道路為單向通行,雙向箭頭表示這條道路為雙向通行。
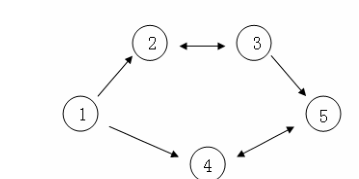
假設 1 n1~n1 n 号城市的水晶球價格分别為 4,3,5,6,14,3,5,6,14,3,5,6,1。
阿龍可以選擇如下一條線路:111->222->333->555,并在 22 2号城市以3 33 的價格買入水晶球,在 333号城市以5 5 5的價格賣出水晶球,賺取的旅費數為 2。
阿龍也可以選擇如下一條線路1 11->444->555->444->555,并在第11 1次到達5 55 号城市時以 11 1的價格買入水晶球,在第 222 次到達4 44 号城市時以6 66 的價格賣出水晶球,賺取的旅費數為5 55。
現在給出 nn n個城市的水晶球價格,mmm 條道路的資訊(每條道路所連接配接的兩個城市的編号以及該條道路的通行情況)。請你告訴阿龍,他最多能賺取多少旅費。
輸入格式
第一行包含 222 個正整數n n n和 mmm,中間用一個空格隔開,分别表示城市的數目和道路的數目。
第二行 n 個正整數,每兩個整數之間用一個空格隔開,按标号順序分别表示這 n 個城市的商品價格。
接下來 mmm 行,每行有3 3 3個正整數x,y,zx,y,zx,y,z,每兩個整數之間用一個空格隔開。如果 z=1z=1z=1,表示這條道路是城市x x x到城市y y y之間的單向道路;如果z=2 z=2z=2,表示這條道路為城市 xx x和城市yy y之間的雙向道路。
輸出格式
一 個整數,表示最多能賺取的旅費。如果沒有進行貿易,則輸出 000。
輸入輸出樣例
輸入 #1
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2 輸出 #1
5 說明/提示
【資料範圍】
輸入資料保證 111 号城市可以到達n n n号城市。
對于 10%的資料,1≤n≤61≤n≤61≤n≤6。
對于 30%的資料,1≤n≤1001≤n≤1001≤n≤100。
對于 50%的資料,不存在一條旅遊路線,可以從一個城市出發,再回到這個城市。
對于 100%的資料,1≤n≤1000001≤n≤1000001≤n≤100000,1≤m≤5000001≤m≤5000001≤m≤500000,1≤x1≤x1≤x,y≤ny≤ny≤n,1≤z≤21≤z≤21≤z≤2,1≤1≤1≤各城市
水晶球價格≤100≤100≤100。
NOIP 2009 提高組 第三題
将雙向邊存儲為兩條單向邊,建一張原圖一張反圖,跑兩邊dijkstra(或者spfa)。第一遍求數組d,d[x]表示從1到x的所有路徑中經過的權值最小的節點的權值。 第二遍求數組d1,d1[x]表示從n到x的所有路徑中經過的權值最大的節點的權值(由單源最短路的求法可知,隻能由确定的點n開始,是以必須建反圖求)。 然後周遊節點,ans=max(ans,d1[i]-d[i])更新答案。
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
const int M=1000005;
int head[N],ver[M],Next[M],d[N];bool v[N];
int head1[N],ver1[M],Next1[M],d1[N];bool v1[N];
int price[N];
int n,m,tot=0,tot1=0;
void add(int x,int y)
{
ver[++tot]=y;
Next[tot]=head[x];
head[x]=tot;
}
void add1(int x,int y)
{
ver1[++tot1]=y;
Next1[tot1]=head1[x];
head1[x]=tot1;
}
priority_queue< pair<int,int> >q;
priority_queue< pair<int,int> >q1;
void dij()
{
memset(d,0x3f,sizeof(d));
memset(v,0,sizeof(v));
d[1]=price[1];//一定要注意初始化!!!!!!!!! 千萬不能加v[1]=1;!!!!!!
q.push(make_pair(price[1],1));
while(q.size())
{
int x=q.top().second;q.pop();
if(v[x])continue;
v[x]=1;
int i;
for(i=head[x];i;i=Next[i])
{
int y=ver[i];
d[y]=min(d[x],price[y]);
q.push(make_pair(d[y],y));
}
}
}
void dij1()
{
memset(d1,-0x3f,sizeof(d1));//初始化為負無窮
memset(v1,0,sizeof(v1));
d1[n]=price[n];//v1[n]=1;//千萬不能加這一條
q1.push(make_pair(price[n],n));
while(q1.size())
{
int x=q1.top().second;q1.pop();
if(v1[x])continue;
v1[x]=1;
int i;
for(i=head1[x];i;i=Next1[i])
{
int y=ver1[i];
d1[y]=max(d1[x],price[y]);
q1.push(make_pair(d1[y],y));
}
}
}
int main()
{
cin>>n>>m;
int i;
for(i=1;i<=n;i++)
{
scanf("%d",&price[i]);
}
for(i=1;i<=m;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
if(z==1)
{
add(x,y);
add1(y,x);
}
else
{
add(x,y);add(y,x);
add1(x,y);add1(y,x);
}
}
dij();
dij1();
int ans=0;
for(i=1;i<=n;i++)
{
ans=max(ans,d1[i]-d[i]);
}
cout<<ans;
return 0;
}