核心考點:空間複雜度,fib了解,剪枝重複計算
大家都知道斐波那契數列,現在要求輸入一個正整數n,請你輸出斐波那契數列的第n項。
斐波那契數列是一個滿足
的數列。
解析一:(非常不提倡)
題目已經給出了斐波那契數列的狀态轉移方程,是以我們可以很容易使用遞歸的方式來求得第n個斐波那契數。
但如果使用遞歸來解決該問題,就不得不面對一個問題,那就是大量的重複計算,若是我們要得到第40個斐波那契數,那我們大緻需要經曆以下路徑。
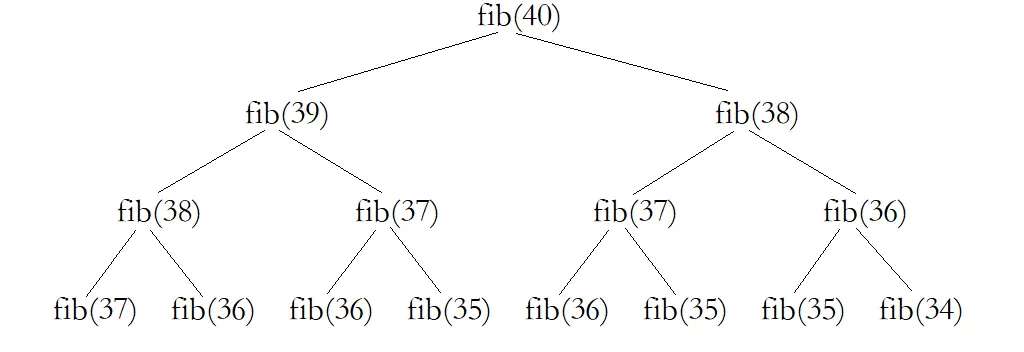
可以看到,圖中對于同一斐波那契數進行了多次計算,而且越往下對于同一斐波那契數的重複計算次數越多,是以并不提倡使用遞歸的方法解決該問題。
//遞歸
class Solution {
public:
int Fibonacci(int n) {
if (n == 1 || n == 2) //fib(1)=1, fib(2)=1
return 1;
return Fibonacci(n - 1) + Fibonacci(n - 2); //fib(n)=fib(n-1)+fib(n-2)
}
}; 解析二:(不提倡)
既然使用遞歸存在大量的重複計算,那麼我們可以考慮将已經計算過的斐波那契數儲存起來,這樣便避免了斐波那契數的重複計算。
例如,在計算第40個斐波那契數的中途需要計算第38個斐波那契數,而第38個斐波那契數已經被計算過了,那就無需再從此處遞歸下去了。
從圖中看來就是不用再計算二叉樹的某一枝葉了,是以該方法被形象的稱為“剪枝”。
将遞歸和剪枝配合起來使用,其時間複雜度相比單純的遞歸來說簡直快了太多了,但該方法也有一個弊端,那就是需要額外的記憶體空間來暫時儲存已經計算過的斐波那契數。
//遞歸+剪枝
class Solution {
private:
unordered_map<int, int> filter; //存儲已經計算過的斐波那契數
public:
int Fibonacci(int n) {
if (n == 1 || n == 2) //fib(1)=1, fib(2)=1
return 1;
int pper = 0; //第n-2個斐波那契數
if (filter.find(n - 2) == filter.end())
{
//在map當中沒有找到第n-2個斐波那契數,需要計算
pper = Fibonacci(n - 2);
filter.insert({ n - 2, pper });
}
else
{
//在map當中找到了第n-2個斐波那契數,直接擷取
pper = filter[n - 2];
}
int per = 0; //第n-1個斐波那契數
if (filter.find(n - 1) == filter.end())
{
//在map當中沒有找到第n-1個斐波那契數,需要計算
per = Fibonacci(n - 1);
filter.insert({ n - 1, per });
}
else
{
//在map當中找到了第n-1個斐波那契數,直接擷取
per = filter[n - 1];
}
return pper + per; //fib(n)=fib(n-1)+fib(n-2)
}
}; 解析三:(正解)
遞歸實際上是從終點看向起點,現在我們從起點看向終點,從第一個斐波那契數往後進行計算,需要第幾個斐波那契數就計算到第幾個。
而在該過程中我們不需要将所有計算過的斐波那契數全部儲存起來,因為一個斐波那契數的值隻與其前面兩個斐波那契數有關。
//動規
class Solution {
public:
int Fibonacci(int n) {
if (n == 1 || n == 2) //fib(1)=1, fib(2)=1
return 1;
int first = 1; //fib(1)=1
int second = 1; //fib(2)=1
int third = 0;
while (n > 2) //進行n-2次計算
{
//fib(n)=fib(n-1)+fib(n-2)
third = first + second;
first = second;
second = third;
n--;
}
return third;
}
};